Giải bài tập 5.37 trang 127 SGK Toán 9 tập 1 - Cùng khám phá

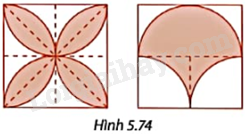
Đề bài

Trong Hình 5.74, độ dài cạnh của các hình vuông lớn là 10cm. Tính diện tích và chu vi của phần được tô màu.

Lời giải chi tiết

Đặt tên các điểm như hình vẽ.

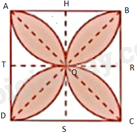
Độ dài mỗi cạnh của hình vuông nhỏ là: \(10:2 = 5cm\).

Ta thấy, diện tích bốn hình vuông nhỏ bằng nhau, 2 phần không được tô màu ở mỗi hình vuông nhỏ đều bằng nhau và diện tích mỗi cánh hoa đều bằng nhau.

Diện tích hình vuông AHOT là:

\({5^2} = 25\left( {c{m^2}} \right)\).

\(\frac{1}{4}\) diện tích hình tròn tâm T, bán kính 5cm là:

\(\frac{1}{4}{.5^2}.\pi  = \frac{{25\pi }}{4}\left( {c{m^2}} \right)\).

Diện tích phần không được tô màu trong hình vuông AHOT là:

\(2.\left( {25 - \frac{{25\pi }}{4}} \right)\left( {c{m^2}} \right)\).

Diện tích cánh hoa nằm trong hình vuông AHOT là:

\(25 - 2\left( {25 - \frac{{25\pi }}{4}} \right) =  - 25 + \frac{{25\pi }}{2}\left( {c{m^2}} \right)\).

Do đó, diện tích hình cần tính là: \(4.\left( { - 25 + \frac{{25\pi }}{2}} \right) =  - 100 + 50\pi \left( {c{m^2}} \right)\).

Hình trên gồm bốn cánh hoa, trong đó:

+ Hai cánh nằm trong hình chữ nhật AHSD gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.

+ Hai cánh nằm trong hình chữ nhật HSCB gồm 4 cung, mỗi cung là một phần tư đường tròn bán kính 5cm.

Do đó, chu vi của hình tô màu bằng 2 lần chu vi đường tròn bán kính 5cm, tức là: \(2.2.5\pi  = 20\pi \left( {cm} \right)\)

Hình vẽ thứ hai:

Hình gồm hai cung: Một cung là một nửa đường tròn có bán kính 5cm, hai cung mỗi cung là một phần tư đường tròn bán kính 5cm nên chu vi hình bằng chu vi đường tròn bán kính 5cm.

Vậy chu vi hình vẽ là: \(2\pi .5 = 10\pi \left( {cm} \right)\)

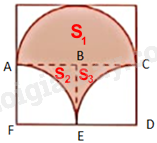
Đặt tên các điểm như hình vẽ.

Diện tích nửa hình tròn bán kính 5cm là:

\({S_1} = {5^2}\pi  = 25\pi \left( {c{m^2}} \right)\).

Diện tích hình vuông BCDE là:

\({S_{BCDE}} = {5^2} = 25\left( {c{m^2}} \right)\)

Phần không tô màu trong hình vuông BCDE là một phần tư hình tròn bán kính 5cm nên diện tích phần không tô màu trong hình vuông BCDE là:

\(S = \frac{1}{4}{.5^2}\pi  = \frac{{25\pi }}{4}\left( {c{m^2}} \right)\).

Diện tích phần tô màu trong hình vuông BCDE là:

\({S_2} = {S_{BCDE}} - S = 25\pi  - \frac{{25}}{4}\pi  = \frac{{75\pi }}{4}\left( {c{m^2}} \right)\).

Tương tự ta có, diện tích phần tô màu trong hình vuông ABEF là:

\({S_3} = \frac{{75\pi }}{4}\left( {c{m^2}} \right)\).

Vậy diện tích phần tô màu là:

\({S_1} + {S_2} + {S_3} = 25\pi  + \frac{{75\pi }}{4} + \frac{{75\pi }}{4} = \frac{{125\pi }}{2}\left( {c{m^2}} \right)\).