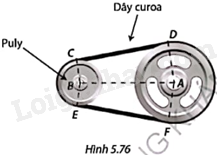
Giải bài tập 5.39 trang 128 SGK Toán 9 tập 1 - Cùng khám pháTrong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là (AB = 30cm). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính: a) Độ dài CD và số đo các góc của tứ giác ABCD; b) Độ dài dây curoa. Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút. Quảng cáo
Đề bài Trong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là \(AB = 30cm\). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính: a) Độ dài CD và số đo các góc của tứ giác ABCD; b) Độ dài dây curoa. Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút.
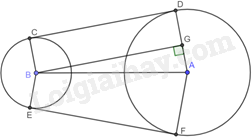
Phương pháp giải - Xem chi tiết a) + Kẻ BG vuông góc với AD tại G. + Chứng minh tứ giác BCDG là hình chữ nhật suy ra \(CD = BG\), \(BC = DG\) + Áp dụng định lí Pythagore vào tam giác ABG vuông tại G để tính BG, AG; tính cos GAB, từ đó tính góc GAB. + Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\), từ đó tính được góc ABC. b) + Tính số đo cung lớn FD, số đo cung nhỏ CE. + Tính độ dài cung lớn FD, độ dài cung nhỏ CE. + Độ dài dây curoa là: \({l_{DF}} + {l_{CE}} + CD + EF\). Lời giải chi tiết
Kẻ BG vuông góc với AD tại G. Suy ra: \(\widehat {BGD} = \widehat {BGA} = {90^o}\). Vì CD là tiếp tuyến của hai đường tròn (B) và (A) nên \(BC \bot CD,CD \bot AD\) nên \(\widehat {BCD} = \widehat {CDG} = {90^o}\). Tứ giác BGDC có: \(\widehat {BCD} = \widehat {CDG} = \widehat {BGD} = {90^o}\) nên tứ giác BGDC là hình chữ nhật. Do đó, \(CD = BG\), \(BC = DG = 7cm\). Tam giác BGA vuông tại G nên: + \(\cos GAB = \frac{{GA}}{{AB}} = \frac{{DA - GD}}{{AB}} = \frac{{5,5}}{{30}} = \frac{{11}}{{60}}\) nên \(\widehat {GAB} \approx {79^o}26'\) + \(B{G^2} + G{A^2} = A{B^2}\), \(BG = \sqrt {A{B^2} - {{\left( {AD - DG} \right)}^2}} = \sqrt {{{30}^2} - {{\left( {12,5 - 7} \right)}^2}} = \frac{{7\sqrt {71} }}{2}\left( {cm} \right)\) nên \(CD = \frac{{7\sqrt {71} }}{2}cm\) Chứng minh tương tự ta có: \(EF = \frac{{7\sqrt {71} }}{2}cm\) Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\) \(\widehat {ABC} = {360^o} - \left( {\widehat C + \widehat D + \widehat {DAB}} \right) \approx {360^o} - \left( {{{90}^o} + {{90}^o} + {{79}^o}26'} \right) \approx {100^o}34'\) b) Chứng minh tương tự phần a ta có: \(\widehat {FAB} \approx {79^o}26'\), \(\widehat {EBF} \approx {100^o}34'\) Do đó, \(\widehat {DAF} = \widehat {DAB} + \widehat {FAB} \approx {158^o}52'\). Do đó, số đo cung nhỏ DF là: \({158^o}52'\). Suy ra, số đo cung lớn DF là: \({360^o} - {158^o}52' = {201^o}8'\) Số đo cung CE nhỏ là: \({158^o}52'\). Độ dài cung lớn DF là: \({l_{DF}} = \frac{{\pi {{.12.201}^o}8'}}{{{{180}^o}}} = \frac{{3017\pi }}{{225}}\left( {cm} \right)\) Độ dài cung nhỏ CE là: \({l_{CE}} = \frac{{\pi .7,{{5.158}^o}52'}}{{180}} = \frac{{2383\pi }}{{360}}\left( {cm} \right)\) Độ dài dây curoa là: \({l_{DF}} + {l_{CE}} + CD + EF \approx \frac{{3017\pi }}{{225}} + \frac{{2383\pi }}{{360}} + 2.\frac{{7\sqrt {71} }}{2} \approx 121,9\left( {cm} \right)\)
|




















Danh sách bình luận