Giải bài tập 4.20 trang 89 SGK Toán 9 tập 1 - Cùng khám pháLàm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Người ta làm một con đường gồm ba đoạn AB, BC, CD bao quanh hồ nước như Hình 4.34. Tính khoảng cách AD. Gợi ý: Từ điểm A, kẻ đường vuông góc AH xuống BC và AK xuống CD. Quảng cáo
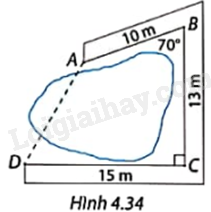
Đề bài Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Người ta làm một con đường gồm ba đoạn AB, BC, CD bao quanh hồ nước như Hình 4.34. Tính khoảng cách AD. Gợi ý: Từ điểm A, kẻ đường vuông góc AH xuống BC và AK xuống CD.
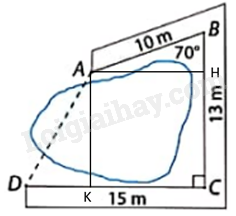
Phương pháp giải - Xem chi tiết + Từ điểm A, kẻ đường thẳng vuông góc BC tại H và vuông góc với CD tại K. + Tam giác AHB vuông tại H nên \(BH = AB.\cos B\), \(AH = AB.\sin B\). + Do đó, \(CH = BC - BH\). + Chứng minh tứ giác AHCK là hình chữ nhật suy ra \(AH = KC,AK = CH\). + Ta có: \(DK = DC - KC\). + Áp dụng định lí Pythagore vào tam giác ADK vuông tại K tính được AD. Lời giải chi tiết
Từ điểm A, kẻ đường thẳng vuông góc BC tại H và vuông góc với CD tại K. Tam giác AHB vuông tại H nên \(BH = AB.\cos B = 10\cos {70^o}\left( m \right)\), \(AH = AB.\sin B = 10\sin {70^o}\left( m \right)\). Do đó, \(CH = BC - BH = 13 - 10\cos {70^o} \approx 9,6\left( m \right)\). Tứ giác AHCK có \(\widehat {AHC} = \widehat {HCK} = \widehat {AKC} = {90^o}\) nên tứ giác AHCK là hình chữ nhật. Do đó, \(AH = KC = 10\sin {70^o}\left( m \right)\), \(AK = CH \approx 9,6m\) Ta có: \(DK = DC - KC = 15 - 10\sin {70^o} \approx 5,6m\) Tam giác ADK vuông tại K nên \(D{A^2} = A{K^2} + D{K^2} = 9,{6^2} + 5,{6^2} = 123,52\) (định lí Pythagore) nên \(AD \approx 11,1m\).
|




















Danh sách bình luận