Giải bài 7 trang 87 SGK Toán 10 tập 1 – Cánh diều

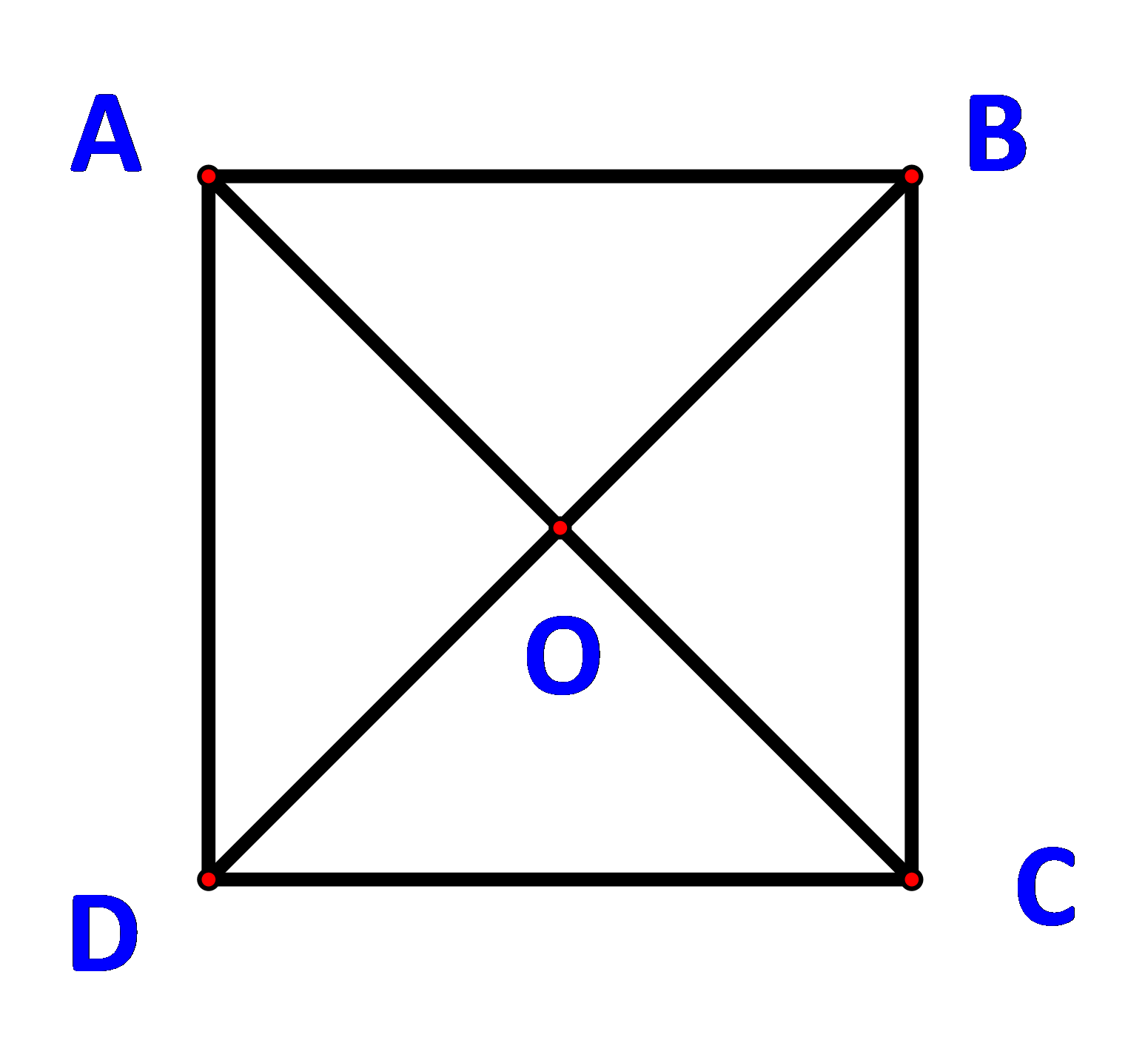
Đề bài

Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:

a) $\overrightarrow {DA}  + \overrightarrow {DC}$

b) $\overrightarrow {AB}  - \overrightarrow {AD}$

c) $\overrightarrow {OA}  + \overrightarrow {OB}$ với O là giao điểm của AC và BD.

Lời giải chi tiết

 

a) Do ABCD cũng là một hình bình hành nên $\overrightarrow {DA}  + \overrightarrow {DC}  = \overrightarrow {DB}$

$\Rightarrow \;|\overrightarrow {DA}  + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2$

b) Ta có: $\overrightarrow {AD}  + \overrightarrow {DB}  = \overrightarrow {AB}$ $\Rightarrow \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB}$

$\Rightarrow \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2$

c) Ta có: $\overrightarrow {DO}  = \overrightarrow {OB}$

$\Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {DO}  = \overrightarrow {DO}  + \overrightarrow {OA}  = \overrightarrow {DA}$

$\Rightarrow \left| {\overrightarrow {OA}  + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.$