Bài 2.3 phần bài tập bổ sung trang 82 SBT toán 8 tập 1

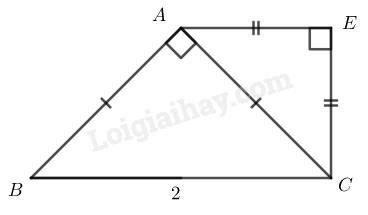
Đề bài

Cho tam giác \(ABC\) vuông cân tại \(A,\) \(BC= 2 cm.\) Ở phía ngoài tam giác \(ABC,\) vẽ tam giác \(ACE\) vuông cân tại \(E.\)

\(a)\) Chứng minh rằng \(AECB\) là hình thang vuông

\(b)\) Tính các góc và các cạnh của hình thang \(AECB.\)

Lời giải chi tiết

\(a)\) \(∆ ABC\) vuông cân tại \(A\)

\(\Rightarrow \widehat {ACB} = {45^0}\)

\(∆ EAC\) vuông cân tại \(E\)

\( \Rightarrow \widehat {EAC} = {45^0}\) 

Suy ra: \(\widehat {EAC} = \widehat {ACB}\)

\(⇒ AE // BC\) (vì có cặp góc ở vị trí so le trong bằng nhau)

nên tứ giác \(AECB\) là hình thang có \(\widehat E = {90^0}\). Vậy \(AECB\) là hình thang vuông

\( b)\) \(\widehat E = \widehat {ECB} = {90^0},\widehat B = {45^0}\)

Vì \(AE // BC\) nên \(\widehat B + \widehat {EAB} = {180^0}\) (hai góc trong cùng phía bù nhau)

\( \Rightarrow \widehat {EAB} = {180^0} - \widehat B\)\( = {180^0} - {45^0} = {135^0}\)

\(∆ ABC\) vuông tại \(A.\) Theo định lí Py-ta-go ta có:

\(A{B^2} + A{C^2} = B{C^2}\)  mà \(AB= AC \;\;(gt)\)

\(\Rightarrow 2A{B^2} = B{C^2} = {2^2} = 4 \) 
\( A{B^2} = 2 \Rightarrow AB = \sqrt 2 (cm) \)

\(\Rightarrow AC = \sqrt 2 (cm) \) 

\(∆ AEC\) vuông tại \(E.\) Theo định lí Py-ta-go ta có:

\(E{A^2} + E{C^2} = A{C^2}\), mà \(EA = EC\;\;\; (gt)\)

\(\eqalign{
& \Rightarrow 2E{A^2} = A{C^2} = 2 \cr 
& \Rightarrow E{A^2} = 1 \cr 
& \Rightarrow EA = 1(cm) \Rightarrow EC = 1(cm) \cr} \)

Loigiaihay.com