Bài 21 trang 158 SBT toán 8 tập 1

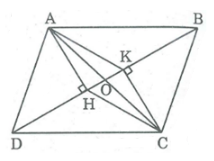
Đề bài

Cho hình bình hành \(ABCD\) \((h. 183).\) Từ \(A\) và \( C\) kẻ \(AH\) và \(CK\) vuông góc với đường chéo \(BD.\) Chứng minh rằng hai đa giác \(ABCH\) và \(ADCK\) có cùng diện tích.

Lời giải chi tiết

Xét \(∆ ABC\) và \(∆ CDA\) có: 

\(AC\) chung

\(AB = CD\) (Vì \(ABCD\) là hình bình hành)

\(BC = DA\) (Vì \(ABCD\) là hình bình hành)

Suy ra \(∆ ABC = ∆ CDA \,(c.c.c)\)

\( \Rightarrow {S_{ABC}} = {S_{CDA}}\)     \((1)\)

Gọi O là giao điểm của hai đường chéo AC và BD.

\(ABCD\) là hình bình hành nên \(OA = OC\) (tính chất hình bình hành)

Xét hai tam giác vuông \(AOH\) và \(CKO\) có:

\(OA = OC\) (cmt)

\(\widehat {AOH} = \widehat {COK}\) (đối đỉnh)

\( \Rightarrow \Delta AOH = \Delta COK\) (cạnh huyền-góc nhọn)

\( \Rightarrow AH = CK\) (hai cạnh tương ứng)

Mặt khác: \(AH,\, CK\) cùng vuông góc với \(BD\) nên \(AH // CK\)

Tứ giác \(AHCK\) có \(AH = CK\) (cmt) và \(AH //CK\) (cmt) nên \(AHCK\) là hình bình hành. 

Do đó: \(AK = CH\) (tính chất hình bình hành)

Xét \(∆ AHC\) và \(∆ CKA\) có:

\(AC\) chung

\(CH = AK\) (cmt)

\(AH = CK\) (cmt)

\( \Rightarrow \) \(∆ AHC = ∆ CKA \,(c.c.c)\)

\( \Rightarrow {S_{AHC}} = {S_{CKA}}\)    \((2)\)

Từ \((1)\) và \((2)\) suy ra:

\({S_{ABC}} + {S_{AHC}} = {S_{CDA}} + {S_{CKA}}\)

Hay \({S_{ABCH}} = {S_{ADCK}}\)

Loigiaihay.com