Bài 159 trang 100 SBT Toán 8 tập 1Giải bài 159 trang 100 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.... Quảng cáo
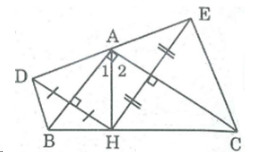
Đề bài Cho tam giác ABC vuông tại A, đường cao AH. Gọi b. Tam giác DHE là tam giác gì ? Vì sao ? c. Tứ giác BDEC là hình gì ? Vì sao ? d. Chứng minh rằng BC = BD + CE. Phương pháp giải - Xem chi tiết Nhẩm lại dấu hiệu nhận biết của các tứ giác đã học rồi chứng minh. Hình thang có 1 góc vuông là hình thang vuông Trong một tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông Lời giải chi tiết
a) Điểm D đối xứng điểm H qua trục AB ⇒ AB là đường trung trực của HD ⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A Suy ra: AB là tia phân giác của \(\widehat {DAH} \Rightarrow \widehat {DAB} = {\widehat A_1}\) Điểm H và điểm E đối xứng qua trục AC ⇒ AC là đường trung trực của HE ⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A Suy ra: AC là đường phân giác của \(\widehat {HAE} \Rightarrow {\widehat A_2} = \widehat {EAC}\) Ta có: \(\widehat {DAE} = \widehat {DAH} + \widehat {HAE}\)\( = 2\left( {{{\widehat A}_1} + {{\widehat A}_2}} \right) = {2.90^0} = {180^0}\) Suy ra D, A, E thẳng hàng Lại có: AD = AE (vì cùng bằng AH) Nên điểm A là trung điểm của đoạn DE Vậy điểm D đối xứng với điểm E qua điểm A. b) Tam giác DHE có HA là trung tuyến và \(AH =AD=AE= \displaystyle {1 \over 2}DE\) nên tam giác DHE vuông tại H. c) Xét \(\Delta ADB\) và \( \Delta AHB\) có: +) AB chung +) BD = BH ( vì AB là trung trực của DH) +) AD = AH (vì AB là trung trực của DH) \(\Rightarrow \Delta ADB = \Delta AHB\;(c.c.c)\) \( \Rightarrow \widehat {AHB} = \widehat {ADB}=90^0\) (hai góc tương ứng) \(⇒ BD ⊥ DE\) Xét \(\Delta AEC\) và \( \Delta AHC\) có: +) AC chung +) EC = HC ( vì AC là trung trực của EH) +) AE = AH (vì AC là trung trực của EH) \(\Rightarrow \Delta AEC = \Delta AHC\;(c.c.c)\) \( \Rightarrow \widehat {AHC} = \widehat {AEC}=90^0\) (hai góc tương ứng) \(⇒ EC ⊥ DE \) Suy ra BD//CE (vì cùng vuông góc với DE) d) Do AB là đường trung trực của DH nên BD=BH (5) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
