Bài 153 trang 99 SBT Toán 8 tập 1

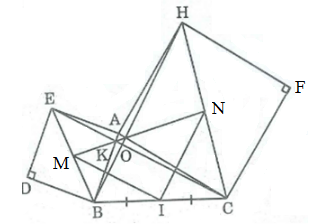
Đề bài

Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.

a. Chứng minh rằng EC = BH, EC ⊥ BH.

b. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?

Lời giải chi tiết

a. Ta có: \(\widehat {BAH} = \widehat {BAC} + \widehat {CAH} = \widehat {BAC} + {90^0}\)

\(\widehat {EAC} = \widehat {BAC} + \widehat {BAE} = \widehat {BAC} + {90^0}\)

Suy ra: \(\widehat {BAH} = \widehat {EAC}\)

- Xét ∆ BAH và ∆ EAC:

BA = EA (vì ABDE là hình vuông)

\(\widehat {BAH} = \widehat {EAC}\) (chứng minh trên)

AH = AC (vì ACFH là hình vuông)

Do đó: \(∆ BAH = ∆ EAC\) (c.g.c)

⇒ BH = EC

Gọi giao điểm của EC với AB và BH lần lượt là K và O.

\(\widehat {AEC} = \widehat {ABH}\) (vì \(∆ BAH = ∆ EAC)\) (1)

hay \(\widehat {AEK} = \widehat {OBK}\)

- Trong ∆ AEK ta có: \(\widehat {EAK} = {90^0}\)

\( \Rightarrow \widehat {AEK} + \widehat {AKE} = {90^0}\) (2)

\(\widehat {AKE} = \widehat {OKB}\) (đối đỉnh) (3)

Từ (1), (2) và (3) suy ra: \(\widehat {OKB} + \widehat {OBK} = {90^0}\)

- Trong ∆ BOK ta có: \(\widehat {BOK} + \widehat {OKB} + \widehat {OBK} = {180^0}\)

\( \Rightarrow \widehat {BOK} = {180^0} - \left( {\widehat {OKB} + \widehat {OBK}} \right)\)\( = {180^0} - {90^0} = {90^0}\)

Suy ra: EC ⊥ BH

b. Trong ∆ EBC ta có:

M là trung điểm của EB (tính chất hình vuông)

I là trung điểm của BC (gt)

nên MI là đường trung bình của tam giác EBC

⇒ MI = \(\displaystyle {1 \over 2}\)EC và MI // EC (tính chất đường trung bình của tam giác)

- Trong ∆ BCH ta có:

I là trung điểm của BC (gt)

N là trung điểm của CH (tính chất hình vuông)

nên NI là đường trung bình của ∆ BCH

⇒ NI = \(\displaystyle {1 \over 2}\)BH và NI // BH (tính chất đường trung bình của tam giác)

BH = CE (chứng minh trên)

Suy ra: MI = NI nên ∆ INM cân tại I

MI // EC (chứng minh trên)

EC ⊥ BH (chứng minh trên)

Suy ra: MI ⊥ BH

Mà NI // BH (chứng minh trên)

Suy ra: MI ⊥ NI hay \(\widehat {MIN} = {90^0}\)

Vậy ∆ IMN vuông cân tại I.

Loigiaihay.com