Bài 12.2 phần bài tập bổ sung trang 99 SBT Toán 8 tập 1

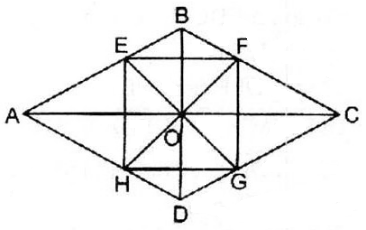
Đề bài

Cho hình thoi \(ABCD,\) \(O\) là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh \(O\) cắt các cạnh \(AB,\, BC,\, CD,\, DA\) theo thứ tự ở \(E,\, F,\, G,\, H.\) Tứ giác \(EFGH\) là hình gì?

Lời giải chi tiết

Ta có: \(\widehat {AOB}\) và \(\widehat {COD}\) đối đỉnh nên \(E,\, O,\, G\) thẳng hàng

\(\widehat {BOC}\) và \(\widehat {AOD}\) đối đỉnh nên \(F,\, O,\, H\) thẳng hàng

Xét \(∆ BEO\) và \(∆ BFO:\)

\(\widehat {EBO} = \widehat {FBO}\) (tính chất hình thoi)

\(OB\) cạnh chung

\(\widehat {EOB} = \widehat {FOB} = {45^0}\) (tính chất tia phân giác của các góc vuông)

Do đó: \(∆ BEO = ∆ BFO\, (g.c.g)\)

\(⇒ OE = OF\) (1)

Xét \(∆ BEO\) và \(∆ DGO:\)

\(\widehat {EBO} = \widehat {GDO}\) (so le trong)

\(OB = OD\) (tính chất hình thoi)

\(\widehat {EOB} = \widehat {GOD}\) (đối đỉnh)

Do đó: \(∆ BEO = ∆ DGO\, (g.c.g)\)

\(⇒ OE = OG\) (2)

Xét \(∆ AEO\) và \(∆ AHO:\)

\(\widehat {EAO} = \widehat {HAO}\) (tính chất hình thoi)

\(OA\) cạnh chung

\(\widehat {EOA} = \widehat {HOA} = {45^0}\) (tính chất tia phân giác của các góc vuông)

Do đó: \(∆ AEO = ∆ AHO\, (g.c.g)\)

\(⇒ OE = OH\) (3)

Từ (1), (2) và (3) suy ra: \(OE = OF = OG = OH\) hay \(EG = FH\)

nên tứ giác \(EFGH\) là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)

Lại có OE và OF là hai tia phân giác của hai góc kề bù \(\widehat {AOB},\widehat {BOC}\) nên \(OE ⊥ OF\) (tính chất tia phân giác của hai góc kề bù)

hay \(EG ⊥ FH\)

Vậy hình chữ nhật \(EFGH\) là hình vuông.

Loigiaihay.com