Giải bài 1 trang 99 SGK Toán 10 tập 1 – Cánh diều

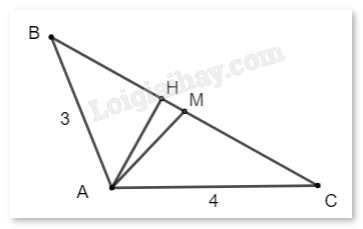
Đề bài

Cho tam giác ABC có $AB = 3,AC = 4,\widehat {BAC} = {120^o}.$ Tính (làm tròn kết quả đến hàng đơn vị):

a) Độ dài cạnh BC và độ lớn góc B.

b) Bán kính đường tròn ngoại tiếp

c) Diện tích của tam giác

d) Độ dài đường cao xuất phát từ A

e) $\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC}$ với M là trung điểm của BC.

Lời giải chi tiết

a) Áp dụng định lí cosin trong tam giác ABC, ta có:

$\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} - 2.3.4.\cos {120^o}\\ \Leftrightarrow B{C^2} = 37\\ \Leftrightarrow BC \approx 6\end{array}$

Áp dụng định lí sin trong tam giác ABC, ta có:

 $\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{4.\sin {{120}^o}}}{6} = \frac{{\sqrt 3 }}{3}\\ \Leftrightarrow \widehat B \approx {35^o}\end{array}$

b) $R = \frac{{BC}}{{2.\sin A}} = \frac{6}{{2.\sin {{120}^o}}} = 2\sqrt 3$

c) Diện tích tam giác ABC: $S = \frac{1}{2}4.3.\sin {120^o} = 3\sqrt 3 .$

d) Gọi H là chân đường cao hạ từ đỉnh A.

Ta có: $S = \frac{1}{2}AH.BC$

$\Rightarrow AH = \frac{{2S}}{{BC}} = \frac{{2.3\sqrt 3 }}{6} = \sqrt 3$

e) $\overrightarrow {AB} .\overrightarrow {AC}  = 3.4.\cos (\widehat {BAC}) = 12.\cos {120^o} =  - 6.$

Ta có: $\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM}$ (do M là trung điểm BC)

$\Leftrightarrow \overrightarrow {AM}  = \frac{1}{2}(\overrightarrow {AB}  + \overrightarrow {AC} )$

$\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC}  = \frac{1}{2}(\overrightarrow {AB}  + \overrightarrow {AC} )(\overrightarrow {AC}  - \overrightarrow {AB} )\\ = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\\ = \frac{1}{2}\left( {{4^2} - {3^2}} \right) = \frac{7}{2}.\end{array}$