Đề kiểm tra giữa học kì 1 Toán 8 - Đề số 1Đề bài
Câu 1 :
Chọn câu đúng.
Câu 2 :
Biểu thức \(E = {x^2} - 20x + 101\) đạt giá trị nhỏ nhất khi
Câu 3 :
Chọn câu đúng.
Câu 4 :
Cho \({x^2} + ax + x + a = \left( {x + a} \right).\left( {...} \right)\) Biểu thức thích hợp điền vào dấu \(...\) là
Câu 5 :
Ta có \((x + 2)(x + 3)(x + 4)(x + 5) - 24 = \left( {{x^2} + 7x + a} \right)\left( {{x^2} + 7x + b} \right)\) với \(a,\,b\) là các số nguyên và \(a < b\) . Khi đó \(a - b\) bằng
Câu 6 :
Chia đơn thức \({\left( { - 3x} \right)^5}\) cho đơn thức \({\left( { - 3x} \right)^2}\) ta được kết quả là
Câu 7 :
Thương của phép chia \(\left( {9{x^4}{y^3} - 18{x^5}{y^4} - 81{x^6}{y^5}} \right):\left( { - 9{x^3}{y^3}} \right)\) là đa thức có bậc là:
Câu 8 :
Biết phần dư của phép chia đa thức \(\left( {{x^5} + {x^3} + {x^2} + 2} \right)\) cho đa thức \(\left( {{x^3} + 1} \right)\) là số tự nhiên \(a\) . Chọn câu đúng.
Câu 9 :
Hãy chọn câu sai
Câu 10 :
Tính độ dài đường trung bình của hình thang cân, biết rằng hai đường chéo vuông góc với nhau và đường cao của nó bằng $10cm$ .
Câu 11 :
Hãy chọn câu đúng. Tứ giác $ABCD$ là hình bình hành nếu.
Câu 12 :
Cho hình bình hành $ABCD$ . Gọi $I,{\rm{ }}K$ theo thứ tự là trung điểm của $CD,{\rm{ }}AB$ . Đường chéo $BD$ cắt $AI,{\rm{ }}CK$ theo thứ tự ở $E,{\rm{ }}F$ . Chọn khẳng định đúng.
Câu 13 :
Cho tứ giác \(ABCD\), lấy \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA.\) Tứ giác \(ABCD\) cần có điều kiện gì để \(MNPQ\) là hình chữ nhật.
Câu 14 :
Cho tam giác $ABC,$ đường cao $AH$ . Gọi $I$ là trung điểm của $AC,E$ là điểm đối xứng với $H$ qua $I$. Tứ giác $AECH$ là hình gì?
Câu 15 :
Cho hình chữ nhật $ABCD$ có \(AB = a;\,AD = b\) . Cho $M$ , $N$ , $P$ , $Q$ là các đỉnh của tứ giác $MNPQ$ và lần lượt thuộc các cạnh $AB$ , $BC$ ,$CD,DA$ . Tìm giá trị nhỏ nhất của chu vi tứ giác $MNPQ$ .
Câu 16 :
Hình thoi không có tính chất nào dưới đây?
Câu 17 :
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
Câu 18 :
Cho hình vuông $ABCD$ . Trên các cạnh $AB,BC,CD,DA$ lần lượt lấy các điểm $E,F,G,H$ sao cho $AE = BF = CG = DH$ . Tứ giác \(EFGH\) là hình gì?
Câu 19 :
Cho hình vuông có chu vi \(28\,cm\) . Độ dài cạnh hình vuông là:
Câu 20 :
Cho $B = {\left( {{x^2} + 3} \right)^2} - {x^2}\left( {{x^2} + 3} \right) - 3\left( {x + 1} \right)\left( {x - 1} \right)$. Chọn câu đúng.
Câu 21 :
Tìm giá trị \(x\) thỏa mãn \(2x\left( {x - 3} \right) - \left( {3 - x} \right) = 0\)
Câu 22 :
Thu gọn biểu thức \(\dfrac{1}{9}{x^2}{y^3}:{\left( { - 3xy} \right)^2}\) ta được
Câu 23 :
Chọn câu sai.
Câu 24 :
So sánh \(A = 2019.2021.a\) và \(B = \left( {{{2019}^2} + 2.2019 + 1} \right).a\) (với \(a > 0\))
Câu 25 :
Viết biểu thức \(\left( {\dfrac{y}{2} + 6} \right)\left( {\dfrac{{{y^2}}}{4} - 3y + 36} \right)\) dưới dạng tổng hai lập phương
Câu 26 :
Cho \({\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)\). Khi đó
Câu 27 :
Cho \(27{x^3} - 0,001 = \left( {3x - 0,1} \right)\left( {...} \right)\) . Biểu thức thích hợp điền vào dấu \(...\) là
Câu 28 :
Cho \({x^6} - 1 = \left( {x + A} \right)\left( {x + B} \right)\left( {{x^4} + {x^2} + C} \right)\), biết \(A,\,B,C\) là các số nguyên. Khi đó \(A + B + C\) bằng
Câu 29 :
Cho \({x^2} - 4xy + 4{y^2} - 4 = \left( {x - my + 2} \right)\left( {x - 2y - 2} \right)\) với \(m \in \mathbb{R}\) . Chọn câu đúng
Câu 30 :
Tính giá trị của biểu thức \(B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\) khi \({x^3} - x = 6\)
Câu 31 :
Phân tích đa thức \(A = ab\left( {a + b} \right) - bc\left( {b + c} \right) - ac\left( {c - a} \right)\) thành nhân tử ta được
Câu 32 :
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
Lời giải và đáp án
Câu 1 :
Chọn câu đúng.
Đáp án : C Phương pháp giải :
Sử dụng quy tắc nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau: \(\left( {A + B} \right)\left( {C + D} \right) = AC + AD + BC + BD\) Lời giải chi tiết :
Ta có $\left( {{x^2} - 1} \right)\left( {{x^2} + 2x} \right) $$= {x^2}.{x^2} + {x^2}.2x - 1.{x^2} - 1.2x $$= {x^4} + 2{x^3} - {x^2} - 2x$ Chú ý
Một số em có thể nhân thiếu hạng tử \( - 1.{x^2}\) dẫn đến chọn D sai, hoặc thiếu \({x^2}.2x\) dẫn đến chọn B sai.
Câu 2 :
Biểu thức \(E = {x^2} - 20x + 101\) đạt giá trị nhỏ nhất khi
Đáp án : B Phương pháp giải :
Biến đổi \(E\) về dạng \({\left( {A - B} \right)^2} + m\) rồi đánh giá \({\left( {A - B} \right)^2} + m \ge m\) . Dấu “=” xảy ra khi \(A = B\) Giá trị nhỏ nhất của \(E\) là \(m\) khi \(A = B\) Lời giải chi tiết :
Ta có \(E = {x^2} - 20x + 101 = {x^2} - 2.x.10 + 100 + 1 = {\left( {x - 10} \right)^2} + 1\) Vì \({\left( {x - 10} \right)^2} \ge 0;\,\forall x\)\( \Rightarrow {\left( {x - 10} \right)^2} + 1 \ge 1.\) Dấu “=” xảy ra khi \({\left( {x - 10} \right)^2} = 0 \)\(\Leftrightarrow x - 10 = 0 \Leftrightarrow x = 10\) Vậy giá trị nhỏ nhất của \(E\) là \(1\) khi \(x = 10.\) Chú ý
Các em có thể thay lần lượt từng đáp án vào biểu thức \(E\) rồi nhận giá trị nhỏ nhất thu được. Tuy nhiên cách làm này không giúp các em hiểu rõ bản chất bài toán, chỉ phù hợp để làm trắc nghiệm.
Câu 3 :
Chọn câu đúng.
Đáp án : A Lời giải chi tiết :
Ta có \({\left( {A + B} \right)^3} \)\( = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) nên phương án C sai, A đúng. \({\left( {A - B} \right)^3} \)\( = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) nên phương án B sai, D sai Chú ý
Một số em có thể nhớ nhầm công thức dẫn đến chọn đáp án sai.
Câu 4 :
Cho \({x^2} + ax + x + a = \left( {x + a} \right).\left( {...} \right)\) Biểu thức thích hợp điền vào dấu \(...\) là
Đáp án : A Lời giải chi tiết :
Ta có \({x^2} + ax + x + a \)\( = \left( {{x^2} + x} \right) + \left( {ax + a} \right) \)\( = x\left( {x + 1} \right) + a\left( {x + 1} \right) \)\( = \left( {x + a} \right)\left( {x + 1} \right)\) Chú ý
Các em có thể nhóm theo cách khác \({x^2} + ax + x + a \)\( = \left( {{x^2} + ax} \right) + \left( {x + a} \right) \)\( = x\left( {x + a} \right) + \left( {x + a} \right) \)\( = \left( {x + a} \right)\left( {x + 1} \right)\)
Câu 5 :
Ta có \((x + 2)(x + 3)(x + 4)(x + 5) - 24 = \left( {{x^2} + 7x + a} \right)\left( {{x^2} + 7x + b} \right)\) với \(a,\,b\) là các số nguyên và \(a < b\) . Khi đó \(a - b\) bằng
Đáp án : D Phương pháp giải :
Sử dụng phương pháp đặt ẩn phụ sau đó dùng hằng đẳng thức để phân tích đa thức vế trái thành nhân tử. + Nhân hai hạng tử $(x+2)(x+5)$; $(x+3)(x+4)$ + Đặt \({x^2} + 7x + 11 = t\) + Phân tích biểu thức ẩn $t$ thu được + Thay trở lại \(t={x^2} + 7x + 11\) ta thu được tích các nhân tử cần tìm từ đó suy ra $a,b.$ Lời giải chi tiết :
Ta có \(T = (x + 2)(x + 3)(x + 4)(x + 5) - 24\)\( = \left[ {\left( {x + 2} \right)\left( {x + 5} \right)} \right].\left[ {\left( {x + 3} \right)\left( {x + 4} \right)} \right] - 24\)\( = \left( {{x^2} + 7x + 10} \right).\left( {{x^2} + 7x + 12} \right) - 24\) Đặt \({x^2} + 7x + 11 = t\), ta được \(T = \left( {t - 1} \right)\left( {t + 1} \right) - 24 = {t^2} - 1 - 24 = {t^2} - 25 = \left( {t - 5} \right)\left( {t + 5} \right)\) Thay \(t={x^2} + 7x + 11 \), ta được \( T= \left( {t - 5} \right)\left( {t + 5} \right)= \left( {{x^2} + 7x + 11 - 5} \right)\left( {{x^2} + 7x + 11 + 5} \right)\)\( = \left( {{x^2} + 7x + 6} \right)\left( {{x^2} + 7x + 16} \right)\) Suy ra \(a = 6;b = 16\, \Rightarrow a - b = - 10\) Chú ý
Một số em có thể không để ý đến điều kiện \(a < b\) nên tính sai hiệu \(a - b\) .
Câu 6 :
Chia đơn thức \({\left( { - 3x} \right)^5}\) cho đơn thức \({\left( { - 3x} \right)^2}\) ta được kết quả là
Đáp án : D Phương pháp giải :
* Sử dụng quy tắc chia đơn thức cho đơn thức. Muốn chia đơn thức \(A\) cho đơn thức \(B\) (trong trường hợp \(A\) chia hết cho \(B\) ) ta làm như sau: + Chia hệ số của đơn thức \(A\) cho hệ số của đơn thức \(B\) + Chia lũy thừa của từng biến trong \(A\) cho lũy thừa của cùng biến đó trong \(B\) . + Nhân các kết quả vừa tìm được với nhau. * Sử dụng công thức chia hai lũy thừa cùng cơ số Lời giải chi tiết :
Ta có \({\left( { - 3x} \right)^5}:{\left( { - 3x} \right)^2} \)\(= {\left( { - 3x} \right)^3} \)\(= {\left( { - 3} \right)^3}.{x^3} = - 27{x^3}\). Chú ý
Một số em có thể nhầm dấu \({\left( { - 3} \right)^3} = 27\) dẫn đến chọn sai đáp án.
Câu 7 :
Thương của phép chia \(\left( {9{x^4}{y^3} - 18{x^5}{y^4} - 81{x^6}{y^5}} \right):\left( { - 9{x^3}{y^3}} \right)\) là đa thức có bậc là:
Đáp án : A Phương pháp giải :
+ Sử dụng quy tắc chia đa thức cho đơn thức. + Xác định bậc của đa thức là bậc cao nhất của các đơn thức trong đa thức. Lời giải chi tiết :
Ta có \(\left( {9{x^4}{y^3} - 18{x^5}{y^4} - 81{x^6}{y^5}} \right):\left( { - 9{x^3}{y^3}} \right)\)\( = \left[ {\left( {9{x^4}{y^3}} \right):\left( { - 9{x^3}{y^3}} \right)} \right] - \left[ {18{x^5}{y^4}:\left( { - 9{x^3}{y^3}} \right)} \right] - \left[ {81{x^6}{y^5}:\left( { - 9{x^3}{y^3}} \right)} \right]\) \( = - x + 2{x^2}y + 9{x^3}{y^2}\) Đa thức \( - x + 2{x^2}y + 9{x^3}{y^2}\) có bậc \(3 + 2 = 5\) . Chú ý
Một số em không nhớ cách tính bậc của đa thức dẫn đến cộng tất cả số mũ của biến dẫn đến ra đáp án B sai.
Câu 8 :
Biết phần dư của phép chia đa thức \(\left( {{x^5} + {x^3} + {x^2} + 2} \right)\) cho đa thức \(\left( {{x^3} + 1} \right)\) là số tự nhiên \(a\) . Chọn câu đúng.
Đáp án : A Lời giải chi tiết :
 Phần dư của phép chia là \(a = 1 < 2\) Chú ý
Một số em sai ở phép trừ cuối \(\left( {{x^3} + 2} \right) - \left( {{x^3} + 1} \right) = {x^3} + 2 - {x^3} + 1 = 3\) do không đổi dấu khi phá ngoặc nên dẫn đến chọn sai đáp án.
Câu 9 :
Hãy chọn câu sai
Đáp án : B Phương pháp giải :
Ta sử dụng định lý đường trung bình và hình thang Lời giải chi tiết :
+ Độ dài đường trung bình hình thang bằng nửa tổng hai đáy nên đáp án B sai.
Câu 10 :
Tính độ dài đường trung bình của hình thang cân, biết rằng hai đường chéo vuông góc với nhau và đường cao của nó bằng $10cm$ .
Đáp án : D Phương pháp giải :
Ta đi chứng minh độ dài đường trung bình của hình thang cân \(ABCD\) bằng với độ dài đường cao đi qua giao điểm của hai đường chéo của hình thang. Từ đó suy ra độ dài đường trung bình của hình thang. Lời giải chi tiết :
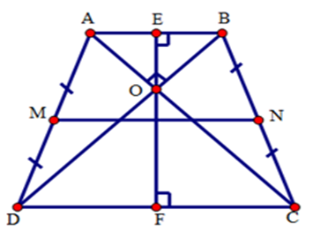 + Xét hình thang cân $ABCD\left( {AB//CD} \right)$ , hai đường chéo $AC$ và $BD$ vuông góc với nhau tại $O,{\rm{ }}MN$ là đường trung bình của hình thang $ABCD$ . Qua $O$ kẻ đường thẳng vuông góc với $AB$ tại $E$ , với $CD$ tại $F$ . Xét \(\Delta ADC\) và \(\Delta BCD\) có: \(AD = BC\) (gt) DC cạnh chung \(\widehat {ADC} = \widehat {BCD}\) (gt) \( \Rightarrow \Delta ADC = \Delta BCD(c.g.c) \Rightarrow \widehat {ACD} = \widehat {BDC}\) ( hai góc tương ứng)\( \Rightarrow \Delta OCD\) cân tại O\( \Rightarrow OC = OD\) Mà \(AC = BD\) nên \(OA = OB \Rightarrow \Delta OAB\) cân tại $O$ . Lại có \(\widehat {AOB} = 90^\circ \) ( do $AB$ vuông góc với $CD$) nên \(\Delta AOB\) vuông cân tại $O$, do đó $OE$ là đường cao cũng là đường trung tuyến nên \(OE = \dfrac{{AB}}{2}.\) Tương tự: tam giác $DOC$ vuông cân tại $O$ nên $FO = \dfrac{{CD}}{2}$ Do đó \(FE = \dfrac{{AB + CD}}{2}\) $MN$ là đường trung bình của hình thang $ABCD$ nên \(MN = \dfrac{{AB + CD}}{2}\) \( \Rightarrow MN = FE = 10cm\) .
Câu 11 :
Hãy chọn câu đúng. Tứ giác $ABCD$ là hình bình hành nếu.
Đáp án : D Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình bình hành. + Tứ giác có các cạnh đối song song là hình bình hành + Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. + Tứ giác có các góc đối bằng nhau là hình bình hành Lời giải chi tiết :
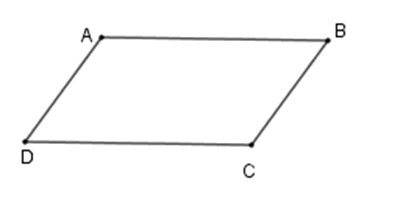 + Tứ giác \(ABCD\) là hình bình hành khi $AB$ //$CD$ ,$BC{\rm{//}}AD$ nên C sai. + Tứ giác \(ABCD\) là hình bình hành khi $\widehat A = \widehat C;\widehat B = \widehat D$ nên D đúng. + A, B sai vì chưa đủ điều kiện để kết luận. Chú ý
Một số em chọn C là sai vì ở dấu hiệu nhận biết : “Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.” Nghĩa là phải cùng một cặp cạnh đối vừa song song vừa bằng nhau thì tứ giác đó là hình bình hành.
Câu 12 :
Cho hình bình hành $ABCD$ . Gọi $I,{\rm{ }}K$ theo thứ tự là trung điểm của $CD,{\rm{ }}AB$ . Đường chéo $BD$ cắt $AI,{\rm{ }}CK$ theo thứ tự ở $E,{\rm{ }}F$ . Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Bước 1: Chứng minh tứ giác $AKCI$ là hình bình hành để suy ra \(AI{\rm{//}}CK\) .Bước 2: Sau đó sử dụng định lí đường trung bình của các tam giác \(\Delta DCF,\Delta ABE\) để suy ra mối quan hệ giữa \(DE;\,EF;\,FB\) . Lời giải chi tiết :
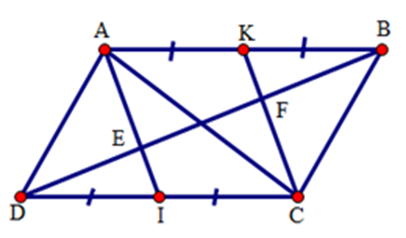 Vì \(AK = \dfrac{{AB}}{2},IC = \dfrac{{CD}}{2}\) (gt) mà \(AB = CD\) (cạnh đối hình bình hành) nên \(AK = IC\) . Vì $AB{\rm{//}}CD(gt),K \in AB,I \in DC \Rightarrow AK{\rm{//}}IC$ . Tứ giác $AKCI$ có \(AK{\rm{//}}CI,AK = IC(cmt)\) nên là hình bình hành. Suy ra \(AI{\rm{//}}CK\) . Mà \(E \in AI,F \in CK \Rightarrow EI{\rm{//}}CF,KF{\rm{//}}AE\) . Xét \(\Delta DCF\) có: \(DI = IC(gt),IE{\rm{//}}CF(cmt) \Rightarrow ED = FE\,\,\,(1)\) Xét \(\Delta ABE\) có: \(AK = KB(gt),KF{\rm{//}}AE(cmt) \Rightarrow EF = FB\,\,\,\,(2)\). Từ (1) và (2) suy ra \(ED = FE = FB\).
Câu 13 :
Cho tứ giác \(ABCD\), lấy \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA.\) Tứ giác \(ABCD\) cần có điều kiện gì để \(MNPQ\) là hình chữ nhật.
Đáp án : D Phương pháp giải :
Bước 1: Chứng minh \(MNPQ\) là hình bình hành bằng cách chứng minh cặp cạnh song song và bằng nhau được suy ra từ tính chất đường trung bình. Bước 2: Dựa vào dấu hiệu nhận biết “hình bình hành có một góc vuông là hình chữ nhật” suy ra điều kiện của \(ABCD\) để hình bình hành \(MNPQ\) là hình chữ nhật. Lời giải chi tiết :
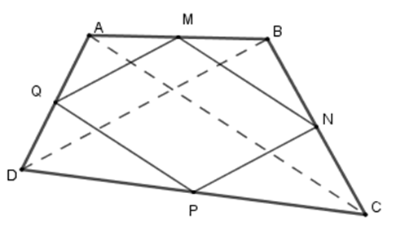 Nối \(AC\) , $BD$. + Xét tam giác \(ABD\) có \(M,\,Q\) lần lượt là trung điểm của \(AB;\,AD\) nên \(MQ\) là đường trung bình của tam giác \(ABD\) Suy ra \(MQ{\rm{//}}BD;\,MQ = \dfrac{1}{2}BD\) \(\left( 1 \right)\) . + Tương tự, xét tam giác \(CBD\) có \(N,P\) lần lượt là trung điểm của \(BC;\,CD\) nên \(NP\) là đường trung bình của tam giác \(CBD\). Suy ra \(NP{\rm{//}}BD;\,NP = \dfrac{1}{2}BD\)\(\left( 2 \right)\) Từ \(\left( 1 \right);\,\left( 2 \right) \Rightarrow MQ{\rm{//}}NP;\,MQ = NP \Rightarrow MNPQ\) là hình bình hành (dấu hiệu nhận biết). + Để hình bình hành \(MNPQ\) là hình chữ nhật thì \(\widehat {MQP} = 90^\circ \) hay \(MQ \bot QP\) Lại có \(QP{\rm{//}}AC\) (do \(QP\) là đường trung bình của tam giác \(DAC\) ) nên \(MQ \bot AC\) mà \(MQ{\rm{//}}BD\) (cmt) nên \(AC \bot BD\) . Vậy tứ giác \(ABCD\) cần có \(AC \bot BD\) thì \(MNPQ\) là hình chữ nhật.
Câu 14 :
Cho tam giác $ABC,$ đường cao $AH$ . Gọi $I$ là trung điểm của $AC,E$ là điểm đối xứng với $H$ qua $I$. Tứ giác $AECH$ là hình gì?
Đáp án : A Phương pháp giải :
+ Chứng minh $AECH$ là hình bình hành dựa vào dấu hiệu tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành. + Chứng minh hình bình hành $AECH$ là hình chữ nhật dựa vào dấu hiệu hình bình hành có một góc vuông là hình chữ nhật. Lời giải chi tiết :
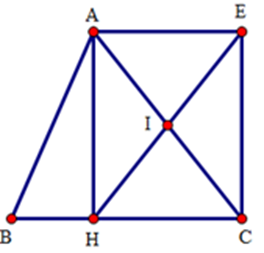 Xét tứ giác $AECH$ có: $I$ là trung điểm của $AC$ (gt); $I$ là trung điểm của $HE$ (do $H$ và $E$ đối xứng nhau qua $I$ ) Do đó $AECH$ là hình bình hành (dấu hiệu nhận biết). Lại có \(\widehat {AHC} = {90^ \circ }\) , nên $AECH$ là hình chữ nhật (dhnb).
Câu 15 :
Cho hình chữ nhật $ABCD$ có \(AB = a;\,AD = b\) . Cho $M$ , $N$ , $P$ , $Q$ là các đỉnh của tứ giác $MNPQ$ và lần lượt thuộc các cạnh $AB$ , $BC$ ,$CD,DA$ . Tìm giá trị nhỏ nhất của chu vi tứ giác $MNPQ$ .
Đáp án : C Phương pháp giải :
Bước 1: Gọi thêm các điểm $I,H,K$ lần lượt là trung điểm của các đoạn thẳng $QM,QN,PN$ . Bước 2: Ta tính chu vi tứ giác $MNPQ$ : \( AI = \dfrac{1}{2}QM, \)\(IH= \dfrac{1}{2}MN,\)\(HK = \dfrac{1}{2}PQ,\)\(KC= \dfrac{1}{2}NP\)\( \Rightarrow AI + IH + HK + KC \)\(= \dfrac{1}{2}(QM + MN + PQ + NP) \)\(= \dfrac{1}{2}{P_{MNPQ}}\) Mà \(AI + IH + HK + KC \ge AC\), từ đó suy ra lời giải bài toán. Bước 3: Dùng định lý Pytago tính \(AC\) theo $a,\,b$ rồi kết luận. Lời giải chi tiết :
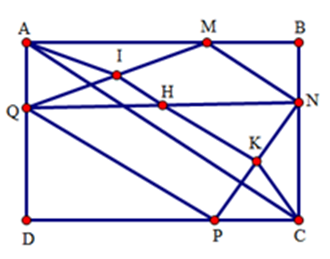 Gọi $I,H,K$ lần lượt là trung điểm các đoạn $QM,QN,PN$ . Xét tam giác $AQM$ vuông tại $A$ có $AI$ là đường trung tuyến nên suy ra \(AI = \dfrac{1}{2}QM\). $IH$ là đường trung bình của tam giác $QMN$ nên \(IH = \dfrac{1}{2}MN\), $IH$ //$MN$ . Tương tự \(KC = \dfrac{1}{2}NP,HK = \dfrac{1}{2}PQ\), $HK$ //$PQ$ . Do đó $AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} = \dfrac{1}{2}{P_{MNPQ}}$ Mặt khác nếu xét các điểm $A,I,H,K,C$ ta có: $AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} \ge AC$ Do đó \({P_{MNPQ}} \ge 2AC\) (không đổi) Dấu “=” xảy ra khi và chỉ khi $A,I,H,K,C$ thẳng hàng theo thứ tự đó. Điều đó tương đương với $MN$ //$AC$ //$QP$ , $QM$ //$BD$ //$NP$ hay $MNPQ$ là hình bình hành. Theo định lý Pytago cho tam giác \(ACB\) vuông tại \(A\) ta có \(A{C^2} = A{B^2} + B{C^2} = A{B^2} + A{D^2}\) \( = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \) . Vậy giá trị nhỏ nhất của chu vi $MNPQ$ là $2AC$ \( = 2\sqrt {{a^2} + {b^2}} \) .
Câu 16 :
Hình thoi không có tính chất nào dưới đây?
Đáp án : C Lời giải chi tiết :
Hình thoi có tất cả các tính chất của hình bình hành + Các cạnh đối song song và bằng nhau, các góc đối bằng nhau + Hai đường chéo giao nhau tại trung điểm mỗi đường. Ngoài ra còn có + Hai đường chéo vuông góc với nhau. + Hai đường chéo là các đường phân giác của các góc của hình thoi.
Câu 17 :
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
Đáp án : A Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình thoi Lời giải chi tiết :
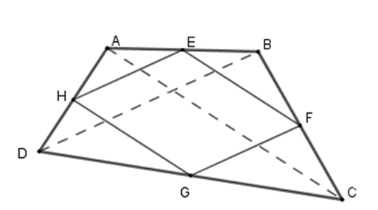 Vì $E,F$ lần lượt là trung điểm của$AB$ , $BC$ nên $EF$ là đường trung bình của $\Delta ABC$ . Suy ra \(EF{\rm{//}}AC\) và \(EF = \dfrac{1}{2}AC\) (1). Tương tự ta có : \(HG{\rm{//}}AC\) và \(HG = \dfrac{1}{2}AC\) (2). Từ (1) và (2) suy ra tứ giác $EFGH$ là hình bình hành. Muốn cho tứ giác $EFGH$ là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau. Nên \(EH = EF \Leftrightarrow AC = BD\).
Câu 18 :
Cho hình vuông $ABCD$ . Trên các cạnh $AB,BC,CD,DA$ lần lượt lấy các điểm $E,F,G,H$ sao cho $AE = BF = CG = DH$ . Tứ giác \(EFGH\) là hình gì?
Đáp án : D Phương pháp giải :
Bước 1: Ta chứng minh \(DG = CF = EB = AH\). Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) nên \(HG = GF = HE = EF\) . Do đó tứ giác \(EFGH\) là hình thoi. Bước 2: Chứng minh góc \(\widehat {HEF} = 90^\circ \) để suy ra \(EFGH\) là hình vuông. Lời giải chi tiết :
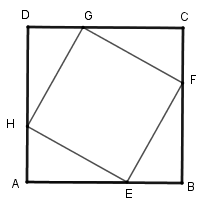 + Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\) (tính chất). Mà $AE = BF = CG = DH\,\left( {gt} \right)$ nên \(AB - AE = BC - BF = CD - CG = DA - DH\) hay \(DG = CF = EB = AH\). Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) (c-g-c) nên \(HG = GF = HE = EF\). Vì \(HG = GF = HE = EF\) nên tứ giác \(EFGH\) là hình thoi. + Vì \(\Delta AHE = \Delta BEF\,\left( {cmt} \right) \Rightarrow \widehat {AHE} = \widehat {BEF}\) (hai góc tương ứng) mà \(\widehat {AHE} + \widehat {HEA} = 90^\circ \Rightarrow \widehat {BEF} + \widehat {HEA} = 90^\circ \) Từ đó \(\widehat {HEF} = 180^\circ - \left( {\widehat {HEA} + \widehat {BEF}} \right) = 180^\circ - 90^\circ = 90^\circ \) . Hình thoi \(EFGH\) có \(\widehat {HEF} = 90^\circ \) nên \(EFGH\) là hình vuông.
Câu 19 :
Cho hình vuông có chu vi \(28\,cm\) . Độ dài cạnh hình vuông là:
Đáp án : B Lời giải chi tiết :
Hình vuông có bốn cạnh bằng nhau nên chu vi hình vuông bằng \(4a\) . (\(a\) là độ dài một cạnh) Từ giả thiết ta có \(4a = 28 \Leftrightarrow a = 7\,cm\) . Vậy cạnh hình vuông là \(a = 7\,cm\) .
Câu 20 :
Cho $B = {\left( {{x^2} + 3} \right)^2} - {x^2}\left( {{x^2} + 3} \right) - 3\left( {x + 1} \right)\left( {x - 1} \right)$. Chọn câu đúng.
Đáp án : D Phương pháp giải :
Sử dụng công thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) , \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\) và phép nhân đa thức để khai triển và rút gọn. Lời giải chi tiết :
Ta có $B = {\left( {{x^2} + 3} \right)^2} - {x^2}\left( {{x^2} + 3} \right) - 3\left( {x + 1} \right)\left( {x - 1} \right)$\( = {\left( {{x^2}} \right)^2} + 2.{x^2}.3 + {3^2} - \left( {{x^2}.{x^2} + {x^2}.3} \right) - 3\left( {{x^2} - 1} \right)\) \( = {x^4} + 6{x^2} + 9 - {x^4} - 3{x^2} - 3{x^2} + 3\) \( = 12\) . Chú ý
Một số em có thể nhầm dấu ở phép biến đổi \( - 3\left( {{x^2} - 1} \right) = - 3{x^2} - 3\) dẫn đến \(B = 6\) , chọn A sai.
Câu 21 :
Tìm giá trị \(x\) thỏa mãn \(2x\left( {x - 3} \right) - \left( {3 - x} \right) = 0\)
Đáp án : A Phương pháp giải :
+ Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử + Từ đó đưa về dạng \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) Lời giải chi tiết :
Ta có \(2x\left( {x - 3} \right) - \left( {3 - x} \right) = 0\)\( \Leftrightarrow 2x\left( {x - 3} \right) + \left( {x - 3} \right) = 0 \Leftrightarrow \left( {x - 3} \right)\left( {2x + 1} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\2x + 1 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\2x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - \dfrac{1}{2}\end{array} \right.\) Vậy \(x = 3;\,x = - \dfrac{1}{2}\) Chú ý
Một số em có thể sai dấu ở bước phân tích \( - \left( {3 - x} \right) = - \left( {x - 3} \right)\) dẫn đến ra sai đáp án.
Câu 22 :
Thu gọn biểu thức \(\dfrac{1}{9}{x^2}{y^3}:{\left( { - 3xy} \right)^2}\) ta được
Đáp án : A Phương pháp giải :
Sử dụng các công thức lũy thừa của một tích\({\left( {x.y} \right)^m} = {x^m}.{y^m}\) và thương các lũy thừa\({x^m}:{x^n} = {x^{m - n}}\,\,\left( {m \ge n,\,m,\,n \in \mathbb{N}} \right)\) Lời giải chi tiết :
Tacó\(\dfrac{1}{9}{x^2}{y^3}:{\left( { - 3xy} \right)^2} = \dfrac{1}{9}{x^2}{y^3}:\left[ {{{\left( { - 3} \right)}^2}{x^2}{y^2}} \right]\)\( = \dfrac{1}{9}{x^2}{y^3}:\left( {9{x^2}{y^2}} \right) = \dfrac{1}{{81}}y\) Chú ý
Một số em có thể quên bình phương hệ số \( - 3\) dẫn đến chọn phương án B sai. Hoặc nhầm dấu khi bình phương \({\left( { - 3} \right)^2} = - 9\) dẫn đến chọn D sai.
Câu 23 :
Chọn câu sai.
Đáp án : C Phương pháp giải :
Sử dụng các công thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\), \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) , \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) Lời giải chi tiết :
Ta có \({\left( {x + 2y} \right)^2} = {x^2} + 2x.2y + {\left( {2y} \right)^2}\)\( = {x^2} + 4xy + 4{y^2}\) nên A đúng \({\left( {x - 2y} \right)^2} = {x^2} - 2x.2y + {\left( {2y} \right)^2}\)\( = {x^2} - 4xy + 4{y^2}\) nên B đúng, C sai. \(\left( {x - 2y} \right)\left( {x + 2y} \right) = {x^2} - {\left( {2y} \right)^2} = {x^2} - 4{y^2}\) nên D đúng.
Câu 24 :
So sánh \(A = 2019.2021.a\) và \(B = \left( {{{2019}^2} + 2.2019 + 1} \right).a\) (với \(a > 0\))
Đáp án : D Phương pháp giải :
Biến đổi \(A\) để sử dụng công thức \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\) , \({A^2} + 2AB + {B^2} = {\left( {A + B} \right)^2}\) Sau đó so sánh \(A\) và \(B\) . Lời giải chi tiết :
Ta có \(A = 2019.2021.a\)\( = \left( {2020 - 1} \right)\left( {2020 + 1} \right)a = \left( {{{2020}^2} - 1} \right)a\) Và \(B = \left( {{{2019}^2} + 2.2019 + 1} \right)a = {\left( {2019 + 1} \right)^2}a = {2020^2}a\) Vì \({2020^2} - 1 < {2020^2}\) và \(a > 0\) nên \(\left( {{{2020}^2} - 1} \right)a < {2020^2}a\) hay \(A < B\) . Chú ý
Một số em có thể nhầm hằng đẳng thức \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + {B^2}\) dẫn đến \(A > B\) nên chọn C sai.
Câu 25 :
Viết biểu thức \(\left( {\dfrac{y}{2} + 6} \right)\left( {\dfrac{{{y^2}}}{4} - 3y + 36} \right)\) dưới dạng tổng hai lập phương
Đáp án : B Phương pháp giải :
Sử dụng công thức hiệu hai lập phương \(\left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right) = {A^3} + {B^3}\) Lời giải chi tiết :
Ta có \(\left( {\dfrac{y}{2} + 6} \right)\left( {\dfrac{{{y^2}}}{4} - 3y + 36} \right)\)\( = \left( {\dfrac{y}{2} + 6} \right)\left( {{{\left( {\dfrac{y}{2}} \right)}^2} - \dfrac{y}{2}.6 + {6^2}} \right)\)\( = {\left( {\dfrac{y}{2}} \right)^3} + {6^3}\)
Câu 26 :
Cho \({\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)\). Khi đó
Đáp án : D Phương pháp giải :
Biến đổi giả thiết bằng cách sử dụng hằng đẳng thức \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)\) \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\) Từ đó đưa về dạng \({A^2} + {B^2} + {C^2} = 0 \Leftrightarrow A = B = C = 0\) Lời giải chi tiết :
Ta có \({\left( {a + b + c} \right)^2} + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + bc + ca} \right)\) \( \Leftrightarrow {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right) + 12 = 4\left( {a + b + c} \right) + 2\left( {ab + ac + bc} \right)\) \( \Leftrightarrow {a^2} + {b^2} + {c^2} - 4a - 4b - 4c + 12 = 0\) \( \Leftrightarrow \left( {{a^2} - 4a + 4} \right) + \left( {{b^2} - 4b + 4} \right) + \left( {{c^2} - 4c + 4} \right) = 0\) \( \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} = 0\) Mà \({\left( {a - 2} \right)^2} \ge 0;\,{\left( {b - 2} \right)^2} \ge 0;{\left( {c - 2} \right)^2} \ge 0\) với mọi \(a,b,c.\) Nên \({\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} \ge 0\) với mọi \(a,b,c\) Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}a - 2 = 0\\b - 2 = 0\\c - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 2\\c = 2\end{array} \right. \Leftrightarrow a = b = c = 2\)
Câu 27 :
Cho \(27{x^3} - 0,001 = \left( {3x - 0,1} \right)\left( {...} \right)\) . Biểu thức thích hợp điền vào dấu \(...\) là
Đáp án : C Phương pháp giải :
Sử dụng hằng đẳng thức \({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\) để phân tích đa thức thành nhân tử. Lời giải chi tiết :
Ta có \(27{x^3} - 0,001 = {\left( {3x} \right)^3} - {\left( {0,1} \right)^3} = \left( {3x - 0,1} \right)\left( {{{\left( {3x} \right)}^2} + 3x.0,1 + 0,{1^2}} \right)\)\( = \left( {3x - 0,1} \right)\left( {9{x^2} + 0,3x + 0,01} \right)\) Chú ý
Một số em có thể nhầm khi bình phương \(27{x^3} = {\left( {9x} \right)^3}\) dẫn đến chọn sai đáp án. Hoặc nhầm hằng đẳng thức \({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} - AB + {B^2}} \right)\)
Câu 28 :
Cho \({x^6} - 1 = \left( {x + A} \right)\left( {x + B} \right)\left( {{x^4} + {x^2} + C} \right)\), biết \(A,\,B,C\) là các số nguyên. Khi đó \(A + B + C\) bằng
Đáp án : B Phương pháp giải :
Sau đó sử dụng hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right);\,{A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\) để biến đổi. Lời giải chi tiết :
Ta có \({x^6} - 1 = {\left( {{x^2}} \right)^3} - 1 \)\(= \left( {{x^2} - 1} \right)\left( {{x^4} + {x^2} + 1} \right)\)\( = \left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^4} + {x^2} + 1} \right)\) \( \Rightarrow A = - 1;B = C = 1\) Suy ra \(A + B + C = - 1 + 1 + 1 = 1\) .
Câu 29 :
Cho \({x^2} - 4xy + 4{y^2} - 4 = \left( {x - my + 2} \right)\left( {x - 2y - 2} \right)\) với \(m \in \mathbb{R}\) . Chọn câu đúng
Đáp án : B Phương pháp giải :
Sử dụng phương pháp nhóm hạng tử thích hợp để phân tích đa thức thành nhân tử. Nhóm ba hạng tử đầu và sử dụng các hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2};\,{A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) Lời giải chi tiết :
Ta có \({x^2} - 4xy + 4{y^2} - 4 = \left( {{x^2} - 2.x.2y + {{\left( {2y} \right)}^2}} \right) - 4\)\( = {\left( {x - 2y} \right)^2} - {2^2} = \left( {x - 2y - 2} \right)\left( {x - 2y + 2} \right)\) Suy ra \(m = 2\) . Chú ý
Một số em có thể nhầm dấu dẫn đến \(m = - 2\) nên chọn sai đáp án.
Câu 30 :
Tính giá trị của biểu thức \(B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\) khi \({x^3} - x = 6\)
Đáp án : B Phương pháp giải :
Sử dụng phương pháp giao hoán, kết hợp và tách hạng tử (tách hạng tử thứ 2 thành 2 hạng tử giống nhau) để sắp xếp và tạo ra các hạng tử cần thiết. Sau khi tách hạng tử, nhóm hạng tử thứ 1 với hạng tử thứ 2, nhóm hạng tử thứ 3 với hạng tử thứ 5và nhóm hạng tử thứ 4 với hạng tử thứ 6 để xuất hiện nhân tử chung giống với \({x^3} - x\). Đặt nhân tử chung để được tích của các đa thức. Sau đó thế biểu thức \({x^3} - x = 6\) vào biểu thức vừa biến đổi để tính giá trị biểu thức. Lời giải chi tiết :
\(\begin{array}{l}\,\,\,\,\,\,\,\,B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = {x^6} - {x^4} - {x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = \left( {{x^6} - {x^4}} \right) - \left( {{x^4} - {x^2}} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = {x^3}\left( {{x^3} - x} \right) - x\left( {{x^3} - x} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = \left( {{x^3} - x + 1} \right)\left( {{x^3} - x} \right)\end{array}\) Tại \({x^3} - x = 6\), ta có: \(B = \left( {6 + 1} \right).6 = 7.6 = 42\)
Câu 31 :
Phân tích đa thức \(A = ab\left( {a + b} \right) - bc\left( {b + c} \right) - ac\left( {c - a} \right)\) thành nhân tử ta được
Đáp án : B Phương pháp giải :
- Ta viết \(b + c = \left( {a + b} \right) + \left( {c - a} \right)\) từ đó nhóm các hạng tử thích hợp Lời giải chi tiết :
Ta có \(b + c = \left( {a + b} \right) + \left( {c - a} \right)\) nên \(A = ab\left( {a + b} \right) - bc\left[ {\left( {a + b} \right) + \left( {c - a} \right)} \right] - ac\left( {c - a} \right)\) \( = ab\left( {a + b} \right) - bc\left( {a + b} \right) - bc\left( {c - a} \right) - ac\left( {c - a} \right)\) \( = b\left( {a + b} \right)\left( {a - c} \right) - c\left( {c - a} \right)\left( {b + a} \right)\) \( = \left( {a + b} \right)\left( {a - c} \right)\left( {b + c} \right)\)
Câu 32 :
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
Đáp án : A Phương pháp giải :
+ Sử dụng cách chia đa thức một biến đã sắp xếp. + Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết. Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) . Lời giải chi tiết :
Ta có 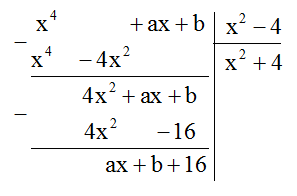 Để \({x^4} + ax + b\) chia hết cho \({x^2} - 4\) thì \(ax + b + 16 = 0 \Leftrightarrow \left\{ \begin{array}{l}ax = 0\\b + 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = - 16\end{array} \right.\) |


















