Đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 trường THCS Nguyễn Tri PhươngGiải chi tiết đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 trường THCS Nguyễn Tri Phương với cách giải nhanh và chú ý quan trọng Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1 (2,5 điểm): Giải phương trình: a) \(5\left( {x - 3} \right) + 3\left( {x + 5} \right) = 7x - 13\) b) \(\dfrac{{2x - 4}}{{x - 3}} + \dfrac{6}{{3x - {x^2}}} = \dfrac{{x - 1}}{x}\) c) \(\left( {x - 2} \right)\left( {2x - 5} \right) = {x^2} - 2x\) Bài 2 (1,5 điểm): Giải bất phương trình và biểu diễn tập nghiệm trên trục số: a) \(4\left( {x + 2} \right) - 1 > 2\left( {x + 3} \right)\) b) \(\dfrac{{7\left( {2 - x} \right)}}{6} - 2 \ge \dfrac{{2\left( {x - 1} \right)}}{3}\) Bài 3 (2 điểm): Giải bài toán bằng cách lập phương trình: Một người công nhân phải sản xuất một số khẩu trang trong một thời gian nhất định. Theo kế hoạch mỗi ngày người công nhân đó phải hoàn thành 80 chiếc khẩu trang. Vì dịch COVID-19 xáy ra nên số lượng khẩu trang khan hiếm do đó công ty yêu cầu cải tiến kĩ thuật nên mỗi ngày người công nhân đó làm được nhiều hơn kế hoạch là 10 chiếc khẩu trang. Vì vậy, chẳng những hoàn thành kế hoạch sớm hơn dự định 2 ngày mà còn vượt mức 10 chiếc khẩu trang. Hỏi theo kế hoạch người công nhân đó phải làm bao nhiêu chiếc khẩu trang? Bài 4 (3,5 điểm): Cho tam giác nhọn ABC \(\left( {AB < AC} \right)\), hai đường cao BD và CE \(\left( {E \in AB,D \in AC} \right)\) a) Chứng minh \(\Delta ABD\) đồng dạng \(\Delta ACE\) b) Chứng minh \(\Delta ABC\) đồng dạng với \(\Delta ADE\), từ đó suy ra: \(AD.BC = AB.DE\) c) Gọi giao điểm của BD và CE là H. Chứng minh \(BH.BD + CH.CE = B{C^2}\) Bài 5 (0,5 điểm): Cho \(a,b,c > 0\) thỏa mãn \(a + b + c = 1\) Tìm giá trị lớn nhất của biểu thức: \(P = \dfrac{a}{{a + 1}} + \dfrac{b}{{b + 1}} + \dfrac{c}{{c + 1}}\) HẾT LG bài 1 Phương pháp giải: a) Nhân phá ngoặc rồi chuyển vế đưa về dạng \(ax + b = 0\left( {a \ne 0} \right)\) \( \Leftrightarrow x = - \dfrac{b}{a}\) b) Tìm điều kiện Quy đồng mẫu các phân thức Khử mẫu rồi giải phương trình thu được So sánh với điều kiện và kết luận nghiệm c) Nhân phá ngoặc rồi chuyển vế. Biến đổi đưa phương trình về dạng \(A\left( x \right).B\left( x \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) Lời giải chi tiết: a) \(5\left( {x - 3} \right) + 3\left( {x + 5} \right) = 7x - 13\) \(\begin{array}{l} \Leftrightarrow 5x - 15 + 3x + 15 = 7x - 13\\ \Leftrightarrow 8x = 7x - 13\\ \Leftrightarrow 8x - 7x = - 13\\ \Leftrightarrow x = - 13\end{array}\) Vậy tập nghiệm của phương trình \(S = \left\{ { - 13} \right\}\) b) \(\dfrac{{2x - 4}}{{x - 3}} + \dfrac{6}{{3x - {x^2}}} = \dfrac{{x - 1}}{x}\) Điều kiện: \(x \ne 0;x \ne 3\) \(\dfrac{{2x - 4}}{{x - 3}} + \dfrac{6}{{3x - {x^2}}} = \dfrac{{x - 1}}{x}\) \( \Leftrightarrow \dfrac{{2x - 4}}{{x - 3}} - \dfrac{6}{{{x^2} - 3x}} = \dfrac{{x - 1}}{x}\) \( \Leftrightarrow \dfrac{{\left( {2x - 4} \right).x}}{{x\left( {x - 3} \right)}} - \dfrac{6}{{x\left( {x - 3} \right)}}\) \( = \dfrac{{\left( {x - 1} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}}\) \( \Leftrightarrow \dfrac{{2{x^2} - 4x - 6}}{{x\left( {x - 3} \right)}} = \dfrac{{{x^2} - 4x + 3}}{{x\left( {x - 3} \right)}}\) \( \Rightarrow 2{x^2} - 4x - 6 = {x^2} - 4x + 3\) \( \Leftrightarrow 2{x^2} - {x^2} - 4x + 4x\)\( = 6 + 3\) \(\begin{array}{l} \Leftrightarrow {x^2} = 9\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\end{array}\) Vậy phương trình có tập nghiệm \(S = \left\{ { - 3;3} \right\}\) c) \(\left( {x - 2} \right)\left( {2x - 5} \right) = {x^2} - 2x\) \( \Rightarrow 2{x^2} - 5x - 4x + 10 = {x^2} - 2x\) \( \Leftrightarrow 2{x^2} - 5x - 4x + 10 - {x^2} + 2x = 0\) \( \Leftrightarrow {x^2} - 7x + 10 = 0\) \(\begin{array}{l} \Leftrightarrow {x^2} - 2x - 5x + 10 = 0\\ \Leftrightarrow x\left( {x - 2} \right) - 5\left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 5 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 5\end{array} \right.\end{array}\) Vậy phương trình có tập nghiệm \(S = \left\{ {2;5} \right\}\) LG bài 2 Phương pháp giải: a) Chuyển vế đưa về giải bất phương trình bậc nhất 1 ẩn \(ax + b > 0\) b) Quy đồng mẫu số, bỏ mẫu rồi đưa về giải bất phương trình bậc nhất một ẩn. Lời giải chi tiết: a) \(4\left( {x + 2} \right) - 1 > 2\left( {x + 3} \right)\) \(\begin{array}{l} \Leftrightarrow 4x + 8 - 1 > 2x + 6\\ \Leftrightarrow 4x + 7 > 2x + 6\\ \Leftrightarrow 4x - 2x > 6 - 7\\ \Leftrightarrow 2x > - 1\\ \Leftrightarrow x > \dfrac{{ - 1}}{2}\end{array}\) Vậy bất phương trình có tập nghiệm \(S = \left\{ {x|x > - \dfrac{1}{2}} \right\}\) Biểu diễn tập nghiệm trên trục số: b) \(\dfrac{{7\left( {2 - x} \right)}}{6} - 2 \ge \dfrac{{2\left( {x - 1} \right)}}{3}\) \( \Leftrightarrow \dfrac{{7\left( {2 - x} \right)}}{{6}} - \dfrac{{12}}{{6}} \ge \dfrac{{2.2\left( {x - 1} \right)}}{{6}}\) \(\begin{array}{l} \Leftrightarrow \dfrac{{7\left( {2 - x} \right) - 12}}{{6}} \ge \dfrac{{4\left( {x - 1} \right)}}{{6}}\\ \Leftrightarrow 7\left( {2 - x} \right) - 12\ge 4\left( {x - 1} \right)\\ \Leftrightarrow 14 - 7x - 12 \ge 4x - 4\\ \Leftrightarrow 2 - 7x \ge 4x - 4\\ \Leftrightarrow - 7x - 4x \ge - 4 - 2\\ \Leftrightarrow - 11x \ge - 6\\ \Leftrightarrow x \le \dfrac{6}{11}\end{array}\) Vậy bất phương trình có tập nghiệm \(S = \left\{ {x|x \le \dfrac{6}{11}} \right\}\) Biểu diễn tập nghiệm trên trục số: LG bài 3 Phương pháp giải: Giải bài toán bằng cách lập phương trình Chọn ẩn và đặt điều kiện cho ẩn Lập phương trình và giải phương trình So sánh với điều kiện và kết luận nghiệm Lời giải chi tiết: Giải bài toán bằng cách lập phương trình: Một người công nhân phải sản xuất một số khẩu trang trong một thời gian nhất định. Theo kế hoạch mỗi ngày người công nhân đó phải hoàn thành 80 chiếc khẩu trang. Vì dịch COVID-19 xáy ra nên số lượng khẩu trang khan hiếm do đó công ty yêu cầu cải tiến kĩ thuật nên mỗi ngày người công nhân đó làm được nhiều hơn kế hoạch là 10 chiếc khẩu trang. Vì vậy, chẳng những hoàn thành kế hoạch sớm hơn dự định 2 ngày mà còn vượt mức 10 chiếc khẩu trang. Hỏi theo kế hoạch người công nhân đó phải làm bao nhiêu chiếc khẩu trang? Gọi số khẩu trang người đó phải làm theo kế hoạch là \(x\) (chiếc) \(\left( {x \in {\mathbb{N}^*}} \right)\) Thời gian theo kế hoạch của công nhân đó là \(\dfrac{x}{{80}}\) ngày Theo thực tế, mỗi ngày người đó làm hơn kế hoạch là 10 chiếc nên mỗi ngày người đó làm được \(80 + 10 = 90\) chiếc khẩu trang Vì tổng số khẩu trang theo thực tế vượt so với kế hoạch 10 chiếc nên số khẩu trang theo thực tế người đó làm được là: \(x + 10\) chiếc Thời gian làm theo thực tế là \(\dfrac{{x + 10}}{{90}}\) ngày Vì người đó hoàn thành kế hoạch sớm hơn 2 ngày nên ta có phương trình: \(\dfrac{x}{{80}} - \dfrac{{x + 10}}{{90}} = 2\) \(\begin{array}{l} \Leftrightarrow \dfrac{{9x - 8\left( {x + 10} \right)}}{{720}} = 2\\ \Leftrightarrow 9x - 8\left( {x + 10} \right) = 720.2\\ \Leftrightarrow 9x - 8x - 80 = 1440\\ \Leftrightarrow x - 80 = 1440\\ \Leftrightarrow x = 1440 + 80\end{array}\) \( \Leftrightarrow x = 1520\) (thỏa mãn) Vậy số khẩu trang người đó phải làm theo kế hoạch là 1520 chiếc. LG bài 4 Phương pháp giải: a) Chứng minh hai tam giác đồng dạng theo trường hợp góc – góc b) Sử dụng các trường hợp đồng dạng góc – góc và góc –cạnh –góc sau đó suy ra tỉ lệ cạnh tương ứng c) Chứng minh các cặp tam giác đồng dạng theo trường hợp góc – góc sau đó suy ra tỉ lệ cạnh tương ứng Lời giải chi tiết: Cho tam giác nhọn ABC \(\left( {AB < AC} \right)\), hai đường cao BD và CE \(\left( {E \in AB,D \in AC} \right)\)
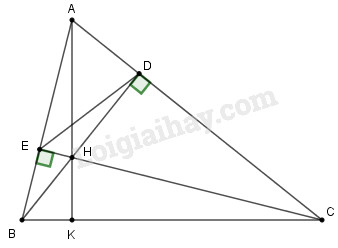
a) Chứng minh \(\Delta ABD\) đồng dạng \(\Delta ACE\) Xét tam giác \(ABD\) và tam giác \(ACE\) có: \(\widehat {AEC} = \widehat {ADB} = {90^0}\) (do \(CE \bot AC\) và \(BD \bot AC\)) \(\widehat A\) chung Suy ra \(\Delta ABD \backsim \Delta ACE\left( {g - g} \right)\) b) Chứng minh \(\Delta ABC\) đồng dạng với \(\Delta ADE\), từ đó suy ra: \(AD.BC = AB.DE\) Vì \(\Delta ABD \backsim \Delta ACE\) (câu a) nên \(\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AE}}\) Xét \(\Delta ABC\) và \(\Delta ADE\) có: \(\widehat A\) chung \(\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AE}}\) (cmt) Nên \(\Delta ABC \backsim \Delta ADE\left( {c - g - c} \right)\) \(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AD}} = \dfrac{{BC}}{{DE}}\\ \Leftrightarrow AB.DE = AD.BC\end{array}\) c) Gọi giao điểm của BD và CE là H. Chứng minh \(BH.BD + CH.CE = B{C^2}\) Kéo dài \(AH\) cắt BC tại K Vì H là giao điểm 2 đường cao của tam giác ABC nên H là trực tâm tam giác ABC Suy ra \(AH \bot BC\) tại K. Xét \(\Delta ABK\) và \(\Delta CBE\) có: \(\widehat B\) chung \(\widehat {AKB} = \widehat {BEC} = {90^0}\) Suy ra \(\Delta ABK \backsim \Delta CBE\left( {g - g} \right)\) \( \Rightarrow \dfrac{{AB}}{{BC}} = \dfrac{{BK}}{{BE}}\) \( \Leftrightarrow AB.BE = BK.BC\) (1) Xét \(\Delta AKC\) và \(\Delta BDC\) có: \(\widehat C\) chung \(\widehat {BDC} = \widehat {AKC} = {90^0}\) Suy ra \(\Delta AKC \backsim \Delta BDC\left( {g - g} \right)\) \( \Rightarrow \dfrac{{AC}}{{BC}} = \dfrac{{KC}}{{CD}}\) \( \Leftrightarrow AC.CD = BC.KC\) (2) Xét \(\Delta BEH\) và \(\Delta BDA\) có: \(\widehat {ABD}\) chung \(\widehat {BEH} = \widehat {BDA} = {90^0}\) Suy ra \(\Delta BEH \backsim \Delta BDA\left( {g - g} \right)\) \( \Rightarrow \dfrac{{BE}}{{BD}} = \dfrac{{BH}}{{BA}}\) \( \Leftrightarrow BE.BA = BH.BD\) (3) Xét \(\Delta CHD\) và \(\Delta CAE\) có: \(\widehat {ACE}\) chung \(\widehat {CDH} = \widehat {CEA} = {90^0}\) Suy ra \(\Delta CHD \backsim \Delta CAE\left( {g - g} \right)\) \( \Rightarrow \dfrac{{CH}}{{CA}} = \dfrac{{CD}}{{CE}}\) \( \Leftrightarrow CH.CE = CA.CD\) (4) Từ (1), (2), (3), (4) suy ra \(BH.BD + CH.CE\) \( = BA.BE + CA.CD\) \( = BK.BC + BC.CK\) \( = BC\left( {BK + CK} \right)\) \( = BC.BC = B{C^2}\) Vậy \(BH.BD + CH.CE\)\( = B{C^2}\) (đpcm) LG bài 5 Phương pháp giải: Chứng minh và sử dụng bất đẳng thức \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x > 0,y > 0\). Lời giải chi tiết: Trước hết ta chứng minh bất đẳng thức: \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) (*) với \(x > 0,y > 0\) Thật vậy, \(\begin{array}{l}\left( * \right) \Leftrightarrow \dfrac{{y + x}}{{xy}} \ge \dfrac{4}{{x + y}}\\ \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy\\ \Leftrightarrow {x^2} + 2xy + {y^2} - 4xy \ge 0\\ \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\end{array}\) \( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) (luôn đúng) Do đó \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x > 0,y > 0\) \( \Rightarrow \dfrac{1}{{x + y}} \le \dfrac{1}{4}\left( {\dfrac{1}{x} + \dfrac{1}{y}} \right)\) (**) Ta có:
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}a + b = a + c\\b + c = b + a\\c + a = c + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = c\\c = a\\a = b\end{array} \right.\) \( \Leftrightarrow a = b = c = \dfrac{1}{3}\). Vậy GTLN của \(P\) là \(\dfrac{3}{4}\) khi \(a = b = c = \dfrac{1}{3}\). HẾT Loigiaihay.com
|














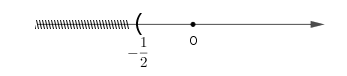
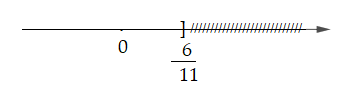
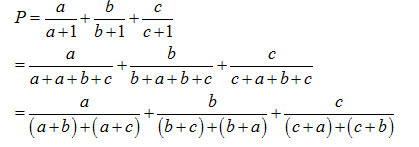







Danh sách bình luận