Giải đề thi học kì 2 toán lớp 8 năm 2020 - 2021 THCS Giảng Võ

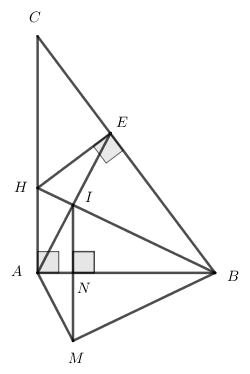
Đề bài

Bài I (2,0 điểm)

Cho biểu thức \(A = \frac{{x - 1}}{{{x^2}}}\) và \(B = \frac{1}{x} - \frac{x}{{2x + 1}} + \frac{{2{x^2} - 3x - 1}}{{2x + 1}}\) với \(x \ne 0;\,\,x \ne \frac{{ - 1}}{2};\,\,x \ne 1\)

1) Tính giá trị của biểu thức A tại x = 3;

2) Rút gọn biểu thức B;

3) Đặt C = A: B. Chứng minh: \(C \ge  - 1\).

Bài II (1,5 điểm)

1) Giải các phương trình:

a) \({\left( {x + 2} \right)^2} - 4 = 0\)

b) \(\left| x \right| = 3x + 5\)

2) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: \(2x{\rm{ }}-7 < {\rm{ }}5x{\rm{ }} + 1\).

Bài III (2,5 điểm)

1) Giải bài toán sau bằng cách lập phương trình:

Một lâm trường lập kế hoạch trồng một số ha rừng, theo đó mỗi tuần lâm trường phải trồng 15ha. Trên thực tế nhờ cải tiến kĩ thuật, lâm trường đã trồng được 20ha mỗi tuần. Do đó, lâm trường không những đã hoàn thành kế hoạch trước thời hạn 1 tuần mà còn trồng thêm được 5ha rừng. Hỏi theo kế hoạch, lâm trường phải trồng bao nhiêu ha rừng?

2) Người ta muốn lăn sơn bốn bức tường của một phòng học có dạng hình hộp chữ nhật với chiều dài 7m, chiều rộng 5m và chiều cao 3,8m. Tính diện tích các mặt tường cân sơn, biết tổng diện tích các cửa ra vào và cửa sổ của phòng học đó là 9,34m.

Bài IV (3,5 điểm) Cho tam giác ABC vuông tại A, có AB < AC. Lấy điểm H trên cạnh AC (điểm H khác điểm A và C). Gọi E là hình chiếu của điểm H trên cạnh BC.

1) Chứng minh: Tam giác ABC đồng dạng với tam giác EHC;

2) Chứng minh: \(\widehat {HBC}{\rm{ }} = {\rm{ }}\widehat {EAC};\)

3) Gọi I là giao điểm của đoạn AE và doạn BH, chứng minh: AB. HI = AI. HE;

4) Gọi M là điểm đối xứng với điểm I qua đường thẳng AB. Tìm vị trí điểm H trên cạnh AC để diện tích tứ giác MACB gấp 4 lần diện tích tứ giác IHCE.

LG câu I

Phương pháp giải:

1) Thay x= 3 vào A rồi tính giá trị của A

2) Quy đồng B rồi tính

3) Rút gọn C= A:B rồi đánh giá

Lời giải chi tiết:

1) Thay x = 3 (t/m đk) vào A ta được:

\(A = \frac{{3 - 1}}{{{3^2}}} = \frac{2}{9}\)

Vậy \(A = \frac{2}{9}\) khi \(x = 3\).

2)

\(\begin{array}{l}B = \frac{1}{x} - \frac{x}{{2x + 1}} + \frac{{2{x^2} - 3x - 1}}{{x(2x + 1)}}(x \ne 0;\,\,x \ne \frac{{ - 1}}{2};\,\,x \ne 1)\\B = \frac{{2x + 1}}{{x(2x + 1)}} - \frac{{{x^2}}}{{x(2x + 1)}} + \frac{{2{x^2} - 3x - 1}}{{x(2x + 1)}}\\B = \frac{{2x + 1 - {x^2} + 2{x^2} - 3x - 1}}{{x(2x + 1)}}\\B = \frac{{{x^2} - x}}{{x(2x + 1)}}\\B = \frac{{x(x - 1)}}{{x(2x + 1)}}\\B = \frac{{x - 1}}{{2x + 1}}\end{array}\)

3)

Ta có:

\(\begin{array}{l}C = A:B\\C = \frac{{x - 1}}{{{x^2}}}:\frac{{x - 1}}{{2x + 1}}\\C = \frac{{x - 1}}{{{x^2}}}.\frac{{2x + 1}}{{x - 1}}\\C = \frac{{2x + 1}}{{{x^2}}} = \frac{1}{{{x^2}}} + \frac{2}{x}\\C = {\left( {\frac{1}{x} + 1} \right)^2} - 1\end{array}\)

Suy ra \(C \ge  - 1\) với mọi x thỏa mãn điều kiện

LG câu II

Phương pháp giải:

1) Đưa về dạng |A|=B (B>0) \(\Leftrightarrow\) A=B hoặc A=-B

2) Chuyển vế để giải bất phương trình rồi biểu diễn tập nghiệm trên trục số.

Lời giải chi tiết:

1)

 \(\begin{array}{l}{\left( {x + 2} \right)^2} - 4 = 0\\ \Leftrightarrow {\left( {x + 2} \right)^2} = 4\\ \Leftrightarrow \left| {x + 2} \right| = 2\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 2 = 2}\\{x + 2 =  - 2}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  - 4}\end{array}} \right.\end{array}\)

Vậy phương trình có tập nghiệm: \(S = {\rm{\{ }}0;\, - 4\} \)

b)

\(\left| x \right| = 3x + 5\), đk: \(x \ge \frac{{ - 5}}{3}\)

\(\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3x + 5}\\{x =  - 3x - 5}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x =  - 5}\\{4x =  - 5}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{ - 5}}{2}(l)}\\{x = \frac{{ - 5}}{4}(t/m)}\end{array}} \right.\end{array}\)

Vậy phương trình có nghiệm \(x = \frac{{ - 5}}{4}\).

2)

\(\begin{array}{l}2x{\rm{ }}-7 < {\rm{ }}5x{\rm{ }} + 1\\ \Leftrightarrow 2x - 5x < 1 + 7\\ \Leftrightarrow  - 3x < 8\\ \Leftrightarrow x > \frac{{ - 8}}{3}\end{array}\)

Vậy bất phương trình có tập nghiệm: \(S = \left\{ {{\rm{x}}\,{\rm{|}}\,{\rm{x}}\,\,{\rm{ > }}\,\frac{{ - 8}}{3}} \right\}\)

Biểu diễn tập nghiệm trên trục số:

LG câu III

Phương pháp giải:

1) Phương pháp giải bài toán bằng cách lập hệ phương trình:

- Gọi ẩn và đặt điều kiện cho ẩn.

- Biểu diễn các đại lượng đã biết và chưa biết theo ẩn.

- Thiết lập các phương trình từ điều kiện bài cho suy ra hệ phương trình.

- Giải hệ và kết luận.

Lời giải chi tiết:

1) Gọi số ha rừng lâm trường phải trồng là x \((ha,\,\,x > 0)\)

Theo kế hoạch mỗi tuần lâm trường phải trồng 15 ha.

=> Thời gian lâm trường trồng số cây trên theo kế hoạch là: \(\frac{x}{{15}}\) (tuần)

Thực tế lâm trường đã trồng được 20 ha và trồng vượt kế hoạch 5 ha nên thời gian trồng cây thực tế là: \(\frac{{x + 5}}{{20}}\) (tuần)

Do lâm trường hoàn thành kế hoạch trược 1 tuần so với kế hoạch nên ta có phương trình:

\(\begin{array}{l}\frac{x}{{15}} - \frac{{x + 5}}{{20}} = 1\\ \Leftrightarrow \frac{{4x}}{{60}} - \frac{{3\left( {x + 5} \right)}}{{60}} = \frac{{60}}{{60}}\\ \Leftrightarrow 4x - 3x - 15 = 60\\ \Leftrightarrow x = 75\,\,(t/m)\end{array}\)

Vậy lâm trường phải trồng 75 ha.

2)

Diện tích bốn bức tường kể cả cửa là: \(2.3,8.(7 + 5) = 91,2\) (m²)

Diện tích các mặt tường cần sơn là:

\(91,2 - 9,34 = 81,86\) (m²)

LG câu IV

Phương pháp giải:

a) Chứng minh hai tam giác đồng dạng với nhau theo trường hợp góc-góc ( Chú ý hai tam giác cần chứng minh đồng dạng là tam giác vuông)

b) Dựa vào kết quả chứng minh ở câu a) để chứng minh tam giác ACE đồng dạng với tam giác BCH từ đó suy ra đpcm

c) Dựa vào tam giác HIE đồng dạng với AIB.

d) Dựa vào các cặp tam giác đồng dạng 

Lời giải chi tiết:

a) Xét tam giác ABC và tam giác EHC có:

\(\widehat {BAC} = \widehat {HEC} = {90^0}\)

\(\widehat C\) chung

\(∆ ABC \backsim ∆ EHC\) (g.g)(1)

b)

Từ (1) suy ra: \(\frac{{AC}}{{EC}} = \frac{{BC}}{{HC}}\)

Hay \(\frac{{AC}}{{BC}} = \frac{{EC}}{{HC}}\)

Xét tam giác ACE và tam giác BCH có:

\(\frac{{AC}}{{BC}} = \frac{{EC}}{{HC}}\)

\(\widehat C\) chung

Suy ra: \(\widehat {HBC} = \widehat {EAC}\) (đpcm)

c)

Ta có: \(\widehat {EHB} + \widehat {HBC} = {90^0}\)

           \(\widehat {IAB} + \widehat {EAC} = {90^0}\)

Mà \(\widehat {HBC} = \widehat {EAC}\)

Nên: \(\widehat {EHB} = \widehat {IAB}\)

Xét tam giác HIE và tam giác AIB có:

\(\widehat {EHB} = \widehat {IAB}\)

\(\widehat {HIE} = \widehat {AIB}\) (đối đỉnh)

\(∆ HIE \backsim ∆ AIB\) (g.g)

Suy ra: \(\frac{{HI}}{{AI}} = \frac{{HE}}{{AB}} \Rightarrow AB.HI = AI.HE\) (đpcm).

d)

Do M là điểm đối xứng với I qua AB nên:

\(\widehat {IAB} = \widehat {MAB}\)

Mà \(\widehat {IAB} = \widehat {IHE}\) (do ) nên:

\(\widehat {MAB} = \widehat {IHE}\) (1)

Tương tự ta chứng minh được: \(\widehat {HEI} = \widehat {ABM}\)(2)

Từ (1) và (2) suy ra:  (g.g) theo tỉ số \(k = \frac{{AB}}{{HE}}\)

=> \(\frac{{{S_{AMB}}}}{{{S_{HIE}}}} = {k^2} \Rightarrow {S_{AMB}} = {k^2}.{S_{HIE}}\)

Mà  cũng theo tỉ số \(k = \frac{{AB}}{{HE}}\)

=> \(\frac{{{S_{ABC}}}}{{{S_{EHC}}}} = {k^2} \Rightarrow {S_{ABC}} = {k^2}.{S_{EHC}}\)

Suy ra:

 \(\begin{array}{l}{S_{MACB}} = {S_{AMB}} + {S_{ABC}}\\ = {k^2}.{S_{HIE}} + {k^2}.{S_{EHC}}\\ = {k^2}.({S_{HIE}} + {S_{EHC}})\\ = {k^2}.{S_{IHCE}}\end{array}\)

Mà theo đề bài \({S_{MACB}} = 4.{S_{IHCE}}\)

=> \(k = 2\)

Suy ra theo tỉ số \(k = 2\)

\( \Rightarrow \frac{{BC}}{{HC}} = 2 \Rightarrow HC = \frac{{BC}}{2}\)

Vậy khi HC bằng nửa BC thì diện tích tứ giác MACB gấp 4 lần diện tích tứ giác IHCE.

Loigiaihay.com