Đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 PGD huyện Ba Vì

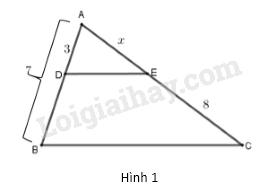
Đề bài

Bài 1: (2 điểm)

Khoanh tròn vào chữ cái A, B, C, D đứng trước câu trả lời đúng trong các câu sau.

Câu 1. Nghiệm của phương trình \(5\left( {x - 5} \right) = 20\) là

A. \(1\)                         B. \(8\)

C. \(9\)             D. \(24\)

Câu 2. Giải phương trình \(\left( {3 - 2x} \right)\left( {x + 3} \right) = 0\) ta được tập nghiệm là:

A. \(S = \left\{ {3;\dfrac{3}{2}} \right\}\)

B. \(S = \left\{ { - 3;\dfrac{3}{2}} \right\}\)

C. \(S = \left\{ {3; - \dfrac{3}{2}} \right\}\)

D. \(S = \left\{ { - 3; - \dfrac{3}{2}} \right\}\)

Câu 3. Điều kiện xác định của phương trình \(\dfrac{{2x - 3}}{{x + 1}} + \dfrac{{3x - 1}}{x} = 5\) là:

A. \(x \ne  - 1\)

B. \(x \ne 0\)

C. \(x \ne 1\) hoặc \(x \ne 0\)

D. \(x \ne  - 1\) và \(x \ne 0\)

Câu 4. Tìm \(x\) để \(\dfrac{{3x - 8}}{5}\) là số âm, ta được kết quả đúng là:

A. \(x >  - \dfrac{8}{3}\)

B. \(x < \dfrac{8}{3}\)

C. \(x > \dfrac{8}{3}\)

D. \(x <  - \dfrac{8}{3}\)

Câu 5. Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức \(\left| {x - 4} \right| + x + 1\) khi \(x \ge 4\), ta được

A. \(2x - 3\)

B. \(2x + 3\)

C. \(5\)

D. \( - 3\)

Câu 6. Trên hình 1, có \(DE//BC\), \(AD = 3,AB = 7,EC = 8\). Như vậy độ dài đoạn thẳng \(x\) bằng

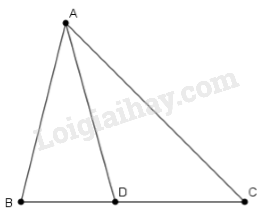
A. \(x = 6\) 

B. \(x = 5\)

C. \(x = 4\)

D. \(x = 3\)

Câu 7. Tam giác \(ABC\) có \(AB = 3,AC = 5\), \(AD\) là phân giác của góc \(BAC\) (\(D \in BC\)). Khi đó tỉ số \(\dfrac{{BD}}{{DC}}\) là tỉ số nào dưới đây?

A. \(\dfrac{{BD}}{{DC}} = \dfrac{3}{8}\)

B. \(\dfrac{{BD}}{{DC}} = \dfrac{8}{3}\)

C. \(\dfrac{{BD}}{{DC}} = \dfrac{3}{5}\)

D. \(\dfrac{{BD}}{{DC}} = \dfrac{5}{3}\)

Câu 8. Cho hình lập phương có cạnh bằng \(5\,\,cm\), thể tích của hình lập phương đó là:

A. \(125\,\,c{m^2}\)

B. \(25\,\,c{m^3}\)

C. \(25\,\,c{m^2}\)

D. \(125\,\,c{m^3}\)

Bài 2 (2,5 điểm).

1) Giải bất phương trình: \(3 - \dfrac{{x - 1}}{2} < x - 2\)

2) Giải các phương trình sau:

a) \(\dfrac{{2x}}{{{x^2} - 6x}} = \dfrac{{4\left( {3 - 2x} \right)}}{{x\left( {6 - x} \right)}}\)

b) \(\dfrac{{\left| {x - 5} \right|}}{3} = 2\)

Bài 3: (2 điểm)

Anh Sơn lái xe ô tô khởi hành từ A lúc 6h15 phút với vận tốc trung bình 50km/h. Khi đến B, anh Sơn liên hệ công tác trong thời gian 1h30 phút rồi trở về A với vận tốc trung bình 40km/h. Về đến A lúc 14h30 phút. Hỏi quãng đường AB dài bao nhiêu?

Bài 4: (3 điểm)

Cho hình thang ABCD vuông tại A, đáy nhỏ AB, đường chéo DB vuông góc với cạnh bên BC tại B. Chứng minh:

a) \(\Delta ADB\) đồng dạng với \(\Delta BCD\).

b) \(B{D^2} = AB.DC\).

c) Đường chéo \(AC\) cắt \(BD\) tại \(O\), so sánh diện tích \(\Delta AOD\) và diện tích \(\Delta BOC\)

Bài 5: (0,5 điểm)

Cho \(a,b,c\) là các số dương. Chứng minh rằng \(\left( {{a^2} + {b^2}} \right)c + \left( {{b^2} + {c^2}} \right)a + \left( {{c^2} + {a^2}} \right)b \ge 6abc\).

LG bài 1

Câu 1 (NB):

Phương pháp:

Đưa về giải phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\) \( \Leftrightarrow x =  - \dfrac{b}{a}\)

Cách giải:

Ta có:

\(\begin{array}{l}5\left( {x - 5} \right) = 20\\ \Leftrightarrow x - 5 = 4\\ \Leftrightarrow x = 5 + 4\\ \Leftrightarrow x = 9\end{array}\)

Vậy phương trình có nghiệm \(x = 9.\)

Chọn C

Câu 2 (TH):

Phương pháp:

Đưa về giải phương trình dạng \(A\left( x \right).B\left( x \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)

Cách giải:

Ta có: \(\left( {3 - 2x} \right)\left( {x + 3} \right) = 0\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3 - 2x = 0\\x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2x = 3\\x =  - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{3}{2}\\x =  - 3\end{array} \right.\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {\dfrac{3}{2}; - 3} \right\}\)

Chọn B

Câu 3 (NB):

Phương pháp:

Phân thức \(\dfrac{{A\left( x \right)}}{{B\left( x \right)}}\) xác định khi \(B\left( x \right) \ne 0\)

Cách giải:

Điều kiện xác định: \(\left\{ \begin{array}{l}x + 1 \ne 0\\x \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne  - 1\\x \ne 0\end{array} \right.\)

Vậy điều kiện xác định của phương trình là \(x \ne  - 1\) và \(x \ne 0\)

Chọn D

Câu 4 (TH):

Phương pháp:

Sử dụng \(\dfrac{A}{B} < 0\) khi \(A,B\) trái dấu.

Cách giải:

Để \(\dfrac{{3x - 8}}{5}\) là số âm, tức là \(\dfrac{{3x - 8}}{5} < 0\) thì \(3x - 8 < 0\) (do \(5 > 0\))

Ta có \(3x - 8 < 0\) \( \Leftrightarrow 3x < 8 \Leftrightarrow x < \dfrac{8}{3}\)

Chọn B

Câu 5 (TH):

Phương pháp:

Sử dụng \(\left| A \right| = A\) nếu \(A \ge 0\)

Cách giải:

Với \(x \ge 4\) thì \(x - 4 \ge 0\) nên \(\left| {x - 4} \right| = x - 4\)

Do đó: \(\left| {x - 4} \right| + x + 1\)\( = x - 4 + x + 1\) \( = 2x - 3\)

Chọn A

Câu 6 (TH):

Phương pháp:

Sử dụng định lý Ta-lét trong tam giác

Cách giải:

Ta có: \(AD + DB = AB\) \( \Leftrightarrow BD = AB - AD\) \( = 7 - 3 = 4\)

Xét \(\Delta ABC\) có \(DE//BC\), theo định lý Ta-lét ta có:

\(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{EC}}\) \( \Leftrightarrow \dfrac{3}{4} = \dfrac{x}{8}\) \( \Leftrightarrow 4x = 3.8 \Leftrightarrow x = 6\)

Chọn A

Câu 7 (TH):

Phương pháp:

Sử dụng tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tương ứng tỉ lệ với hai cạnh kề hai đoạn đó .

Cách giải:

Xét tam giác ABC có AD là phân giác góc A, theo tính chất đường phân giác của tam giác ta có:

 \(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}\) \( = \dfrac{3}{5}\)

Chọn C 

Câu 8 (TH):

Phương pháp:

Sử dụng thể tích hình lập phương cạnh \(a\) là  \(V = {a^3}\)

Cách giải:

Thể tích hình lập phương là: \(V = {5^3} = 125c{m^3}\)

Chọn D

LG bài 2

Phương pháp giải:

1) Qui đồng rồi đưa về giải bất phương trình bậc nhất một ẩn

2) a) Giải phương trình chứa ẩn ở mẫu

B1: Tìm điều kiện xác định

B2: Qui đồng mẫu và khử mẫu

B3: Giải phương trình thu được 

B4: So sánh điều kiện và kết luận nghiệm

b) Đưa về dạng \(\left| {A\left( x \right)} \right| = m\left( {m \ge 0} \right)\)

Sau đó phá dấu giá trị tuyệt đối để tìm \(x.\)

Lời giải chi tiết:

1) \(3 - \dfrac{{x - 1}}{2} < x - 2\)

\(\begin{array}{l} \Leftrightarrow \dfrac{6}{2} - \dfrac{{x - 1}}{2} < \dfrac{{2x}}{2} - \dfrac{4}{2}\\ \Leftrightarrow 6 - \left( {x - 1} \right) < 2x - 4\\ \Leftrightarrow 6 - x + 1 < 2x - 4\\ \Leftrightarrow  - x - 2x <  - 6 - 1 - 4\\ \Leftrightarrow  - 3x <  - 11\\ \Leftrightarrow x > \dfrac{{11}}{3}\end{array}\)

Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x|x > \dfrac{{11}}{3}} \right\}\)

2) a) \(\dfrac{{2x}}{{{x^2} - 6x}} = \dfrac{{4\left( {3 - 2x} \right)}}{{x\left( {6 - x} \right)}}\) 

Điều kiện: \(x \ne 0;x \ne 6\)

\(\dfrac{{2x}}{{{x^2} - 6x}} = \dfrac{{4\left( {3 - 2x} \right)}}{{x\left( {6 - x} \right)}}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{2x}}{{x\left( {x - 6} \right)}} = \dfrac{{ - 4\left( {3 - 2x} \right)}}{{x\left( {x - 6} \right)}}\\ \Rightarrow 2x =  - 4\left( {3 - 2x} \right)\\ \Leftrightarrow 2x =  - 12 + 8x\\ \Leftrightarrow 2x - 8x =  - 12\\ \Leftrightarrow  - 6x =  - 12\end{array}\)

\( \Leftrightarrow x = 2\) (thỏa mãn điều kiện)

Vậy phương trình có nghiệm \(x = 2.\)

b) \(\dfrac{{\left| {x - 5} \right|}}{3} = 2\)

\( \Leftrightarrow \left| {x - 5} \right| = 6\)

TH1: \(\left| {x - 5} \right| = x - 5\) với \(x - 5 \ge 0 \Leftrightarrow x \ge 5\) 

Ta có phương trình \(x - 5 = 6 \Leftrightarrow x = 11\) (thỏa mãn)

TH2: \(\left| {x - 5} \right| = 5 - x\) với \(x - 5 < 0 \Leftrightarrow x < 5\)

Ta có phương trình \(5 - x = 6\)\( \Leftrightarrow  - x = 6 - 5\)\( \Leftrightarrow x =  - 1\)  (thỏa mãn)

Vậy phương trình có tập nghiệm \(S = \left\{ { - 1;11} \right\}\)

LG bài 3

Phương pháp giải:

Giải bài toán bằng cách lập phương trình

B1: Chọn ẩn và đặt điều kiện cho ẩn

B2: Lập phương trình và giải phương trình

B3: So sánh điều kiện và kết luận nghiệm

Lời giải chi tiết:

Anh Sơn lái xe ô tô khởi hành từ A lúc 6h15 phút với vận tốc trung bình 50km/h. Khi đến B, anh Sơn liên hệ công tác trong thời gian 1h30 phút rồi trở về A với vận tốc trung bình 40km/h. Về đến A lúc 14h30 phút. Hỏi quãng đường AB dài bao nhiêu?

Gọi quãng đường AB là \(x\) (km) \(\left( {x > 0} \right)\)

Thời gian anh Sơn đi từ A đến B là \(\dfrac{x}{{50}}\) giờ

Thời gian anh Sơn đi từ B về A là \(\dfrac{x}{{40}}\) giờ

Vì anh khởi hành lúc 6h15 phút và trở về A lúc 14h30 phút, đồng thời liên hệ công tác mất 1h30 phút nên tổng thời gian anh đi trên đường là:

14h30 phút -6h15 phút-1h30 phút = 6 giờ 45 phút \( = \dfrac{{27}}{4}\) giờ

Ta có phương trình: \(\dfrac{x}{{50}} + \dfrac{x}{{40}} = \dfrac{{27}}{4}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{4x + 5x}}{{200}} = \dfrac{{27.50}}{{200}}\\ \Leftrightarrow 9x = 27.50\end{array}\) 

\( \Leftrightarrow x = 150\) (thoả mãn)

Vậy quãng đường AB dài 150km.

LG bài 4

Phương pháp giải:

a) Chứng minh hai tam giác theo trường hợp góc – góc.

b) Từ câu a suy ra cặp cạnh tương ứng tỉ lệ.

c) Kẻ \(BK \bot DC\), chứng minh \({S_{ADC}} = {S_{BDC}}\), từ đó sử dụng phương pháp cộng trừ diện tích để so sánh \({S_{AOD}}\) và \({S_{BOC}}\).

Lời giải chi tiết:

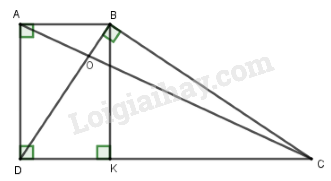
a) \(\Delta ADB\) đồng dạng với \(\Delta BCD\).

ABCD là hình thang đáy AB, CD nên \(AB//CD\)

\( \Rightarrow \widehat {ABD} = \widehat {BDC}\) (so le trong)

Xét \(\Delta ADB\) và \(\Delta BCD\) có:

\(\begin{array}{l}\widehat {DAB} = \widehat {DBC} = {90^0}\\\widehat {ABD} = \widehat {BDC}\left( {cmt} \right)\\ \Rightarrow \Delta ADB \sim \Delta BCD\left( {g - g} \right)\end{array}\)

b) \(B{D^2} = AB.DC\).

Từ câu a, \(\Delta ADB \sim \Delta BCD\) \( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{DB}}{{CD}}\) (cạnh tương ứng)

\( \Rightarrow AB.CD = B{D^2}\) (đpcm)

c) Đường chéo \(AC\) cắt \(BD\) tại \(O\), so sánh diện tích \(\Delta AOD\) và diện tích \(\Delta BOC\)

Kẻ \(BK \bot DC\) (K thuộc DC).

Tứ giác ABKD có \(\widehat A = \widehat D = \widehat K = {90^0}\) nên là hình chữ nhật (tứ giác có ba góc vuông)

\( \Rightarrow AD = BK\).

Ta có:

\(\begin{array}{l}{S_{ADC}} = \dfrac{1}{2}AD.DC\\{S_{BDC}} = \dfrac{1}{2}BK.DC\end{array}\)

Mà \(AD = BK\left( {cmt} \right)\) và \(DC = DC\) nên \({S_{ADC}} = {S_{BDC}}\)

\(\begin{array}{l} \Rightarrow {S_{AOD}} + {S_{ODC}} = {S_{OBC}} + {S_{ODC}}\\ \Rightarrow {S_{AOD}} = {S_{OBC}}\end{array}\)

Vậy \({S_{AOD}} = {S_{BOC}}\).

LG bài 5

Phương pháp giải:

Sử dụng bất đẳng thức \({x^2} + {y^2} \ge 2xy\)

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}{\left( {a - b} \right)^2} \ge 0 \Rightarrow {a^2} - 2ab + {b^2} \ge 0\\ \Rightarrow {a^2} + {b^2} \ge 2ab\end{array}\)

Tương tự,

\(\begin{array}{l}{b^2} + {c^2} \ge 2bc\\{c^2} + {a^2} \ge 2ca\end{array}\)

\(\begin{array}{l} \Rightarrow \left( {{a^2} + {b^2}} \right)c + \left( {{b^2} + {c^2}} \right)a + \left( {{c^2} + {a^2}} \right)b\\ \ge 2ab.c + 2bc.a + 2ca.b\\ = 2abc + 2abc + 2abc\\ = 6abc\end{array}\)

\( \Rightarrow \left( {{a^2} + {b^2}} \right)c + \left( {{b^2} + {c^2}} \right)a\)\( + \left( {{c^2} + {a^2}} \right)b \ge 6abc\)

Dấu “=” xảy ra khi \(a = b = c\).

HẾT

Loigiaihay.com