Đề kiểm tra giữa kì II Toán 8 - Đề số 2 có lời giải chi tiếtĐề kiểm tra giữa kì 2 toán 8 - Đề số 2 có lời giải chi tiết Quảng cáo
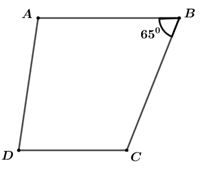
Đề bài Câu 1. Kết quả của phép nhân \(\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)\) là A. \({x^3} - 1\) B. \({x^3} + 1\) C. \({x^3} - 3{x^2} + 3x - 1\) D. \({x^3} + 3{x^2} + 3x + 1\) Câu 2. Khai triển hằng đẳng thức \({\left( {\frac{1}{2} + 2x} \right)^2}\) ta được kết quả là: A. \(\frac{1}{4} + 4{x^2}\) B. \(\frac{1}{4} + 4x + 4{x^2}\) C. \(\frac{1}{4} + 2x + 2{x^2}\) D. \(\frac{1}{4} + 2x + 4{x^2}\) Câu 3. Trong các khẳng định sau, khẳng định nào không đúng? A. Hình thang có hai cạnh bên bằng nhau là hình thang cân. B. Hình thang có hai đường chéo bằng nhau là hình thang cân. C. Hình thang có hai cạnh bên song song là hình bình hành. D. Hình thang cân có một góc vuông là hình chữ nhật. Câu 4. Kết quả của phép chia \(\left( {{x^2} - 6x + 9} \right):\left( {x - 3} \right)\) là A. \(x + 3\) B. \(x - 3\) C. \({\left( {x + 3} \right)^2}\) D. \({\left( {x - 3} \right)^2}\) Câu 5. Giá trị của biểu thức \({x^2} - 4xy + 4{y^2}\) tại \(x = - 8\) và \(y = 1\) là: A. \(36\) B. \( - 36\) C. \(100\) D. \( - 100\) Câu 6. Cho hình thang \(ABCD\left( {AB\,{\rm{//}}\,CD} \right)\) biết \(\angle B = {65^0}\). Số đo góc \(C\) bằng:
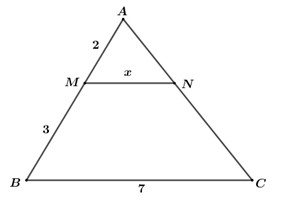
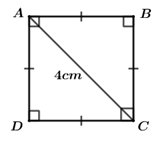
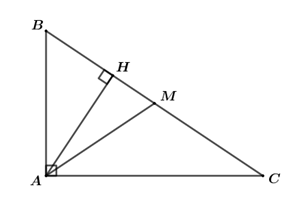
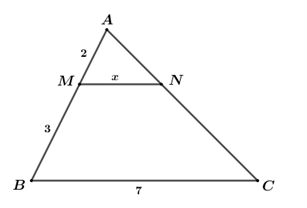
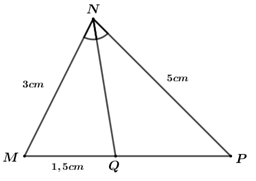
Câu 7. Giá trị của biểu thức \(x\left( {x - y} \right) - y\left( {y - x} \right)\) tại \(x = 2\) và \(y = - 3\) là A. \(5\) B. \( - 5\) C. \(13\) D. \( - 13\) Câu 8. Giá trị của \(x\) thỏa mãn phương trình \({x^3} + 4x = 0\) là A. \(x = 0\) B. \(x = 0;\,\,x = 2\) C. \(x = 0;\,\,x = - 2\) D. \(x = 0;\,\,x = \pm 2\) Câu 9. Hình vuông có đường chéo bằng \(4cm\), cạnh của hình vuông đó bằng: A. \(4\,\,cm\) B. \(8\,\,cm\) C. \(\sqrt 8 \,\,cm\) D. \(2\,\,cm\) Câu 10. Kết quả phân tích đa thức \({x^2} - 3x + 2\) thành nhân tử là A. \(\left( {x - 1} \right)\left( {x + 2} \right)\) B. \(\left( {x - 1} \right)\left( {x - 2} \right)\) C. \(\left( {x + 1} \right)\left( {x - 2} \right)\) D. \(\left( {x + 1} \right)\left( {x + 2} \right)\) Câu 11. Biểu thức \(\frac{{2x}}{{{x^2} - 1}}\) xác định với các giá trị của \(x\) thỏa mãn: A. \(x \ne 0,\,\,x \ne \pm 1\) B. \(x \ne 1\) C. \(x \ne - 1\) D. \(x \ne \pm 1\) Câu 12. Trong các hình sau đây, hình nào không có trục đối xứng? A. Hình thang cân B. Hình bình hành C. Hình chữ nhật D. Hình thoi Câu 13. Giá trị của biểu thức \({x^3} - 9{x^2} + 27x - 27\) khi \(x = 5\) là: A. \(3\) B. \(6\) C. \(8\) D. \(9\) Câu 14. Nghiệm của phương trình \(\frac{{x - 2}}{4} = \frac{{2x - 4}}{3}\) là: A. \(x = 3\) B. \(x = - 3\) C. \(x = 2\) D. \(x = - 2\) Câu 15. Hình bình hành có hai đường chéo bằng nhau là: A. Hình thang cân B. Hình chữ nhật C. Hình thoi D. Hình vuông Câu 16. Kết quả phân tích đa thức \({x^2} - x + y - {y^2}\) được phân tích thành nhân tử là: A. \(\left( {x - y} \right)\left( {x - 1} \right)\) B. \(\left( {x - y} \right)\left( {x - 1} \right)\) C. \(\left( {x - 1} \right)\left( {y - 1} \right)\) D. \(\left( {x - y} \right)\left( {x + y - 1} \right)\) Câu 17. Trong một cuộc thi, mỗi thí sinh phải trả lời \(10\) câu hỏi. Mỗi câu trả lời đúng được \(10\) điểm, mỗi câu trả lời sai bị trừ \(5\) điểm. Một học sinh được tất cả \(70\) điểm. Hỏi bạn ấy đã trả lời đúng mấy câu? A. \(6\) câu B. \(7\) câu C. \(8\) câu D. \(9\) câu Câu 18. Hai đường chéo của một hình thoi bằng \(6cm\) và \(10cm\). Diện tích của hình thoi đó bằng: A. \(30c{m^2}\) B. \(60c{m^2}\) C. \(32c{m^2}\) D. \(16c{m^2}\) Câu 19. Với mọi \(x \in \mathbb{R}\) phát biểu nào sau đây là sai? A. \({x^2} - 2x + 3 > 0\) B. \(6x - {x^2} - 10 < 0\) C. \({x^2} - x - 100 < 0\) D. \({x^2} - x + 1 > 0\) Câu 20. Phương trình \(\frac{{{x^2} - 5x}}{{x - 5}} = 5\) có tập nghiệm là: A. \(S = \left\{ 5 \right\}\) B. \(S = \emptyset \) C. \(S = \left\{ 0 \right\}\) D. \(S = \mathbb{R}\) Câu 21. Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH = 12cm\) và đường trung tuyến \(AM = 15cm\). Khẳng định nào sau đây là đúng? A. \(\frac{{AB}}{{AC}} = \frac{3}{5}\) B. \(\frac{{AB}}{{AC}} = \frac{2}{3}\) C. \(\frac{{AB}}{{AC}} = \frac{3}{4}\) D. \(\frac{{AB}}{{AC}} = \frac{1}{2}\) Câu 22. Kết quả của phép tính \(\frac{{4{x^2}}}{{5{y^2}}}:\frac{{6x}}{{5y}}\) bằng: A. \(\frac{2}{{3y}}\) B. \(\frac{{2x}}{3}\) C. \(\frac{{2x}}{{3y}}\) D. \(\frac{2}{3}\) Câu 23. Rút gọn biểu thức \(P = \frac{{x + 4}}{{{x^2} - 4}} - \frac{1}{{{x^2} + 2x}}\) ta được kết quả là: A. \(\frac{{{x^2} + 3x + 2}}{{x\left( {{x^2} - 4} \right)}}\) B. \(\frac{{x + 1}}{{x\left( {x - 2} \right)}}\) C. \(\frac{{{x^2} - 3x - 2}}{{x\left( {{x^2} - 4} \right)}}\) D. \(\frac{{x - 1}}{{x\left( {x - 2} \right)}}\) Câu 24. Cho hình vẽ \(\left( {MN\,{\rm{//}}\,BC} \right)\). Khi đó \(x\) bằng: A. \(\frac{{14}}{3}\) B. \(\frac{9}{5}\) C. \(2,8\) D. \(3,2\) Câu 25. Đa thức \(P\) trong đẳng thức \(\frac{{x - 2}}{{{x^2} + 4}} = \frac{{2{x^2} - 4x}}{P}\) là A. \(2{x^2} - 8x\) B. \(2{x^2} + 8x\) C. \(2{x^3} - 8x\) D. \(2{x^3} + 8x\) Câu 26. Giá trị của biểu thức \(\frac{{9{x^2} - 16}}{{3{x^2} - 4x}}\) tại \(x = - 4\) là: A. \( - 2\) B. \(2\) C. \(4\) D. \( - 4\) Câu 27. Cho \(\Delta MNP\) có \(NQ\) là tia phân giác của góc \(MNP\). Biết \(MN = 3cm;\,\)\(NP = 5cm;\,\,\)\(MQ = 1,5cm\). Độ dài đoạn \(PQ\) bằng A. \(2,5cm\) B. \(3,5cm\) C. \(4cm\) D. \(4,5cm\) Câu 28. Trong các đẳng thức sau, đẳng thức nào không đúng? A. \(\frac{{{x^3}{y^3}}}{{x{y^4}}} = \frac{{{x^2}}}{y}\) B. \(\frac{{{x^2} - {y^2}}}{{x - y}} = x + y\) B. C. \(\frac{{{x^2} + {y^2}}}{{{y^2}}} = {x^2}\) D. \(\frac{{16{x^2}y\left( {y + x} \right)}}{{12xy\left( {x + y} \right)}} = \frac{{4x}}{3}\) Câu 29. Rút gọn phân thức \(\frac{{{x^5} + {x^4} + 1}}{{{x^2} + x + 1}}\) ta được kết quả là: A. \({x^3} - {x^2} + 1\) B. \({x^3} - {x^2} - 1\) B. C. \({x^3} + {x^2} - 1\) D. \({x^3} - x + 1\) Câu 30. Biết tam giác \(MNP\) đồng dạng với tam giác \(PQR\). Hệ thức nào sau đây không đúng? A. \(MN.QR = NP.PQ\) B. \(MP.QR = NP.PR\) C. \(MN.PQ = NP.QR\) D. \(MN.PR = MP.PQ\) Lời giải chi tiết
Câu 1 (NB): Phương pháp: Áp dụng hằng đẳng thức “Tổng hai lập phương”: \({A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)\) Cách giải: Ta có: \(\left( {{x^2} - x + 1} \right)\left( {x + 1} \right)\)\( = \left( {x + 1} \right).\left( {{x^2} - 1.x + {1^2}} \right)\)\( = {x^3} + 1\) Chọn B. Câu 2 (NB): Phương pháp: Áp dụng hằng đẳng thức “Bình phương của một tổng”: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Cách giải: Ta có: \({\left( {\frac{1}{2} + 2x} \right)^2}\)\( = {\left( {\frac{1}{2}} \right)^2} + 2 \cdot \frac{1}{2} \cdot 2x + {\left( {2x} \right)^2}\)\( = \frac{1}{4} + 2x + 4{x^2}\) Chọn D. Câu 3 (TH): Phương pháp: Áp dụng dấu hiệu nhận biết của hình thang cân, hình bình hành, hình chữ nhật. Cách giải: Theo dấu hiệu nhận biết, ta có: + Hình thang có hai đường chéo bằng nhau là hình thang cân. + Hình thang có hai cạnh bên song song là hình bình hành. + Hình thang có một góc vuông là hình chữ nhật Vậy khẳng định không đúng là: Hình thang có hai cạnh bên bằng nhau. Chọn A. Câu 4 (TH): Phương pháp: Áp dụng hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) để đưa đa thức bị chia về dạng gọn hơn. Áp dụng quy tắc chia đa thức cho đơn thức. Cách giải: Ta có: \(\left( {{x^2} - 6x + 9} \right):\left( {x - 3} \right)\) \( = {\left( {x - 3} \right)^2}:\left( {x - 3} \right)\)\( = \left( {x - 3} \right)\) Chọn B. Câu 5 (TH): Phương pháp: Áp dụng hằng đẳng thức để rút gọn biểu thức. Sau đó, thay các giá trị của \(x\) và \(y\) vào biểu thức vừa thu gọn để tính giá trị biểu thức. Cách giải: \({x^2} - 4xy + 4{y^2}\)\( = {x^2} - 2.x.2y + {\left( {2y} \right)^2}\)\( = {\left( {x - 2y} \right)^2}\) Thay \(x = - 8\) và \(y = 1\) vào \({\left( {x - 2y} \right)^2}\) ta được: \({\left( { - 8 - 2.1} \right)^2}\)\( = {\left( { - 8 - 2} \right)^2}\)\( = {\left( { - 10} \right)^2}\)\( = 100.\) Chọn C. Câu 6 (TH): Phương pháp: Áp dụng định nghĩa hình thang: Hình thang là tứ giác có hai cạnh đối song song Cách giải: Vì \(ABCD\) là hình thang nên \(AB\,{\rm{//}}\,CD\). \( \Rightarrow \angle B + \angle C = {180^0}\) (hai góc trong cùng phía bù nhau) \( \Rightarrow \angle C = {180^0} - \angle B\) \( \Rightarrow \angle C = {180^0} - {65^0}\) \( \Rightarrow \angle C = {115^0}\) Vậy số đo góc \(C\) bằng \({115^0}\). Chọn D. Câu 7 (TH): Phương pháp: Áp dụng hẳng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để rút gọn biểu thức. Sau đó, thay giá trị của \(x\) và \(y\) vào biểu thức vừa thu gọn để tính giá trị của biểu thức. Cách giải: Rút gọn biểu thức \(x\left( {x - y} \right) - y\left( {y - x} \right)\). \(\begin{array}{l}x\left( {x - y} \right) - y\left( {y - x} \right)\\ = x\left( {x - y} \right) + y\left( {x - y} \right)\\ = \left( {x + y} \right)\left( {x - y} \right)\\ = {x^2} - {y^2}\end{array}\) Thay \(x = 2\) và \(y = - 3\) vào biểu thức \({x^2} - {y^2}\) ta được: \({2^2} - {\left( { - 3} \right)^2} = 4 - 9 = - 5\) Chọn B. Câu 8 (TH): Phương pháp: Áp dụng phương pháp đặt nhân tử chung để đưa về phương trình tích. Cách giải phương trình tích: \(A\left( x \right).B\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\) Cách giải: \(\begin{array}{l}\,\,\,\,\,\,\,{x^3} + 4x = 0\\ \Leftrightarrow x\left( {{x^2} + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 4 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {tm} \right)\\{x^2} = - 4 < 0\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy giá trị của \(x\) thỏa mãn phương trình \({x^3} + 4x = 0\) là \(x = 0\). Chọn A. Câu 9 (TH): Phương pháp: Áp dụng định nghĩa hình vuông và định lý Py-ta-go để tìm độ dài cạnh của hình vuông. Cách giải: Giả sử hình vuông \(ABCD\) có độ dài đường chéo \(AC\) bằng \(4cm\). Vì \(ABCD\) là hình vuông nên ta có: \(\left\{ \begin{array}{l}AB = BC = CD = DA\\\angle A = \angle B = \angle C = \angle D = {90^0}\end{array} \right.\) Xét \(\Delta ABC\) vuông tại \(B\), áp dụng định lý Py-ta-go ta có: \(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}\\ \Rightarrow A{C^2} = A{B^2} + A{B^2}\left( {{\mathop{\rm vì}\nolimits} \,AB = BC} \right)\\ \Rightarrow A{C^2} = 2A{B^2}\\ \Rightarrow A{B^2} = \frac{{A{C^2}}}{2}\\ \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 = \sqrt 8 \,\,\left( {cm} \right)\end{array}\) Vậy cạnh của hình vuông đó bằng \(\sqrt 8 \left( {cm} \right)\). Chọn C. Câu 10 (TH): Phương pháp: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp: phương pháp tách, nhóm và đặt nhân tử chung. Cách giải: \(\begin{array}{l}\,\,\,\,\,{x^2} - 3x + 2\\ = {x^2} - x - 2x + 2\\ = \left( {{x^2} - x} \right) - \left( {2x - 2} \right)\\ = x\left( {x - 1} \right) - 2\left( {x - 1} \right)\\ = \left( {x - 2} \right)\left( {x - 1} \right)\end{array}\) Vậy \({x^2} - 3x + 2 = \left( {x - 1} \right)\left( {x - 2} \right)\). Chọn B. Câu 11 (NB): Phương pháp: Biểu thức \(\frac{{A\left( x \right)}}{{B\left( x \right)}}\) xác định khi và chỉ khi \(B \ne 0\). Cách giải: Biểu thức \(\frac{{2x}}{{{x^2} - 1}}\) xác định khi \({x^2} - 1 \ne 0\)\( \Leftrightarrow {x^2} \ne 1 \Leftrightarrow x \ne \pm 1\). Chọn D. Câu 12 (TH): Phương pháp: Áp dụng định nghĩa “Hình có trục đối xứng”: Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H\). Cách giải: *) Xét đáp án A Hình thang cân có \(1\) trục đối xứng là đường thẳng đi qua trung điểm hai đáy của hình thang cân. *) Xét đáp án B: Hình bình hành không có trục đối xứng. *) Xét đáp án C: Hình chữ nhật có \(2\) trục đối xứng là hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình chữ nhật. *) Xét đáp án D Hình thoi có \(2\) trục đối xứng là hai đường chéo của hình thoi. Vậy hình có trục đối xứng là: Hình bình hành Chọn B. Câu 13 (TH): Phương pháp: Áp dụng hằng đẳng thức “Lập phương của một hiệu”: \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) Thay giá trị của \(x\) vào biểu thức vừa thu gọn được để tính giá trị của biểu thức. Cách giải: Ta có: \(\begin{array}{l}\,\,\,\,{x^3} - 9{x^2} + 27x - 27\\ = {x^3} - 3.{x^2}.3 + 3.x{.3^2} - {3^3}\\ = {\left( {x - 3} \right)^3}\end{array}\) Thay \(x = 5\) vào biểu thức \({\left( {x - 3} \right)^3}\) ta được: \({\left( {5 - 3} \right)^3} = {2^3} = 8\) Chọn C. Câu 14 (TH): Phương pháp: Đây là phương trình không chứa ẩn ở mẫu nên đưa phương trình về dạng \(ax + b = 0\) hay \(ax = - b\). Cách giải: \(\begin{array}{l}\,\,\,\,\,\,\,\frac{{x - 2}}{4} = \frac{{2x - 4}}{3}\\ \Rightarrow 3\left( {x - 2} \right) = \left( {2x - 4} \right).4\\ \Leftrightarrow 3x - 6 = 8x - 16\\ \Leftrightarrow 3x - 8x = - 16 + 6\\ \Leftrightarrow - 5x = - 10\\ \Leftrightarrow x = 2\end{array}\) Vậy tập nghiệm của phương trình \(\frac{{x - 2}}{4} = \frac{{2x - 4}}{3}\) là \(x = 2\). Chọn C. Câu 15 (TH): Phương pháp: Áp dụng dấu hiệu nhận biết của các hình. Cách giải: Theo dấu hiệu nhận biết hình chữ nhật: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật. Chọn B. Câu 16 (VD): Phương pháp: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp: Nhóm hạng tử, dùng hằng đẳng thức, đặt nhân tử chung. Cách giải: \(\begin{array}{l}\,\,\,\,\,{x^2} - x + y - {y^2}\\ = \left( {{x^2} - {y^2}} \right) - \left( {x - y} \right)\\ = \left( {x - y} \right)\left( {x + y} \right) - \left( {x - y} \right)\\ = \left( {x - y} \right)\left[ {\left( {x + y} \right) - 1} \right]\\ = \left( {x - y} \right)\left( {x + y - 1} \right)\end{array}\) Chọn D. Câu 17 (VD): Phương pháp: Các bước giải bài toán bằng cách lập phương trình: Bước 1: Lập phương trình - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình Bước 3: Kết hợp với điều kiện xác định và kết luận. Cách giải: Gọi số câu trả lời đúng là \(x\) (câu) (\(x \in {\mathbb{N}^*}\)). Số câu trả lời sai là: \(10 - x\) (câu) Số điểm đạt được khi trả lời đúng là: \(10x\) (điểm) Số điểm bị trừ khi trả lời sai là: \(5\left( {10 - x} \right)\) (điểm) Vì một học sinh được tất cả \(70\) điểm nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\,10x - 5\left( {10 - x} \right) = 70\\ \Leftrightarrow 10x - 50 + 5x = 70\\ \Leftrightarrow 15x = 120\\ \Leftrightarrow x = 120:15\\ \Leftrightarrow x = 8\,\,\left( {tm} \right)\end{array}\) Vậy học sinh đó đã trả lời đúng \(8\) câu. Chọn C. Câu 18 (NB): Phương pháp: Diện tích hình thoi bằng nửa tích hai đường chéo. Cách giải: Diện tích của hình thoi đó là: \(\frac{{6.10}}{2} = 30\left( {c{m^2}} \right)\) Chọn A. Câu 19 (VD): Phương pháp: Biến đổi đa thức bằng cách áp dụng hằng đẳng thức để đưa biểu thức về dạng: \(A\left( x \right) = {B^2}\left( x \right) + c\) (trong đó \(c\) là hằng số) Cách giải: Xét đáp án A: \({x^2} - 2x + 3\)\( = {x^2} - 2x + 1 + 2\)\( = {\left( {x - 1} \right)^2} + 2 \ge 2 > 0\) với mọi \(x \in \mathbb{R}\) \( \Rightarrow \) Đáp án A đúng. Xét đáp án B: \(6x - {x^2} - 10\) \( = - \left( {{x^2} - 6x + 10} \right)\)\( = - \left( {{x^2} - 6x + 9 + 1} \right)x\) \( = - \left[ {{{\left( {x - 3} \right)}^2} + 1} \right]\)\( = - {\left( {x - 3} \right)^2} - 1 \le - 1 < 0\)với mọi \(x \in \mathbb{R}\) \( \Rightarrow \) Đáp án B đúng. Xét đáp án C: \({x^2} - x - 100\)\( = {x^2} - 2.x.\frac{1}{2} + \frac{1}{4} - \frac{{401}}{4}\) \( = {\left( {x - \frac{1}{2}} \right)^2} - \frac{{401}}{4} \ge - \frac{{401}}{4}\) với mọi \(x \in \mathbb{R}\). \( \Rightarrow \) Đáp án C sai. Xét đáp án D: \({x^2} - x + 1\) \( = {x^2} - 2.\frac{1}{2}.x + \frac{1}{4} + \frac{3}{4}\) \( = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4}\,\, > 0\) với mọi \(x \in \mathbb{R}\). \( \Rightarrow \) Đáp án D đúng. Chọn C. Câu 20 (VD): Phương pháp: Các bước giải phương trình chứa ẩn ở mẫu: Bước 1: Tìm điều kiện xác định của phương trình. Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu. Bước 3: Giải phương trình vừa nhận được. Bước 4 (Kết luận): Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho. Cách giải: Điều kiện: \(x \ne 5\) \(\frac{{{x^2} - 5x}}{{x - 5}} = 5\) \( \Rightarrow {x^2} - 5x = 5\left( {x - 5} \right)\) \( \Leftrightarrow {x^2} - 5x = 5x - 25\) \( \Leftrightarrow {x^2} - 10x + 25 = 0\) \( \Leftrightarrow {\left( {x - 5} \right)^2} = 0\) \( \Leftrightarrow x = 5\) Ta thấy \(x = 5\) không thỏa mãn điều kiện xác định. Vậy \(S = \emptyset \). Chọn B. Câu 21 (VD): Phương pháp: + Chứng minh tam giác đồng dạng để suy ra \(AB.AC = AH.BC\). + Áp dụng định lý Py-ta-go để có \(A{B^2} + A{C^2} = B{C^2}\). Từ đó, tính được \(A{B^2}\) và \(A{C^2}\) sau đó lập tỉ số. Cách giải: \(\Delta ABC\) vuông tại \(A\) có \(AM\) là đường trung tuyến nên \(AM = \frac{{BC}}{2}\)\( \Rightarrow BC = 2AM\)\( = 2.15 = 30\,\,\left( {cm} \right)\). Xét \(\Delta ABH\) và \(\Delta CBA\) có: \(\angle AHB = \angle BAC\,\,\left( { = {{90}^0}} \right)\) \(\angle B\) chung \( \Rightarrow \Delta ABH \sim \Delta CBA\) (góc – góc) \( \Rightarrow \frac{{AB}}{{CB}} = \frac{{AH}}{{AC}}\) (tỷ số cặp cạnh tương ứng) \(\begin{array}{l} \Leftrightarrow AB.AC = AH.BC\\ \Leftrightarrow AB.AC = 12.30\\ \Leftrightarrow AB.AC = 360\\ \Leftrightarrow AB = \frac{{360}}{{AC}}\\ \Leftrightarrow A{B^2} = \frac{{{{360}^2}}}{{A{C^2}}}\end{array}\) Xét \(\Delta ABC\) vuông tại \(A\), áp dụng định lý Py-ta-go ta có: \( \Leftrightarrow \frac{{{{360}^2}}}{{A{C^2}}} + A{C^2} = {30^2}\) \( \Leftrightarrow {360^2} + A{C^4} - 900A{C^2} = 0\) \( \Leftrightarrow A{C^4} - 900A{C^2} + {360^2} = 0\) \( \Leftrightarrow A{C^4} - 720A{C^2} - 180A{C^2} + {360^2} = 0\) \( \Leftrightarrow \left( {A{C^4} - 720A{C^2}} \right) - \left( {180A{C^2} - {{360}^2}} \right) = 0\) \(\begin{array}{l} \Leftrightarrow A{C^2}\left( {A{C^2} - 720} \right) - 180\left( {A{C^2} - 720} \right) = 0\\ \Leftrightarrow \left( {A{C^2} - 720} \right)\left( {A{C^2} - 180} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}A{C^2} - 720 = 0\\A{C^2} - 180 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}A{C^2} = 720\\A{C^2} = 180\end{array} \right.\end{array}\) Trường hợp 1: \(A{C^2} = 720\)\( \Rightarrow A{B^2} = 180\). Khi đó, ta có: \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{180}}{{720}} = \frac{1}{4}\)\( \Rightarrow \frac{{AB}}{{AC}} = \frac{1}{2}\) Trường hợp 2: \(A{C^2} = 180\)\( \Rightarrow A{B^2} = 720\). Khi đó, ta có: \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{720}}{{180}} = 4\)\( \Rightarrow \frac{{AB}}{{AC}} = 2\) Chọn D. Câu 22 (TH): Phương pháp: Áp dụng quy tắc chia phân thức đại số: \(\frac{A}{B}:\frac{C}{D} = \frac{A}{B} \cdot \frac{D}{C}\) với \(\frac{C}{D} \ne 0\) Cách giải: Ta có: \(\frac{{4{x^2}}}{{5{y^2}}}:\frac{{6x}}{{5y}} = \frac{{4{x^2}}}{{5{y^2}}} \cdot \frac{{5y}}{{6x}} = \frac{{4{x^2}.5y}}{{5{y^2}.6x}} = \frac{{2x}}{{3y}}\) Chọn C. Câu 23 (VD): Phương pháp: Áp dụng các phép toán trên tập hợp các phân thức đại số để rút gọn biểu thức. Cách giải: Ta có: \(\begin{array}{l}P = \frac{{x + 4}}{{{x^2} - 4}} - \frac{1}{{{x^2} + 2x}}\\\,\end{array}\) \(\begin{array}{l} = \frac{{x + 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{1}{{x\left( {x + 2} \right)}}\\\,\,\,\,\,\end{array}\) \(\begin{array}{l} = \frac{{x\left( {x + 4} \right) - \left( {x - 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}}\\\,\, = \frac{{{x^2} + 4x - x + 2}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \frac{{{x^2} + 3x + 2}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}}\\\,\,\,\,\, = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}}\\\,\,\,\,\, = \frac{{x + 1}}{{x\left( {x - 2} \right)}}\end{array}\) Vậy rút gọn biểu thức \(P = \frac{{x + 4}}{{{x^2} - 4}} - \frac{1}{{{x^2} + 2x}}\) ta được kết quả là \(\frac{{x + 1}}{{x\left( {x - 2} \right)}}\). Chọn B. Câu 24 (VD): Phương pháp:
Ta có: \(a\,{\rm{//}}\,BC \Rightarrow \)\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{BC'}}{{BC}}\) Cách giải: Ta có: \(AB = AM + MB = 2 + 3 = 5\) Xét \(\Delta ABC\), có \(MN\,{\rm{//}}\,BC\). Áp dụng hệ quả của định lý Ta-lét ta có: \(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}}\)\( \Rightarrow MN = \frac{{AM.BC}}{{AB}}\)\( = \frac{{2.7}}{5} = 2,8\)\( \Rightarrow x = 2,8\) Vậy \(x = 2,8\). Chọn C. Câu 25 (TH): Phương pháp: Áp dụng định nghĩa hai phân thức bằng nhau: \(\frac{A}{B} = \frac{C}{D}\) nếu \(A\,.\,D = B\,.\,C\) Cách giải: \(\begin{array}{l}\,\,\,\,\,\,\frac{{x - 2}}{{{x^2} + 4}} = \frac{{2{x^2} - 4x}}{P}\\ \Leftrightarrow \frac{{x - 2}}{{{x^2} + 4}} = \frac{{2x\left( {x - 2} \right)}}{P}\\ \Rightarrow P.\left( {x - 2} \right) = 2x\left( {x - 2} \right)\left( {{x^2} + 4} \right)\\ \Leftrightarrow P = 2x\left( {{x^2} + 4} \right)\\ \Leftrightarrow P = 2{x^3} + 8x\end{array}\) Vậy đa thức \(P\) trong đẳng thức \(\frac{{x - 2}}{{{x^2} + 4}} = \frac{{2{x^2} - 4x}}{P}\) là \(2{x^3} + 8x\). Chọn D. Câu 26 (VD): Phương pháp: + Tìm điều kiện xác định của phân thức. + Rút gọn phân thức + Thay giá trị của \(x\) (thỏa mãn điều kiện) để tính giá trị của của biểu thức. Cách giải: Điều kiện: \(x \ne 0;\,\,x \ne \frac{4}{3}\) \(\frac{{9{x^2} - 16}}{{3{x^2} - 4x}}\)\( = \frac{{{{\left( {3x} \right)}^2} - {4^2}}}{{x\left( {3x - 4} \right)}}\)\( = \frac{{\left( {3x - 4} \right)\left( {3x + 4} \right)}}{{x\left( {3x - 4} \right)}}\)\( = \frac{{3x + 4}}{x}\) Thay \(x = - 4\) \(\left( {tmdk} \right)\) vào biểu thức \(\frac{{3x + 4}}{x}\) ta được: \(\frac{{3.\left( { - 4} \right) + 4}}{{ - 4}}\)\( = \frac{{ - 12 + 4}}{{ - 4}}\)\( = \frac{{ - 8}}{{ - 4}} = 2\) Chọn B. Câu 27 (TH): Phương pháp: Trong \(\Delta ABC\) có \(AD\) là đường phân giác của góc \(BAC\). Áp dụng định lý đường phân giác trong tam giác ta có: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) Cách giải: Trong tam giác \(MNP\) có \(NQ\) là phân giác trong của góc \(MNP\). Áp dụng định lý đường phân giác trong tam giác nên ta có: \(\frac{{MN}}{{NP}} = \frac{{MQ}}{{PQ}}\) \( \Rightarrow PQ = \frac{{NP.MQ}}{{MN}} = \frac{{5.1,5}}{3} = 2,5\,\,\left( {cm} \right)\) Chọn A. Câu 28 (TH): Phương pháp: Muốn rút gọn một phân thức ta có thể: + Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung. + Chia cả tử và mẫu cho nhân tử chung. Cách giải: +) \(\frac{{{x^3}{y^3}}}{{x{y^4}}} = \frac{{{x^2}.x.{y^3}}}{{x.{y^3}.y}}\)\( = \frac{{{x^2}}}{y} \Rightarrow \) Đáp án A đúng. +) \(\frac{{{x^2} - {y^2}}}{{x - y}}\)\( = \frac{{\left( {x + y} \right)\left( {x - y} \right)}}{{x - y}}\) \( = x + y \Rightarrow \) Đáp án B đúng +) \(\frac{{{x^2} + {y^2}}}{{{y^2}}}\)\( = \frac{{{x^2}}}{{{y^2}}} + \frac{{{y^2}}}{{{y^2}}} = \frac{{{x^2}}}{{{y^2}}} + 1 \Rightarrow \) Đáp án C sai. +) \(\frac{{16{x^2}y\left( {y + x} \right)}}{{12xy\left( {x + y} \right)}}\) \( = \frac{{4x.4xy.\left( {x + y} \right)}}{{3.4xy.\left( {x + y} \right)}} = \frac{{4x}}{3} \Rightarrow \) Đáp án D đúng. Chọn C. Câu 29 (VDC): Phương pháp: Muốn rút gọn một phân thức ta có thể: + Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung. + Chia cả tử và mẫu cho nhân tử chung. Cách giải: \(\begin{array}{l}\,\,\,\,\,\,\frac{{{x^5} + {x^4} + 1}}{{{x^2} + x + 1}}\\ = \frac{{{x^5} - {x^3} + {x^2} + {x^4} - {x^2} + x + {x^3} - x + 1}}{{{x^2} + x + 1}}\\ = \frac{{{x^5} - {x^3} + {x^2} + {x^4} - {x^2} + x + {x^3} - x + 1}}{{{x^2} + x + 1}}\\ = \frac{{\left( {{x^5} - {x^3} + {x^2}} \right) + \left( {{x^4} - {x^2} + x} \right) + \left( {{x^3} - x + 1} \right)}}{{{x^2} + x + 1}}\\\, = \frac{{{x^2}\left( {{x^3} - x + 1} \right) + x\left( {{x^3} - x + 1} \right) + \left( {{x^3} - x + 1} \right)}}{{{x^2} + x + 1}}\\\, = \frac{{\left( {{x^2} + x + 1} \right)\left( {{x^3} - x + 1} \right)}}{{{x^2} + x + 1}}\\\, = {x^3} - x + 1\end{array}\) Vậy \(\frac{{{x^5} + {x^4} + 1}}{{{x^2} + x + 1}} = {x^3} - x + 1\). Chọn D. Câu 30 (VD): Phương pháp: Áp dụng định nghĩa tam giác đồng dạng: \(\Delta ABC \sim \Delta MNP\)\( \Rightarrow \left\{ \begin{array}{l}\angle A = \angle B = \angle C\\\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\end{array} \right.\) Cách giải: \(\Delta MNP \sim \Delta PQR\)\( \Rightarrow \frac{{MN}}{{PQ}} = \frac{{NP}}{{QR}} = \frac{{MP}}{{PR}}\) +) \(\frac{{MN}}{{PQ}} = \frac{{NP}}{{QR}}\)\( \Rightarrow MN.QR = NP.PQ\) +) \(\frac{{NP}}{{QR}} = \frac{{MP}}{{PR}}\)\( \Rightarrow MP.QR = NP.PR\) +) \(\frac{{MN}}{{PQ}} = \frac{{MP}}{{PR}}\)\( \Rightarrow MN.PR = MP.PQ\) Trong các đáp án trên, hệ thức không đúng là \(MN.PQ = NP.QR\). Chọn C.
|




















Danh sách bình luận