Đề số 22 - Đề kiểm tra học kì 1 - Toán 8

Đề bài

 a)\({x^2} + xy - x - y\)

Bài 4. Tính tổng \({x^4} + {y^4}\) biết \({x^2} + {y^2} = 18\) và \(xy = 5.\)

Bài 5. Cho tam giác ABC vuông tại A (AB < AC). M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.

a) Chứng minh tứ giác MDME là hình chữ nhật.

b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.

c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân.

d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.

LG bài 1

Lời giải chi tiết:

a)\({x^2} + xy - x - y = x\left( {x + y} \right) - \left( {x + y} \right) = \left( {x + y} \right)\left( {x - 1} \right).\)

b)\({a^2} - {b^2} + 8a + 16 = \left( {{a^2} + 8a + 16} \right) - {b^2} = {\left( {a + 4} \right)^2} - {b^2}\)

                                   \( = \left( {a + 4 - b} \right)\left( {a + 4 + b} \right).\)

LG bài 2

Lời giải chi tiết:

a) \(4x\left( {x + 1} \right) + \left( {3 - 2x} \right)\left( {3 + 2x} \right) = 15 \Rightarrow 4{x^2} + 4x + \left( {9 - 4{x^2}} \right) = 15\)

\( \Rightarrow 4{x^2} + 4x + 9 - 4{x^2} = 15 \Rightarrow 4x = 15 - 9 \Rightarrow 4x = 6 \Rightarrow x = {3 \over 2}.\)

b) \(3x\left( {x - 20012} \right) - x + 20012 = 0 \Rightarrow 3x\left( {x - 20012} \right) - \left( {x - 20012} \right) = 0\)

\( \Rightarrow \left( {x - 20012} \right)\left( {3x - 1} \right) = 0 \Rightarrow x - 20012 = 0\) hoặc \(3x - 1 = 0\)

\( \Rightarrow x = 20012\) hoặc \(x = {1 \over 3}.\)

LG bài 3

Lời giải chi tiết:

a) Điều kiện: \(x,y \ne 0;x \ne y.\)

\({1 \over {x\left( {x - y} \right)}} + {1 \over {y\left( {y - x} \right)}} = {1 \over {x\left( {x - y} \right)}} - {1 \over {y\left( {x - y} \right)}} = {{y - x} \over {xy\left( {x - y} \right)}} =  - {1 \over {xy}}.\)

b) Điều kiện: \(x \ne  \pm 1.\)

\({{x - 3} \over {x + 1}} - {{x + 2} \over {x - 1}} - {{8x} \over {1 - {x^2}}} = {{x - 3} \over {x + 1}} - {{x + 2} \over {x - 1}} + {{8x} \over {{x^2} - 1}}\)

\( = {{\left( {x - 3} \right)\left( {x - 1} \right) - \left( {x + 2} \right)\left( {x + 1} \right) + 8x} \over {{x^2} - 1}}\)

\( = {{{x^2} - x - 3x + 3 - \left( {{x^2} + x + 2x + 2} \right) + 8x} \over {{x^2} - 1}}\)

\( = {{{x^2} - x - 3x + 3 - {x^2} - x - 2x - 2 + 8x} \over {{x^2} - 1}} = {{x + 2} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = {1 \over {x - 1}}.\)

LG bài 4

Lời giải chi tiết:

Ta có \({x^4} + {y^4} = {\left( {{x^2} + {y^2}} \right)^2} - 2{x^2}{y^2} = {18^2} - {2.5^2} = 274.\)

LG bài 5

Lời giải chi tiết:

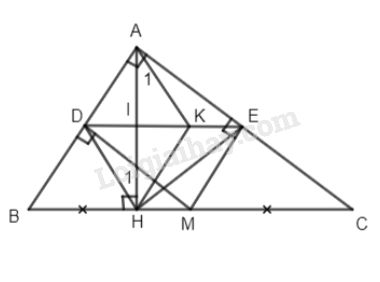
a) Ta có tứ giác ADME là hình chữ nhật (có ba góc vuông).

b) + Ta có \(ME\parallel AB\) (cùng vuông góc AC)

M là trung điểm của BC (gt)

\( \Rightarrow E\) là trung điểm của AC.

+ Ta có E là trung điểm của AC (cmt)

Chứng minh tương tự ta có D là trung điểm của AB

Do đó DE là đường trung bình của \(\Delta ABC\)

\( \Rightarrow DE\parallel BC\) và \(DE = {{BC} \over 2}\) hay \(DE\parallel MC\) và DE = MC

\( \Rightarrow \) Tứ giác CMDE là hình bình hành.

c) Ta có \(DE\parallel HM(cmt) \Rightarrow MHDE\) là hình thang    (1)

Lại có \(HE = {{AC} \over 2}\) (tính chất đường trung tuyến của tam giác vuông AHC)

\(DM = {{AC} \over 2}\) (DM là đường trung bình của \(\Delta ABC) \Rightarrow HE = DM\)    (2)

Từ (1) và (2) \( \Rightarrow MHDE\) là hình thang cân.

d)Gọi I là giao điểm của AH và DE. Xét \(\Delta AHB\) có D là trung điểm của AB, \(DI\parallel BH\left( {cmt} \right) \Rightarrow I\) là trung điểm của AH.

Xét \(\Delta DIH\) và \(\Delta KIA\) có IH = IA (cmt), \(\widehat {DIH} = \widehat {AIK}\) (đối đỉnh), \(\widehat {{H_1}} = \widehat {{A_1}}\) (so le trong)

\( \Rightarrow \Delta DIH = \Delta KIA(g.c.g) \Rightarrow ID = IK\)

Tứ giác ADHK có ID = IK, IA = IH (cmt) \) \Rightarrow DHK\) là hình bình hành

\( \Rightarrow HK\parallel DA\) mà \(DA \bot AC \Rightarrow HK \bot AC.\)

Loigiaihay.com