Đề số 16 - Đề kiểm tra học kì 1 - Toán 8

Đề bài

Bài 3 (2,5 điểm)Cho biểu thức: \(P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}\)

1. Rút gọn \(P\).
2. Tìm x để \(P = 0\)
3. Tính giá trị biểu thức \(P\) khi \(x\) thỏa mãn: \({x^2} - x = 0\).
4. Tìm giá trị lớn nhất của biểu thức \(Q = \dfrac{1}{{{x^2} - 9}}.P\)

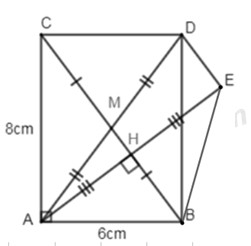
Bài 4 (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A,\,AB = 6\,cm,\,AC = 8\,cm\). Gọi \(M\) là trung điểm của đoạn \(BC\). Điểm \(D\) đối xứng với \(A\)  qua \(M\).

1. Chứng minh tứ giác \(AB{\rm{D}}C\) là hình chữ nhật. Tính diện tích hình chữ nhật \(AB{\rm{D}}C\).
2. Kẻ \(AH \bot BC\left( {H \in BC} \right)\), gọi \(E\) là điểm đối xứng với \(A\)  qua \(H\). Chứng minh: \(HM//DE\) và \(HM = \dfrac{1}{2}DE\).
3. Tính tỉ số \(\dfrac{{{S_{AHM}}}}{{{S_{A{\rm{ED}}}}}}\).
4. Chứng minh tứ giác \(BC{\rm{D}}E\) là hình thang cân.

LG bài 1

Lời giải chi tiết:

\(\begin{array}{l}1)\,\,2xy\left( {x + y} \right) = 2{x^2}y + 2x{y^2}\\2)\,\left( {x + 1} \right)\left( {2x - 1} \right) = 2{x^2} - x + 2x - 1 = 2{x^2} + x - 1\\3)\,\,10{{\rm{x}}^4}{y^3}:6{{\rm{x}}^2}{y^2} = \dfrac{{10}}{6}.{x^{4 - 2}}.{y^{3 - 2}} = \dfrac{5}{3}{x^2}y\\4)\;\;\left( {{x^3} - 8} \right):\left( {{x^2} + 2x + 4} \right) \\= \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right):\left( {{x^2} + 2x + 4} \right) \\= x - 2.\end{array}\)

LG bài 2

Lời giải chi tiết:

\(\begin{array}{l}1)\,\,2x{y^2} - 4y = 2y\left( {xy - 2} \right)\\2)\,\,{x^2}y - 6xy + 9y = y\left( {{x^2} - 6x + 9} \right) = y{\left( {x - 3} \right)^2}\\3)\,\,{x^2} + x - {y^2} + y = \left( {{x^2} - {y^2}} \right) + \left( {x + y} \right)\\ = \left( {x + y} \right)\left( {x - y} \right) + \left( {x + y} \right)\\ = \left( {x + y} \right)\left( {x - y + 1} \right)\\4)\,\,{x^2} + 4{\rm{x}} + 3 = {x^2} + 4{\rm{x}} + 4 - 1 \\= {\left( {x + 2} \right)^2} - 1\\ = \left( {x + 2 + 1} \right)\left( {x + 2 - 1} \right)\\ = \left( {x + 3} \right)\left( {x + 1} \right)\end{array}\)

LG bài 3

Lời giải chi tiết:

\(P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}\)

Điều kiện xác định: \(\left\{ \begin{array}{l}x \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne  - 1\end{array} \right.\)

\(\begin{array}{l}1)\,\,P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}} \\= \dfrac{{2{x^2} - 1}}{{x\left( {x + 1} \right)}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}\\ = \dfrac{{2{x^2} - 1 - \left( {x - 1} \right)\left( {x + 1} \right) + 3x}}{{x\left( {x + 1} \right)}}\\ = \dfrac{{2{x^2} - 1 - {x^2} + 1 + 3{\rm{x}}}}{{x\left( {x + 1} \right)}}\\ = \dfrac{{{x^2} + 3x}}{{x\left( {x + 1} \right)}}\\ = \dfrac{{x\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{x + 3}}{{x + 1}}.\end{array}\)

\(2)\,\,P = 0 \Leftrightarrow \dfrac{{x + 3}}{{x + 1}} = 0 \)

\(\Leftrightarrow x + 3 = 0 \Leftrightarrow x =  - 3\left( {tm} \right)\)

Vậy với \(x =  - 3\) thì \(P = 0.\)

\(3)\,\,{x^2} - x = 0 \Leftrightarrow x\left( {x - 1} \right) = 0\)

\(\Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \)

\(\Leftrightarrow \left[ \begin{array}{l}x = 0\;\;\left( {ktm} \right)\\x = 1\;\;\left( {tm} \right)\end{array} \right.\)

Thay \(x = 1\) vào biểu thức \(P\) ta được: \(\dfrac{{x + 3}}{{x + 1}} = \dfrac{{1 + 3}}{{1 + 1}} = 2\).

4) Ta có: \(Q = \dfrac{1}{{{x^2} - 9}}.P = \dfrac{1}{{{x^2} - 9}}.\dfrac{{x + 3}}{{x + 1}} \)

\(= \dfrac{{x + 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)\left( {x + 1} \right)}} \)

\(= \dfrac{1}{{\left( {x - 3} \right)\left( {x + 1} \right)}} = \dfrac{1}{{{x^2} - 2x - 3}}\)

\( \Rightarrow Q\) đạt giá trị lớn nhất \( \Leftrightarrow \left( {{x^2} - 2x - 3} \right)\) đạt giá trị nhỏ nhất.

Ta có: \({x^2} - 2x - 3 = {x^2} - 2x + 1 - 4 = {\left( {x - 1} \right)^2} - 4\).

Vì \({\left( {x - 1} \right)^2} \ge 0\,\,\forall x\)

\(\Rightarrow {\left( {x - 1} \right)^2} - 4 \ge  - 4\,\,\forall x \)

\(\Rightarrow \dfrac{1}{{{x^2} - 2x - 3}} \le  - \dfrac{1}{4}\)

\( \Rightarrow Q\;\;\max  =  - \dfrac{1}{4} \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\;\;\left( {tm} \right).\)

Vậy \(Max\;Q =  - \dfrac{1}{4}\;\;khi\;\;x = 1.\)

LG bài 4

Lời giải chi tiết:

1.Xét tứ giác \(AB{\rm{D}}C\) có \(A{\rm{D}}\) và \(BC\) cắt nhau tại trung điểm \(M\) của mỗi đường (gt)

\( \Rightarrow AB{\rm{D}}C\) là hình bình hành (dhnb)

Lại có \(\angle BAC = {90^0}\left( {gt} \right) \Rightarrow \) hình bình hành \(AB{\rm{D}}C\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

Ta có: \({S_{AB{\rm{D}}C}} = AB.AC = 6.8 = 48\,c{m^2}\)

2.Xét \(\Delta A{\rm{D}}E\) có \(H,\,M\)là trung điểm của \(A{\rm{E}}\) và \(A{\rm{D}}\) (gt)

\( \Rightarrow HM\) là đường trung bình của \(\Delta A{\rm{D}}E\) (dhnb)

\( \Rightarrow \left\{ \begin{array}{l}HM = \dfrac{1}{2}DE\\HM//DE\end{array} \right.\) (tính chất)

3.Xét \(\Delta A{\rm{D}}E\) có: \(MH//DE\left( {cmt} \right) \Rightarrow \dfrac{{AM}}{{A{\rm{D}}}} = \dfrac{{AH}}{{A{\rm{E}}}} = \dfrac{{MH}}{{DE}}\) (định lý Ta-lét)

\(\Delta AHM \sim \Delta A{\rm{ED}}\left( {c - c - c} \right) \)

\(\Rightarrow \dfrac{{{S_{AHM}}}}{{{S_{A{\rm{ED}}}}}} = {\left( {\dfrac{{HM}}{{DE}}} \right)^2} = \dfrac{1}{4}\;\;\;\left( {dpcm} \right).\)

4.Ta có: \(MH//DE\left( {cmt} \right) \Rightarrow BC//DE \Rightarrow BC{\rm{D}}E\) là hình thang (dhnb)

Xét \(\Delta ABE\) có: \(BH\) vừa là trung tuyến vừa là đường cao nên \(\Delta ABE\)là tam giác cân tại B (dhnb)

\( \Rightarrow BH\) là phân giác của \(\angle ABE\) (tính chất)

\( \Rightarrow \angle ABC = \angle CBE\) (tính chất tia phân giác)

Mà \(\angle ABC = \angle BC{\rm{D}}\) (so le trong)

\( \Rightarrow \angle CBE = \angle BC{\rm{D}}\)\( \Rightarrow \) hình thang \(BC{\rm{D}}E\) là hình thang cân (dhnb). 

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại Tuyensinh247.com

 Loigiaihay.com