Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GD&ĐT Lập Thạch

I. PHẦN TRẮC NGHIỆM (3,0 điểm).

Viết phương án đúng (A, B, C hoặc D) vào bài thi.

Câu 1. Khai triển hằng đẳng thức \({\left( {x - y} \right)^2}\) được kết quả là

A. \({x^2} + xy + {y^2}\)

B. \({x^2} - xy + {y^2}\)

C. \({x^2} + 2xy + {y^2}\)

D. \({x^2} - 2xy + {y^2}\)

Câu 2. Cho \(\dfrac{A}{{x - 1}} = \dfrac{x}{{1 - x}}\). Khi đó \(A\) bằng

A. \(x\)                                  B. \(1 - x\)

C. \(x - 1\)                 D. \( - x\)

Câu 3. Kết quả của phép chia \(\left( {2{x^2} + x} \right):x\) là

A. \(2x\)                    B. \(2x + 1\)

C. \(2\)                                   D. \(2{x^2} + 1\)

Câu 4. Rút gọn phân thức \(\dfrac{{2x - 2y}}{{x - y}}\) ta được kết quả là

A. \(x - y\)    B. \(2x\)

C. \(2\)                       D. \(2\left( {x - y} \right)\)

Câu 5. Cho hình bình hành \(ABCD\). Khi đó

A. \(AC = BD\)

B. \(AB = AD\)

C. \(AB = CD\)

D. \(AC \bot BD\)

Câu 6. Một thửa ruộng hình chữ nhật có chiều dài \(20m\), chiều rộng \(5m\). Diện tích thửa ruộng bằng

A. \(100{m^2}\)                  B. \(25{m^2}\)

C. \(50{m^2}\)                    D. \(4{m^2}\)

II. PHẦN TỰ LUẬN (7,0 điểm).

Câu 7. (1,0 điểm) Phân tích đa thức thành nhân tử:

a) \(x\left( {y - 1} \right) - 3\left( {y - 1} \right)\)

b) \(4{x^2} - {y^2} + 8\left( {y - 2} \right)\)

Câu 8. (1,5 điểm) Rút gọn biểu thức 

a) \({\left( {x + y} \right)^2} - {x^2} - {y^2}\)

b) \(A = \dfrac{1}{{x + 1}} + \dfrac{1}{{{x^2} + x}}\) với \(x \ne 0,x \ne  - 1\).

Câu 9. (1,0 điểm) Tìm \(x\) biết:

a) \(3x\left( {x + 2} \right) - x\left( {3x + 5} \right) = 5\)

b) \({x^2} - 4 = 0\)

Câu 10. (2,5 điểm) Cho tam giác \(ABC\) vuông tại \(A,\) \(M\) là trung điểm của \(BC\). Đường thẳng qua \(M\) song song với \(AB\) cắt \(AC\) tại \(D\), đường thẳng qua \(M\) song song với \(AC\) cắt \(AB\) tại \(E\).

a) Chứng minh rằng tứ giác \(ADME\) là hình chữ nhật.

b) Nếu \(AB = AC\) thì tứ giác \(ADME,BEDC\) là hình gì? Vì sao?

Câu 11. (1,0 điểm) Chứng minh rằng với mọi số nguyên \(m,n\) ta đều có \({m^3}n - m{n^3}\) chia hết cho \(6\).

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM (23 điểm)

Câu 1 (NB):

Phương pháp:

Sử dụng hằng thức số hai: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\).

Cách giải:

Ta có: \({\left( {x - y} \right)^2} = {x^2} - 2xy + {y^2}\).

Chọn D.

Câu 2 (TH):

Phương pháp:

Biến đổi về hai phân thức cùng mẫu, cho tử bằng nhau.

Cách giải:

Ta có:

\(\begin{array}{l}\dfrac{A}{{x - 1}} = \dfrac{x}{{1 - x}}\\ \Rightarrow \dfrac{A}{{x - 1}} = \dfrac{{ - x}}{{x - 1}}\\ \Rightarrow A =  - x\end{array}\)

Chọn D.

Câu 3 (NB):

Phương pháp:

Chia đa thức cho đơn thức: Ta chia từng đơn thức trong đa thức cho đơn thức và cộng các kết quả lại với nhau.

Cách giải:

\(\left( {2{x^2} + x} \right):x\)\( = 2{x^2}:x + x:x = 2x + 1\).

Chọn B.

Câu 4 (TH):

Phương pháp:

Rút gọn phân thức: Chia cả tử và mẫu của phân thức cho nhân tử chung của tử và mẫu.

Cách giải:

\(\dfrac{{2x - 2y}}{{x - y}} = \dfrac{{2\left( {x - y} \right)}}{{x - y}} = 2\).

Chọn C.

Câu 5 (NB):

Phương pháp:

Sử dụng tính chất hình bình hành:

- Hai cạnh đối song song và bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm mỗi đường.

Cách giải:

\(ABCD\) là hình bình hành thì \(AB = CD\).

Chọn C.

Câu 6 (TH):

Phương pháp:

Diện tích hình chữ nhật: \(S = ab\).

Cách giải:

Diện tích thửa ruộng là: \(S = 20.5 = 100\left( {{m^2}} \right)\).

Chọn A.

PHẦN II. TỰ LUẬN (7,0 điểm).

Câu 7 (TH):

Phương pháp:

Phân tích đa thức bằng cách nhóm các hạng tử thích hợp rồi đặt nhân tử chung, kết hợp dùng hằng đẳng thức.

Cách giải:

a) \(x\left( {y - 1} \right) - 3\left( {y - 1} \right)\)\( = \left( {y - 1} \right)\left( {x - 3} \right)\).

b) \(4{x^2} - {y^2} + 8\left( {y - 2} \right)\)

\(\begin{array}{l} = 4{x^2} - {y^2} + 8y - 16\\ = 4{x^2} - \left( {{y^2} - 8y + 16} \right)\\ = {\left( {2x} \right)^2} - {\left( {y - 4} \right)^2}\\ = \left( {2x - y + 4} \right)\left( {2x + y - 4} \right)\end{array}\)  

Câu 8 (VD):

Phương pháp:

a) Khai triển hằng đẳng thức và rút gọn.

b) Qui đồng mẫu thức và rút gọn phân thức.

Cách giải:

a) \({\left( {x + y} \right)^2} - {x^2} - {y^2}\)

\(\begin{array}{l} = {x^2} + 2xy + {y^2} - {x^2} - {y^2}\\ = \left( {{x^2} - {x^2}} \right) + \left( {{y^2} - {y^2}} \right) + 2xy\\ = 0 + 0 + 2xy\\ = 2xy\end{array}\)

b) \(A = \dfrac{1}{{x + 1}} + \dfrac{1}{{{x^2} + x}}\) với \(x \ne 0,x \ne  - 1\).

\(\begin{array}{l}A = \dfrac{1}{{x + 1}} + \dfrac{1}{{x\left( {x + 1} \right)}}\\A = \dfrac{x}{{x\left( {x + 1} \right)}} + \dfrac{1}{{x\left( {x + 1} \right)}}\\A = \dfrac{{x + 1}}{{x\left( {x + 1} \right)}} = \dfrac{1}{x}\end{array}\)

Vậy \(A = \dfrac{1}{x}\).

Câu 9 (VD):

Phương pháp:

a) Rút gọn vế trái, sử dụng qui tắc chuyển vế tìm \(x\).

b) Phân tích đa thức thành nhân tử và sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).

Cách giải:

a) \(3x\left( {x + 2} \right) - x\left( {3x + 5} \right) = 5\)

\(\begin{array}{l}3{x^2} + 6x - \left( {3{x^2} + 5x} \right) = 5\\3{x^2} + 6x - 3{x^2} - 5x = 5\\x = 5\end{array}\)

Vậy \(x = 5\).

b) \({x^2} - 4 = 0\)

\(\left( {x - 2} \right)\left( {x + 2} \right) = 0\)

TH1: \(x - 2 = 0\)

\(\begin{array}{l}x = 0 + 2\\x = 2\end{array}\)

TH2: \(x + 2 = 0\)

\(\begin{array}{l}x = 0 - 2\\x =  - 2\end{array}\)

Vậy \(x = 2\) hoặc \(x =  - 2\).

Câu 10 (VD):

Phương pháp:

a) Sử dụng dấu hiệu nhận biết: Tứ giác có ba góc vuông là hình chữ nhật.

b) Sử dụng dấu hiệu nhận biết hình vuông: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Cách giải:

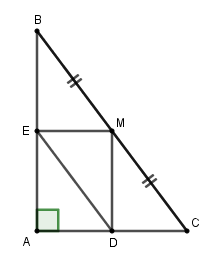
a) Chứng minh rằng tứ giác \(ADME\) là hình chữ nhật.

Ta có: \(\left\{ \begin{array}{l}ME//AC\\AB \bot AC\end{array} \right. \Rightarrow ME \bot AB\) (từ vuông góc đến song song)

\( \Rightarrow \widehat {MEA} = {90^0}\)

Lại có: \(\left\{ \begin{array}{l}MD//AB\\AB \bot AC\end{array} \right. \Rightarrow MD \bot AC\) (từ vuông góc đến song song)

\( \Rightarrow \widehat {MDA} = {90^0}\).

Tứ giác \(ADME\) có: \(\widehat A = {90^0}\left( {gt} \right)\), \(\widehat {MEA} = \widehat {MDA} = {90^0}\left( {cmt} \right)\) nên là hình chữ nhật (dhnb).

Vậy tứ giác \(ADME\) là hình chữ nhật.

b) Nếu \(AB = AC\) thì tứ giác \(ADME,BEDC\) là hình gì? Vì sao?

Tam giác \(ABC\) có \(M\) là trung điểm \(BC\) và \(ME//AC\) nên \(E\) là trung điểm của \(AB\).

\( \Rightarrow ME\) là đường trung bình của \(\Delta ABC\) \( \Rightarrow ME = \dfrac{1}{2}AC\) (tính chất)  (1)

Lại có: \(M\) là trung điểm \(BC\) và \(MD//AB\) nên \(D\) là trung điểm của \(AC\).

\( \Rightarrow MD\) là đường trung bình của \(\Delta ABC\) \( \Rightarrow MD = \dfrac{1}{2}AB\) (tính chất)  (2)

Mà \(AB = AC\left( {gt} \right)\) nên từ (1) và (2) suy ra \(ME = MD\).

Hình chữ nhật \(ADME\) có \(ME = MD\) nên là hình vuông (hình chữ nhật có hai cạnh kề bằng nhau là hình vuông).

Ta có: \(D,E\) là trung điểm của \(AC,AB\) nên \(DE\) là đường trung bình của \(\Delta ABC\) \( \Rightarrow DE//BC\) nên tứ giác \(DEBC\) là hình thang.

Mà \(AB = AC \Rightarrow \Delta ABC\) cân tại \(A\) \( \Rightarrow \widehat B = \widehat C\).

Hình thang \(DEBC\) có \(\widehat B = \widehat C\) nên là hình thang cân (hình thang có hai góc kề một đáy bằng nhau là hình thang cân).

Vậy \(ADME\) là hình vuông, \(DEBC\) là hình thang cân.

Câu 11 (VDC):

Phương pháp:

- Đặt \(A = {m^3}n - m{n^3}\).

- Đưa \(A\) về dạng tích, chứng minh \(A \vdots 3\) và \(A \vdots 2\) suy ra điều phải chứng minh.

Cách giải:

Đặt \(A = {m^3}n - m{n^3}\)\( = mn\left( {{m^2} - {n^2}} \right)\)\( = mn\left( {m - n} \right)\left( {m + n} \right)\)

+) Chứng minh \(A \vdots 3\).

- Nếu \(m = 3k\) hoặc \(n = 3k\) thì \(A \vdots 3\)

- Nếu \(m = 3k + 1,n = 3l + 1\) thì:

\(m - n = 3k + 1 - 3l - 1\) \( = 3\left( {k - l} \right) \vdots 3\) \( \Rightarrow A \vdots 3\)

- Nếu \(m = 3k + 1,n = 3l + 2\) thì:

\(m + n = 3k + 1 + 3l + 2\) \( = 3\left( {k + l + 1} \right) \vdots 3\) \( \Rightarrow A \vdots 3\)

- Nếu \(m = 3k + 2,n = 3l + 1\) thì:

\(m + n = 3k + 2 + 3l + 1\) \( = 3\left( {k + l + 1} \right) \vdots 3\) \( \Rightarrow A \vdots 3\)

- Nếu \(m = 3k + 2,n = 3l + 2\) thì:

\(m - n = 3k + 2 - 3l - 2\) \( = 3\left( {k - l} \right) \vdots 3\) \( \Rightarrow A \vdots 3\)

Do đó với mọi \(m,n \in \mathbb{Z}\) thì \(A \vdots 3\)  (1)

+) Chứng minh \(A \vdots 2\).

Nếu \(m = 2k\) hoặc \(n = 2k\) thì \(A \vdots 2\).

Nếu \(m = 2k + 1,n = 2l + 1\) thì \(m + n = 2k + 1 + 2l + 1\) \( = 2k + 2l + 2 = 2\left( {k + l + 1} \right) \vdots 2\)

\( \Rightarrow A = mn\left( {m - n} \right)\left( {m + n} \right) \vdots 2\).

Do đó với mọi \(m,n \in \mathbb{Z}\) thì \(A \vdots 2\) (2)

Từ (1) và (2) suy ra \(A \vdots 6\) (do \(\left( {2;3} \right) = 1\)). (đpcm)

HẾT

Loigiaihay.com