Đề kiểm tra giữa kì 1 Toán 8 - Đề số 5 có lời giải chi tiếtĐề kiểm tra giữa kì I Toán 8 - Đề số 5 có lời giải chi tiết Quảng cáo
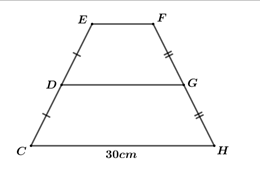
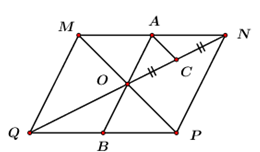
Đề bài Câu 1 (2 điểm): Thực hiện các phép tính: a) \( - 7{x^2}\left( {3x - 4y} \right)\) b) \(\left( {x - 3} \right)\left( {5x - 4} \right)\) c) \({\left( {2x - 1} \right)^2}\) d) \(\left( {x + 3} \right)\left( {x - 3} \right)\) Câu 2 (3 điểm): Phân tích đa thức thành nhân tử: a) \(2{x^3} - 3{x^2}\) b) \({x^2} + 5xy + x + 5y\) c) \({x^2} - 36 + 4xy + 4{y^2}\) Câu 3 (0,5 điểm): Tìm \(x\), biết: \({x^2} - 5x + 6 = 0\) Câu 4 (1 điểm): Một người thợ làm bánh thiết kế một chiếc bánh cưới có \(3\) tầng hình tròn như hình bên. Tầng đáy có đường kính \(CH\) là \(30cm\). Tầng thứ \(2\) có đường kính \(DG\) nhỏ hơn đường kính tầng đáy \(10cm\). Em hãy tính độ dài đường kính \(EF\) của tầng \(1\), nếu biết rằng \(EF\,{\rm{//}}\,CH\) và \(D,\,\,G\) lần lượt là trung điểm của \(EC\) và \(FH\)? Câu 5 (1 điểm): Có \(10\) túi đựng tiền vàng hình dạng giống hệt nhau. Trong đó, có một túi đựng tiền giả. Những đồng tiền giả nhẹ hơn một gam so với đồng tiền thật nặng \(10\) gam. Bằng một chiếc cân đồng hồ và với chỉ một lần cân, hãy tìm ra túi đựng tiền giả? Câu 6 (2,5 điểm): Một hình bình hành \(MNPQ\) có \(2\) đường chéo cắt nhau tại \(O\). Qua \(O\) vẽ đường thẳng song song với \(NP\) lần lượt cắt \(MN\) và \(PQ\) tại \(A\) và \(B\). a) Chứng minh rằng \(ANPB\) là hình bình hành. b) Chứng minh rằng \(A\) là trung điểm của \(MN\). c) Gọi \(C\) là trung điểm của \(ON\). Chứng minh \(MP = 4AC\).
Lời giải chi tiết Câu 1: Phương pháp: a) Áp dụng quy tắc nhân đơn thức với đa thức. b) Áp dụng quy tắc nhân đa thức với đa thức. c) Khai triển hằng đẳng thức bình phương của một hiệu. d) Áp dụng hằng đẳng thức hiệu hai bình phương. Cách giải:
Câu 2: Phương pháp: a) Áp dụng phương pháp đặt nhân tử chung. b) Áp dụng phương pháp nhóm và đặt nhân tử chung. c) Áp dụng phương pháp nhóm và dùng hằng đẳng thức. Cách giải:
Câu 3:
Phương pháp: Phân tích đa thức \({x^2} - 5x + 6\) thành nhân tử bằng phương pháp tách. Cách giải: Tìm \(x\), biết: \({x^2} - 5x + 6 = 0\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\,{x^2} - 5x + 6 = 0\\ \Leftrightarrow {x^2} - 2x - 3x + 6 = 0\\ \Leftrightarrow \left( {{x^2} - 2x} \right) - \left( {3x - 6} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\end{array} \right..\end{array}\) Vậy \(x \in \left\{ {2;\,\,3} \right\}\). Câu 4: Phương pháp: Áp dụng định lý đường trung bình của hình thang. Cách giải: Câu 1: Phương pháp: a) Áp dụng quy tắc nhân đơn thức với đa thức. b) Áp dụng quy tắc nhân đa thức với đa thức. c) Khai triển hằng đẳng thức bình phương của một hiệu. d) Áp dụng hằng đẳng thức hiệu hai bình phương. Cách giải:
Câu 2: Phương pháp: a) Áp dụng phương pháp đặt nhân tử chung. b) Áp dụng phương pháp nhóm và đặt nhân tử chung. c) Áp dụng phương pháp nhóm và dùng hằng đẳng thức. Cách giải:
Câu 3 (VD) Phương pháp: Phân tích đa thức \({x^2} - 5x + 6\) thành nhân tử bằng phương pháp tách. Cách giải: Tìm \(x\), biết: \({x^2} - 5x + 6 = 0\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\,{x^2} - 5x + 6 = 0\\ \Leftrightarrow {x^2} - 2x - 3x + 6 = 0\\ \Leftrightarrow \left( {{x^2} - 2x} \right) - \left( {3x - 6} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\end{array} \right..\end{array}\) Vậy \(x \in \left\{ {2;\,\,3} \right\}\). Câu 4: Phương pháp: Áp dụng định lý đường trung bình của hình thang. Cách giải: Ta có: \(DG = CH - 10cm = 30cm - 10cm = 20cm\) Vì \(EF\,{\rm{//}}\,DH\) nên tứ giác \(EFHC\) là hình thang. (định nghĩa) Xét hình thang \(EFHC\) ta có: \(D,\,\,G\) lần lượt là trung điểm của \(EC\) và \(FH\) \( \Rightarrow DG\) là đường trung bình của hình thang \(EFHC\) (định nghĩa) \( \Rightarrow DG = \frac{1}{2}\left( {EF + CH} \right)\) (tính chất đường trung bình) \(\begin{array}{l} \Leftrightarrow 2DG = EF + CH\\ \Leftrightarrow EF = 2DG - CH\\ \Leftrightarrow EF = 2.20 - 30 = 10\,\,cm.\end{array}\) Vậy \(EF = 10cm\). Câu 5: Phương pháp: Đánh số 10 ví theo thứ tự từ 1 đến 10. Lấy trong các ví số đồng tiền theo thứ tự đánh số tương ứng. Áp dụng phương pháp giả thiết tạm. Cách giải: Đánh số \(10\) túi theo thứ tự \(1,\,\,2,\,\,3, \ldots ,\,\,10\). Lấy từ túi \(1\) ra \(1\) đồng Lấy từ túi \(2\) ra \(2\) đồng … Lấy từ túi \(10\) ra \(10\) đồng \( \Rightarrow \) Ta lấy được tất cả \(1 + 2 + ... + 10 = \frac{{10\left( {10 + 1} \right)}}{2} = 55\) đồng. Khi đó, \(55\) đồng này sẽ cân nặng \(a\) gam \(\left( {a > 0} \right).\) Giả sử \(55\) đồng này đều là tiền thật thì chúng có cân nặng là: \(10.55 = 550\)(gam) Mà tiền giả nhẹ hơn một gam so với tiền thật nên \(a < 550\). Sau khi cân, thực hiện phép tính \(550 - a\). Nếu \(550 - a = 9\) thì túi \(1\) là túi đựng tiền giả. Nếu \(550 - a = 9.2\) thì túi \(2\) là túi đựng tiền giả. …. Như vậy chỉ sau một lần cân ta có thể tìm được túi tiền đựng tiền giả. Câu 6: Phương pháp: a) Áp dụng dấu hiệu nhận biết hình bình hành. b) Áp dụng định lí đường trung bình của tam giác. c) Áp dụng tính chất hình bình hành và định lý đường trung bình của tam giác. Cách giải: a) Chứng minh rằng \(ANPB\) là hình bình hành. Vì \(MNPQ\) là hình bình hành nên \(MN\,{\rm{//}}\,PQ\) (tính chất hình bình hành) \( \Rightarrow AN\,{\rm{//}}\,BP\) Theo đề bài, ta có: \(AB\,{\rm{//}}\,NP\) \( \Rightarrow \) Tứ giác \(ANPB\) là hình bình hành (dhnb). b) Chứng minh rằng \(A\) là trung điểm của \(MN\). Ta có: \(MNPQ\) là hình bình hành có \(O\) là giao điểm hai đường chéo \( \Rightarrow \) \(O\) là trung điểm của \(MP\) (tính chất hình bình hành). Xét \(\Delta MNP\) ta có: \(OA\,{\rm{//}}\,NP\) Mà \(O\) là trung điểm của \(MP\) (cmt) \( \Rightarrow A\) là trung điểm của \(MN\) (định lý đảo). c) Gọi \(C\) là trung điểm của \(ON\). Chứng minh \(MP = 4AC\). Xét \(\Delta MON\) ta có: \(A\) là trung điểm của \(MN\) \(C\) là trung điểm của \(ON\) \( \Rightarrow \) \(OA\) là đường trung bình của \(\Delta MNP\) (định nghĩa đường trung bình) \( \Rightarrow AC = \frac{1}{2}OM\) (tính chất đường trung bình) Ta lại có: \(OM = \frac{1}{2}MP\) (cmt) \( \Rightarrow AC = \frac{1}{4}MP \Rightarrow MP = 4AC\,\,\,\left( {dpcm} \right).\)
|





















Danh sách bình luận