Đề kiểm tra 15 phút chương 6: Đa giác, diện tích đa giác - Đề số 1Đề bài
Câu 1 :
Mỗi góc trong của đa giác đều $n$ cạnh là:
Câu 2 :
Hình chữ nhật có chiều dài tăng $4$ lần, chiều rộng giảm $2$ lần, khi đó diện tích hình chữ nhật
Câu 3 :
Cho tam giác \(ABC\), đường cao \(AH = 9\,cm\), cạnh \(BC = 12\,cm\). Diện tích tam giác là:
Câu 4 :
Tam giác $ABC$ vuông tại $A$ , vẽ hình chữ nhật $ABDC$ . Biết diện tích của tam giác vuông là \(140\,c{m^2}\). Diện tích hình chữ nhật $ABDC$ là:
Cho tam giác $ABC$ có diện tích \(12\,c{m^2}\) . Gọi $N$ là trung điểm của$BC$ , $M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ . Câu 5
Khẳng định nào sau đây là đúng nhất?
Câu 6
Tính diện tích tam giác AOM
Câu 7 :
Chọn câu đúng.
Câu 8 :
Số đo mỗi góc trong và ngoài của đa giác đều \(8\) cạnh lần lượt là:
Câu 9 :
Đa giác nào dưới đây có số đường chéo bằng số cạnh?
Câu 10 :
Cho hình chữ nhật \(ABCD\) có \(AC\) là đường chéo. Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Mỗi góc trong của đa giác đều $n$ cạnh là:
Đáp án : D Phương pháp giải :
Mỗi góc của đa giác đều $n$ cạnh bằng \(\dfrac{{\left( {n - 2} \right).180^\circ }}{n}\). Lời giải chi tiết :
Mỗi góc của đa giác đều $n$ cạnh bằng \(\dfrac{{\left( {n - 2} \right).180^\circ }}{n}\).
Câu 2 :
Hình chữ nhật có chiều dài tăng $4$ lần, chiều rộng giảm $2$ lần, khi đó diện tích hình chữ nhật
Đáp án : B Phương pháp giải :
Sử dụng công thức tính diện tích hình chữ nhật bằng tích chiều dài nhân chiều rộng. Lời giải chi tiết :
Theo công thức tính diện tích hình chữ nhật \(S = a.b\) thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó Nếu \(a' = 4a;\,\,\,b' = \dfrac{1}{2}b;\,\) thì \(S' = a'.b' = 4a.\dfrac{1}{2}b = \dfrac{4}{2}ab = \dfrac{4}{2}S = 2S.\) Do đó diện tích tăng \(2\) lần so với diện tích đã cho.
Câu 3 :
Cho tam giác \(ABC\), đường cao \(AH = 9\,cm\), cạnh \(BC = 12\,cm\). Diện tích tam giác là:
Đáp án : C Phương pháp giải :
Sử dụng công thức: Diện tích tam giác bằng nửa tích một cạnh với chiều cao ứng với cạnh đó: \(S = \dfrac{1}{2}ah\) . Lời giải chi tiết :
Từ công thức tính diện tích tam giác ta có \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.9.12 = 54\,c{m^2}\) . Chú ý
Một số em quên hệ số \(\dfrac{1}{2}\) ở công thức diện tích dẫn đến ra A sai.
Câu 4 :
Tam giác $ABC$ vuông tại $A$ , vẽ hình chữ nhật $ABDC$ . Biết diện tích của tam giác vuông là \(140\,c{m^2}\). Diện tích hình chữ nhật $ABDC$ là:
Đáp án : B Phương pháp giải :
Dựa vào công thức tính diện tích hình chữ nhật và tam giác vuông để suy ra mối liên hệ \({S_{ABDC}} = 2{S_{ABC}}\) . Từ đó tính ra được diện tích \(ABDC\) . Lời giải chi tiết :
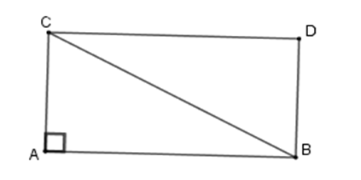 Vì \(ABDC\) là hình chữ nhật nên \({S_{ABDC}} = AC.AB\) mà \({S_{ABC}} = \dfrac{{AC.AB}}{2}\) Nên \({S_{ABDC}} = 2{S_{ABC}} = 2.140 = 280\,c{m^2}\) . Cho tam giác $ABC$ có diện tích \(12\,c{m^2}\) . Gọi $N$ là trung điểm của$BC$ , $M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ . Câu 5
Khẳng định nào sau đây là đúng nhất?
Đáp án : D Phương pháp giải :
Sử dụng tính chất của đường trung bình trong tam giác để so sánh các đoạn thẳng. Lời giải chi tiết :
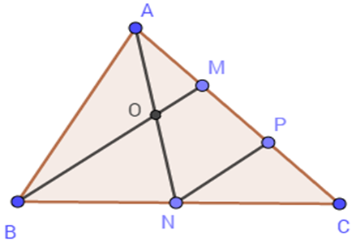 + Lấy $P$ là trung điểm của$CM$ . Tam giác BCM có: \(\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.\) Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa). Suy ra \(NP{\rm{//}}BM\) (tính chất đường trung bình). Tam giác $ANP$ có \(\left\{ \begin{array}{l}MA = MP\,\,\,(gt)\\OM{\rm{//}}NP\,\,\,({\rm{do}}\,\,NP{\rm{//}}BM)\end{array} \right.\) \( \Rightarrow AO = ON\) (định lý đảo của đường trung bình) . + Ta có $OM$ là đường trung bình của tam giác $ANP$ (cmt) nên \(OM = \dfrac{1}{2}NP\,\,\,\,(1)\) $NP$ là đường trung bình của tam giác $BCM$ nên \(NP = \dfrac{1}{2}BM\,\,\,(2)\) Từ (1) và (2) suy ra \(BM = 4OM \Rightarrow BO = 3OM\) . Vậy \(AO = ON;\,BO = 3OM\) . Câu 6
Tính diện tích tam giác AOM
Đáp án : B Phương pháp giải :
Sử dụng tỉ lệ của diện tích các tam giác. Lời giải chi tiết :
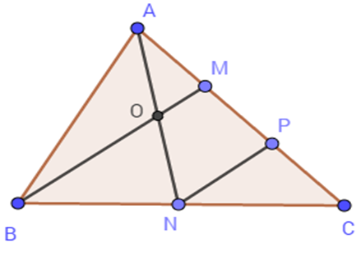 Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}} = \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}\) Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên \(\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3} \Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}\) Vậy \({S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)\)
Câu 7 :
Chọn câu đúng.
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa đa giác đều: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Lời giải chi tiết :
Hình chữ nhật là đa giác không đều vì hình chữ nhật có \(4\) góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều. Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.
Câu 8 :
Số đo mỗi góc trong và ngoài của đa giác đều \(8\) cạnh lần lượt là:
Đáp án : C Phương pháp giải :
Số đo góc của hình n giác đều: \(\dfrac{{\left( {n - 2} \right){{. 180}^0}}}{n}\) (với \(n \ge 3\)). Góc trong và góc ngoài n giác đều kề bù. Lời giải chi tiết :
Số đo góc trong của hình đa giác đều \(7\) cạnh là: \(\dfrac{{\left( {8 - 2} \right){{. 180}^0}}}{8} = 135^\circ \). Vì góc trong và ngóc ngoài đa giác kề bù nên số đo góc ngoài ngũ giác đều là: \(180^\circ - 135^\circ = 45^\circ \).
Câu 9 :
Đa giác nào dưới đây có số đường chéo bằng số cạnh?
Đáp án : B Phương pháp giải :
Số đường chéo của đa giác \(n\left( {n \ge 3} \right)\) cạnh là \(\dfrac{{n\left( {n - 3} \right)}}{2}\). Lời giải chi tiết :
Gọi số cạnh của đa giác là \(n\left( {n \ge 3;\,n \in \mathbb{N}} \right)\) Số đường chéo của đa giác là \(\dfrac{{n\left( {n - 3} \right)}}{2}\) Theo đề bài ta có: \(\dfrac{{n\left( {n - 3} \right)}}{2} = n \Leftrightarrow {n^2} - 3n = 2n\)\( \Leftrightarrow {n^2} - 5n = 0 \Leftrightarrow n\left( {n - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}n = 0\left( {ktm} \right)\\n = 5\left( {tm} \right)\end{array} \right.\) Vậy đa giác thỏa mãn đề bài là ngũ giác.
Câu 10 :
Cho hình chữ nhật \(ABCD\) có \(AC\) là đường chéo. Chọn câu đúng.
Đáp án : B Phương pháp giải :
+ Diện tích hình chữ nhật bằng tích hai kích thước của nó: \(S = a.b\). + Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông. Lời giải chi tiết :
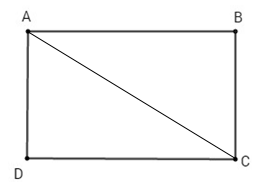 Vì \(ABCD\) là hình chữ nhật nên \({S_{ABCD}} = AD.DC = AB.AD\) nên A sai, B đúng Ta có: \(\Delta ADC,\,\Delta ABC\) là các tam giác vuông nên \({S_{ADC}} = \dfrac{1}{2}AD.DC;\,{S_{ABC}} = \dfrac{1}{2}AB.BC\), do đó C, D sai. |



















Danh sách bình luận