Trắc nghiệm Tổng hợp bài tập định luật Ôm - Vật Lí 11Đề bài
Câu 1 :
Cho mạch điện như hình vẽ: \({E_1} = 8V\), \({r_1} = 1,2\Omega \), \({E_2} = 4V\), \({r_2} = 0,4\Omega \), \(R = 28,4\Omega \), \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch và chiều của nó là? 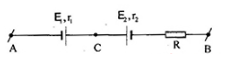
Câu 2 :
Cho mạch điện như hình vẽ: 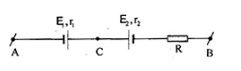 \({E_1} = 8V,{r_1} = 1,2\Omega \), \({E_2} = 4V,{r_2} = 0,4\Omega \), \(R = 28,4\Omega\), \({U_{AB}} = 6V\). Hiệu điện thế \({U_{AC}}\) và \({U_{CB}}\) là:
Câu 3 :
Cho mạch điện như hình vẽ: E1 = 2,1V, E2 = 1,5V, r1 = r2 = 0, R1 = R3 = 10$\Omega $; R2 = 20$\Omega $ Cường độ dòng điện qua R3 là: 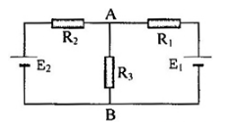
Câu 4 :
Cho mạch điện như hình vẽ: R = 10$\Omega $, r1 = r2 = 1$\Omega $, RA = 0. Khi dịch chuyển con chạy đến giá trị R0 số chỉ của ampe kế không đổi bằng 1A. Xác định E1; E2 ? 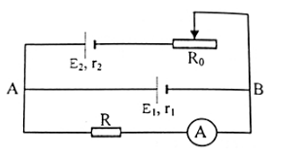
Câu 5 :
Cho mạch điện như hình vẽ: E1 = 12V, r1 =1$\Omega $, E2 = 6V, r2 = 2$\Omega $, E3 = 9V, r3 = 3$\Omega $, R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = 3$\Omega $. Hiệu điện thế UAB có giá trị là: 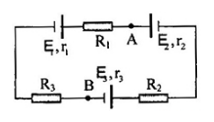
Câu 6 :
Cho mạch điện như hình vẽ: E1 = 1,9V, r1 = 0,3$\Omega $, E2 = 1,7V, r2 = 0,1$\Omega $, E3 = 1,6V, r3 = 0,1$\Omega $. Ampe kế A chỉ số 0. Điện trở R có giá trị? Coi rằng điện trở của ampe kế không đáng kể, điện trở vôn kế vô cùng lớn. 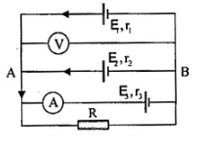
Câu 7 :
Cho mạch điện như hình vẽ: 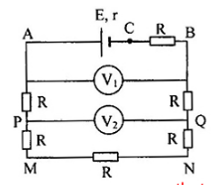 E = 24V, r = 0. Các vôn kế giống nhau. Nếu \(r = 0\) thì số chỉ vôn kế \(V_1\) là \(12V\) Số chỉ các vôn kế V2 có giá trị là:
Câu 8 :
Cho mạch điện như hình vẽ: 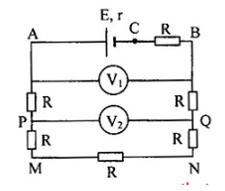 E = 24V + Khi \(r=0\) thì số chỉ vôn kế \(V_1\) là \(12V\) + Khi r ≠ 0. Số chỉ trên V1, V2 là bao nhiêu? Biết mạch ngoài không đổi và công suất tiêu thụ ở mạch ngoài đạt cực đại.
Câu 9 :
Cho mạch điện như hình vẽ: E1 = 12V, E2 = 9V, E3 = 3V, r1 = r2 = r3 = 1$\Omega $. Các điện trở R1 = R2 = R3 = 2$\Omega $. Hiệu điện thế UAB có giá trị: 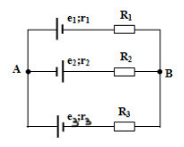
Câu 10 :
Cho mạch như hình vẽ: E1 = 24V, E2 = 6V, r1 = r2 = 1$\Omega $; R1 = 5$\Omega $; R2 = 2$\Omega $. R là biến trở. Với giá trị nào của biến trở thì công suất trên R đạt cực đại, giá trị cực đại đó là? 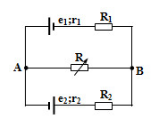
Câu 11 :
Cho mạch điện như hình vẽ: e1 = 6V, e2 = 18V, r1 = r2 = 2$\Omega $; R0 = 4$\Omega $. Đèn ghi 6V - 6W. R là biến trở. Khi R = 6$\Omega $ đèn sáng thế nào? 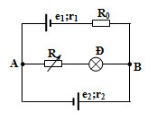
Câu 12 :
Cho mạch điện như hình vẽ: e1 = 6V, e2 = 18V, r1 = r2 = 2$\Omega $; R0 = 4$\Omega $. Đèn ghi 6V - 6W. R là biến trở. R = ? để đèn sáng bình thường 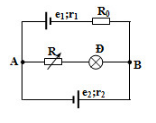
Câu 13 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu AB là ? 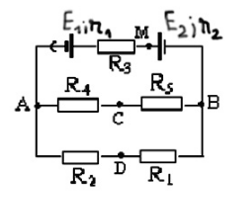
Câu 14 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu CD là ? 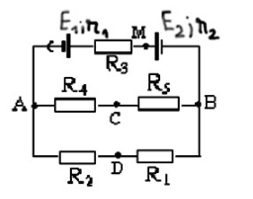
Câu 15 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu M,D là ? 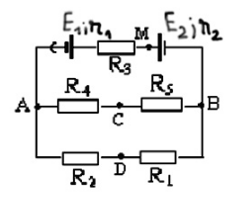
Câu 16 :
Cho sơ đồ mạch điện như hình vẽ: 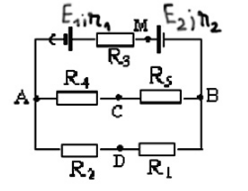 \({R_1} = 4\Omega \) , \({R_2} = 2\Omega \), \({R_3} = {R_4} = {R_5} = 6\Omega \) , \({E_1} = {\rm{ }}3V\) , \({E_2} = {\rm{ }}15V\) , \({r_1} = {r_2} = 1\Omega \). Công suất của nguồn và máy thu là?
Câu 17 :
Một mạch điện kín gồm nguồn điện \(E = 12\,\,V;\,\,r = 1\,\,\Omega \). Mạch ngoài gồm bóng đèn có ghi \(\left( {6V - 6W} \right)\) mắc nối tiếp với một biến trở. Để đèn sáng bình thường, biến trở có giá trị bằng
Câu 18 :
Biến trở \({R_x}\) mắc vào hai cực của nguồn điện có suất điện động \(E\) và điện trở trong \(r\). Điều chỉnh biến trở để công suất tỏa nhiệt của dòng điện qua nó đạt cực đại. Giá trị của công suất cực đại là
Câu 19 :
Cho mạch điện kín gồm nguồn điện có suất điện động \(E = 12V\), điện trở trong \(r = 2\Omega \) nối với mạch ngoài gồm điện trở \({R_1} = 6\Omega ,{R_2} = 4\Omega ,{R_3} = 8\Omega \) mắc theo sơ đồ như hình vẽ. Điện trở các dây nối không đáng kể. Cường độ dòng điện qua R2 xấp xỉ bằng
Câu 20 :
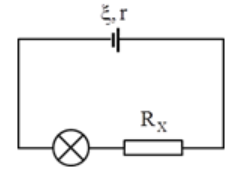
Cho mạch điện như hình vẽ. Biết E = 12V, r = 4Ω; bóng đèn thuộc loại 6V – 6W. Để đèn sáng bình thường thì giá trị của Rx là:
Câu 21 :
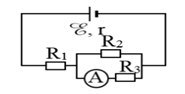
Cho mạch điện có sơ đồ như hình bên: \({\rm{E}} = 12{\rm{V}};{{\rm{R}}_1} = 4{\rm{\Omega }};{{\rm{R}}_2} = {{\rm{R}}_3} = 10{\rm{\Omega }}\) . Bỏ qua điện trở của ampe kế A và dây nối. Số chỉ của ampe kế là 0,6A. Giá trị điện trở trong r của nguồn điện là
Câu 22 :
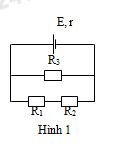
Cho mạch điện như hình 1. Biết R1 = 1\(\Omega \), R2 = 5\(\Omega \); R3 = 12\(\Omega \); E= 3V, r = 1\(\Omega \). Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu điện R1 có giá trị:
Câu 23 :
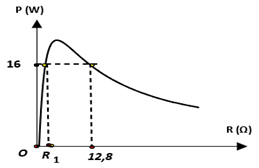
Một mạch điện kín gồm một biến trở thuần \(R,\) nguồn điện không đổi có suất điện động \(E,\) điện trở trong \(r = 8\Omega \). Đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên biến trở theo \(R\) như hình vẽ bên. Giá trị của \(R_1\) là
Câu 24 :
Một mạch điện kín gồm một nguồn điện có suất điện động E và điện trở trong r. Mạch ngoài là một biến trở R. Khi giá trị của biến trở tăng từ \(2\Omega \) đến \(8\Omega \) thì hiệu suất của nguồn điện tăng 1,6 lần. Điện trở trong của nguồn điện bằng
Câu 25 :
Ghép 3 pin giống nhau song song mỗi pin có suất điện động 3V và điện trở trong \(1\Omega .\) Suất điện động và điện trở trong của bộ pin là
Câu 26 :
Nguồn \(E = 20V,r = 1\Omega \) nối với mạch ngoài gồm \({R_1} = 0,5\Omega \) và \({R_2}\) mắc song song. Tìm \({R_2}\) để công suất tiêu thụ trên \({R_2}\) đạt cực đại.
Câu 27 :
Một mạch điện kín gồm nguồn điện có suất điện động là E, điện trở trong là r và mạch ngoài là biến trở R. Khi biến trở có giá trị \({R_1}\) hoặc \({R_2}\) thì công suất mạch ngoài là bằng nhau. Khi biến trở có giá trị \({R_0}\) thì công suất mạch ngoài là cực đại. Khi đó ta có:
Lời giải và đáp án
Câu 1 :
Cho mạch điện như hình vẽ: \({E_1} = 8V\), \({r_1} = 1,2\Omega \), \({E_2} = 4V\), \({r_2} = 0,4\Omega \), \(R = 28,4\Omega \), \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch và chiều của nó là? 
Đáp án : A Phương pháp giải :
+ Giả sử chiều dòng điện + Áp dụng định luật Ôm cho đoạn mạch Lời giải chi tiết :
Giả sử dòng điện trong đoạn mạch có chiều từ A đến B. Khi đó E1 là máy phát, E2 là máy thu. + Áp dụng định luật Ôm cho đoạn mạch AB, ta có: \(I = \dfrac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \dfrac{1}{3}A\) Nhận thấy I > 0 => điều giả sử là đúng hay dòng điện có chiều từ A đến B
Câu 2 :
Cho mạch điện như hình vẽ:  \({E_1} = 8V,{r_1} = 1,2\Omega \), \({E_2} = 4V,{r_2} = 0,4\Omega \), \(R = 28,4\Omega\), \({U_{AB}} = 6V\). Hiệu điện thế \({U_{AC}}\) và \({U_{CB}}\) là:
Đáp án : D Phương pháp giải :
+ Giả sử chiều dòng điện + Áp dụng định luật Ôm cho đoạn mạch Lời giải chi tiết :
Giả sử dòng điện trong đoạn mạch có chiều từ A đến B. Khi đó E1 là máy phát, E2 là máy thu. Áp dụng định luật Ôm cho đoạn mạch AB, ta có: \(I = \dfrac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \dfrac{1}{3}A\) Nhận thấy I > 0 => điều giả sử là đúng hay dòng điện có chiều từ A đến B Hiệu điện thế giữa hai điểm A và C: \({U_{AC}} = - {\rm{ }}{E_1} + {\rm{ }}I{r_1} = - 8{\rm{ }} + \dfrac{1}{3}.1,2 = - 7,6V\) Hiệu điện thế giữa hai điểm C và B: \({U_{CB}} = {E_2} + {\rm{ }}I({r_2} + R) = 4 + \dfrac{1}{3}.(0,4 + 28,4) = 13,6V\)
Câu 3 :
Cho mạch điện như hình vẽ: E1 = 2,1V, E2 = 1,5V, r1 = r2 = 0, R1 = R3 = 10$\Omega $; R2 = 20$\Omega $ Cường độ dòng điện qua R3 là: 
Đáp án : C Phương pháp giải :
+ Giả sử chiều dòng điện + Áp dụng định luật Ôm cho đoạn mạch Lời giải chi tiết :
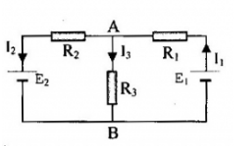 Giả sử chiều các dòng điện đi như hình Ta có: \(\left\{ \begin{array}{l}{U_{AB}} = 2,1 - 10{I_1}\\{U_{AB}} = 20{I_2} + 1,5\\{U_{AB}} = 10{I_3}\end{array} \right. \to \left\{ \begin{array}{l}2,1 - 10{I_1} = 10{I_3}\\20{I_2} + 1,5 = 10{I_3}\end{array} \right. \to \left\{ \begin{array}{l}10{I_1} + 10{I_3} = 2,1{\rm{ (1)}}\\20{I_2} - 10{I_3} = - 1,5{\rm{ (2)}}\end{array} \right.\) Tại nút A, ta có: I1 = I2 + I3 => I1 - I2 - I3 = 0 (3) Từ (1), (2) và (3), ta có: I1 = 0,096A, I2 = -0,018A, I3 = 0,114A Vì I2 < 0 => Chiều I2 ngược lại với chiều giả sử ban đầu
Câu 4 :
Cho mạch điện như hình vẽ: R = 10$\Omega $, r1 = r2 = 1$\Omega $, RA = 0. Khi dịch chuyển con chạy đến giá trị R0 số chỉ của ampe kế không đổi bằng 1A. Xác định E1; E2 ? 
Đáp án : B Lời giải chi tiết :
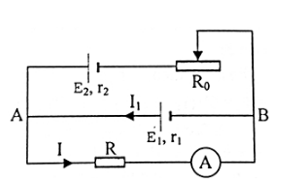 Để số chỉ ampe kế không phụ thuộc vào sự thay đổi của R0 thì dòng điện qua R0 phải bằng 0. Khi đó, chỉ có dòng qua E1 và R => E1 phải là máy phát và lúc này ta cũng có: I1 = IA = 1A Chiều dòng điện như hình vẽ UAB = IR = 1.10 =10V = E2 UAB = E1 - I1r1 => E1 = UAB + I1r1 = 10 + 1.1 = 11V
Câu 5 :
Cho mạch điện như hình vẽ: E1 = 12V, r1 =1$\Omega $, E2 = 6V, r2 = 2$\Omega $, E3 = 9V, r3 = 3$\Omega $, R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = 3$\Omega $. Hiệu điện thế UAB có giá trị là: 
Đáp án : C Phương pháp giải :
+ Giả sử chiều dòng điện + Áp dụng định luật Ôm cho đoạn mạch Lời giải chi tiết :
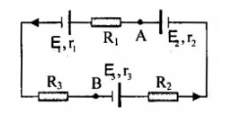 Giả sử chiều các dòng điện trong mạch như hình: Áp dụng định luật Ôm cho mạch kín ta có: \(I = \frac{{{E_2} + {E_3} - {E_1}}}{{{R_1} + {R_2} + {R_3} + {r_1} + {r_2} + {r_3}}} = \frac{{6 + 9 - 12}}{{4 + 2 + 3 + 1 + 2 + 3}} = 0,2A\) Nhận thấy I > 0 => chiều dòng điện giả sử là đúng Hiệu điện thế giữa hai điểm A,B là: \({U_{AB}} = {E_1} + I({R_1} + {R_3} + {r_1}) = 12 + 0,2(4 + 3 + 1) = 13,6V\)
Câu 6 :
Cho mạch điện như hình vẽ: E1 = 1,9V, r1 = 0,3$\Omega $, E2 = 1,7V, r2 = 0,1$\Omega $, E3 = 1,6V, r3 = 0,1$\Omega $. Ampe kế A chỉ số 0. Điện trở R có giá trị? Coi rằng điện trở của ampe kế không đáng kể, điện trở vôn kế vô cùng lớn. 
Đáp án : D Lời giải chi tiết :
Số chỉ ampe kế bằng 0 => dòng điện không qua ampe kế => UAB = E3 = 1,6V Vì vôn kế có điện trở vô cùng lớn nên dòng điện cũng không qua vôn kế. Vẽ lại mạch, ta được : 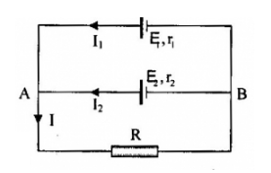 Ta có: \(\left\{ \begin{array}{l}{U_{AB}} = {E_1} - {I_1}{r_1}\\{U_{AB}} = {E_2} - {I_2}{r_2}\\{U_{AB}} = IR\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}1,6 = 1,9 - 0,3{I_1}\\1,6 = 1,7 - 0,1{I_2}\\1,6 = IR\end{array} \right. \to \left\{ \begin{array}{l}{I_1} = 1(A)\\{I_2} = 1(A)\end{array} \right.\) I = I1 + I2 = 1 + 1 = 2(A) => R = 1,6/2 = 0,8$\Omega $
Câu 7 :
Cho mạch điện như hình vẽ:  E = 24V, r = 0. Các vôn kế giống nhau. Nếu \(r = 0\) thì số chỉ vôn kế \(V_1\) là \(12V\) Số chỉ các vôn kế V2 có giá trị là:
Đáp án : D Lời giải chi tiết :
- Giả sử RV vô cùng lớn: RV = ∞ + Số chỉ trên V1 là: \({U_1} = 5R\dfrac{E}{{6R}} = \dfrac{5}{6}E = \dfrac{5}{6}.24 = 20V\) Điều này trái với giả thiết => điều giả sử là sai hay RV hữu hạn. - Ta có: UAC = 24V => UBC = 12V \( \to {R_{CMNB}} = R \\\leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R\) Với \({R_{PQ}} = \dfrac{{3R.{R_V}}}{{3R + {R_V}}} \to {R_V} = 1,5R\) Số chỉ trên V2 : + \({U_2} = \dfrac{{{U_{BC}}}}{{3R}}R = 4V\)
Câu 8 :
Cho mạch điện như hình vẽ:  E = 24V + Khi \(r=0\) thì số chỉ vôn kế \(V_1\) là \(12V\) + Khi r ≠ 0. Số chỉ trên V1, V2 là bao nhiêu? Biết mạch ngoài không đổi và công suất tiêu thụ ở mạch ngoài đạt cực đại.
Đáp án : C Lời giải chi tiết :
+ Khi r = 0 - Giả sử RV vô cùng lớn: RV = ∞ + Số chỉ trên V1 là: \({U_1} = 5R\dfrac{E}{{6R}} = \dfrac{5}{6}E = \dfrac{5}{6}.24 = 20V\) Điều này trái với giả thiết => điều giả sử là sai hay RV hữu hạn. - Ta có: UAC = 24V => UBC = 12V \( \to {R_{CMNB}} = R \\\leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R\) Với \({R_{PQ}} = \dfrac{{3R.{R_V}}}{{3R + {R_V}}} \to {R_V} = 1,5R\) + Khi r khác 0 Mạch ngoài tiêu thụ công suất cực đại khi: RN = r Ta có: \({R_{AB}} = R \leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R \to {R_N} = R + {R_{AB}} = 2R\) Số chỉ trên V1 là : \({U_1}' = {U_{AB}} = \dfrac{E}{{R + {R_{AB}} + r}}{R_{AB}} = 6V\) Số chỉ trên V2 là: \({U_1}' = {U_{PQ}} = \dfrac{{{U_{AB}}}}{{{R_{APQB}}}}{R_{PQ}} = 2V\)
Câu 9 :
Cho mạch điện như hình vẽ: E1 = 12V, E2 = 9V, E3 = 3V, r1 = r2 = r3 = 1$\Omega $. Các điện trở R1 = R2 = R3 = 2$\Omega $. Hiệu điện thế UAB có giá trị: 
Đáp án : A Lời giải chi tiết :
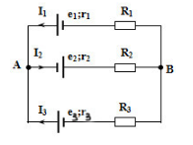 Giả sử chiều dòng điện như hình vẽ Coi AB là hai cực của nguồn tương đương với A - cực dương, mạch ngoài coi như có điện trở vô cùng lớn. \(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_1}}} + \frac{1}{{{r_2} + {R_2}}} + \frac{1}{{{r_3} + {R_3}}} = \frac{3}{{{r_1} + {R_1}}} \to {r_b} = 1\Omega \) \({E_b} = \frac{{\frac{{{E_1}}}{{{r_1} + {R_1}}} - \frac{{{E_2}}}{{{r_2} + {R_2}}} + \frac{{{E_3}}}{{{r_3} + {R_3}}}}}{{\frac{1}{{{r_b}}}}} = 2V = {U_{AB}}\)
Câu 10 :
Cho mạch như hình vẽ: E1 = 24V, E2 = 6V, r1 = r2 = 1$\Omega $; R1 = 5$\Omega $; R2 = 2$\Omega $. R là biến trở. Với giá trị nào của biến trở thì công suất trên R đạt cực đại, giá trị cực đại đó là? 
Đáp án : B Lời giải chi tiết :
Ta xét nguồn tương đương gồm hai nhánh chứa hai nguồn E1 và E2 Giả sử cực dương của nguồn tương đương ở A, chiều dòng điện như hình vẽ: 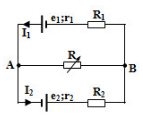 Biến trở R là mạch ngoài: \(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_1}}} + \frac{1}{{{r_2} + {R_2}}} \to {r_b} = 2\Omega \) \({E_b} = \frac{{\frac{{{E_1}}}{{{r_1} + {R_1}}} - \frac{{{E_2}}}{{{r_2} + {R_2}}}}}{{\frac{1}{{{r_b}}}}} = 4V = {U_{AB}}\) Mạch tương đương: 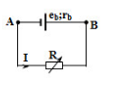 Để công suất trên R cực đại thì : R = rb = 2$\Omega $ \({P_{{\rm{max}}}} = \frac{{E_b^2}}{{4{{\rm{r}}_b}}} = 2{\rm{W}}\)
Câu 11 :
Cho mạch điện như hình vẽ: e1 = 6V, e2 = 18V, r1 = r2 = 2$\Omega $; R0 = 4$\Omega $. Đèn ghi 6V - 6W. R là biến trở. Khi R = 6$\Omega $ đèn sáng thế nào? 
Đáp án : C Phương pháp giải :
+ Áp dụng định luật Ôm cho đoạn mạch + Áp dụng biểu thức: P = UI = U2/R Lời giải chi tiết :
Khi R = 6$\Omega $. Ta xét nguồn điện tương đương gồm hai nhánh chứa hai nguồn e1 và e2. Giả sử cực dương của nguồn tương đương ở A. Biến trở R và đèn là mạch ngoài. \(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_0}}} + \frac{1}{{{r_2}}} \to {r_b} = 1,5\Omega \) \({e_b} = \frac{{\frac{{{e_1}}}{{{r_1} + {R_0}}} - \frac{{{e_2}}}{{{r_2}}}}}{{\frac{1}{{{r_b}}}}} = - 12V < 0\) => Cực dương của nguồn tương đương ở B. Ta có điện trở của đèn: \({R_D} = \frac{{{U^2}}}{P} = \frac{{{6^2}}}{6} = 6\Omega \) Cường độ dòng điện định mức của đèn: \({I_{dm}} = \frac{P}{U} = \frac{6}{6} = 1A\) \({I_d} = I = \frac{{{e_b}}}{{R + {R_d} + {r_b}}} = \frac{8}{9} < {I_{dm}}\) => Đèn sáng yếu
Câu 12 :
Cho mạch điện như hình vẽ: e1 = 6V, e2 = 18V, r1 = r2 = 2$\Omega $; R0 = 4$\Omega $. Đèn ghi 6V - 6W. R là biến trở. R = ? để đèn sáng bình thường 
Đáp án : C Phương pháp giải :
+ Áp dụng định luật Ôm cho đoạn mạch + Áp dụng biểu thức: P = UI = U2/R Lời giải chi tiết :
Khi R = 6$\Omega $. Ta xét nguồn điện tương đương gồm hai nhánh chứa hai nguồn e1 và e2. Giả sử cực dương của nguồn tương đương ở A. Biến trở R và đèn là mạch ngoài. \(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_0}}} + \frac{1}{{{r_2}}} \to {r_b} = 1,5\Omega \) \({e_b} = \frac{{\frac{{{e_1}}}{{{r_1} + {R_0}}} - \frac{{{e_2}}}{{{r_2}}}}}{{\frac{1}{{{r_b}}}}} = - 12V < 0\) => Cực dương của nguồn tương đương ở B. Ta có điện trở của đèn: \({R_D} = \frac{{{U^2}}}{P} = \frac{{{6^2}}}{6} = 6\Omega \) Cường độ dòng điện định mức của đèn: \({I_{dm}} = \frac{P}{U} = \frac{6}{6} = 1A\) \({I_d} = I = \frac{{{e_b}}}{{R + {R_d} + {r_b}}}\) Để đèn sáng bình thường thì I = Iđm \({I_d} = I = \frac{{{e_b}}}{{R + {R_d} + {r_b}}} = {I_{dm}} = 1A \leftrightarrow \frac{{12}}{{R + 6 + 1,5}} = 1 \to R = 4,5\Omega \)
Câu 13 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu AB là ? 
Đáp án : A Lời giải chi tiết :
Ta có: Mạch gồm: (R4 nt R5) // (R2 nt R1) R45 = R4 + R5 = 12$\Omega $ R12 = R1 +R2 = 4 + 2 = 6$\Omega $ + \({R_N} = \frac{{{R_{34}}{R_{12}}}}{{{R_{34}} + {R_{12}}}} = \frac{{12.6}}{{12 + 6}} = 4\Omega \) rb = r1 + r2 + R3 = 8$\Omega $ Eb = E2 - E1 = 12V \(I = \frac{{{E_b}}}{{{R_N} + {r_b}}} = 1A\) UAB = I.RN = 4V
Câu 14 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu CD là ? 
Đáp án : C Lời giải chi tiết :
Ta có: Mạch gồm: (R4 nt R5) // (R2 nt R1) R45 = R4 + R5 = 12$\Omega $ R12 = R1 +R2 = 4 + 2 = 6$\Omega $ + \({R_N} = \frac{{{R_{34}}{R_{12}}}}{{{R_{34}} + {R_{12}}}} = \frac{{12.6}}{{12 + 6}} = 4\Omega \) rb = r1 + r2 + R3 = 8$\Omega $ Eb = E2 - E1 = 12V \(I = \frac{{{E_b}}}{{{R_N} + {r_b}}} = 1A\) UAB = I.RN = 4V Ta có: UCD = VC - VD = VC - VA + VA - VD = UAD - UAC = U2 - U4 + \({U_2} = {I_2}{R_2} = \frac{{{U_{AB}}}}{{{R_1} + {R_2}}}{R_2} = \frac{4}{3}V\) + \({U_4} = {I_4}{R_4} = \frac{{{U_{AB}}}}{{{R_4} + {R_5}}}{R_4} = 2V\) \( = > {\rm{ }}{U_{CD}} = \frac{4}{3} - 2 = - \frac{2}{3}V\)
Câu 15 :
Cho sơ đồ mạch điện như hình vẽ: R1 = 4$\Omega $, R2 = 2$\Omega $, R3 = R4 = R5 = 6$\Omega $, E1 = 3V, E2 = 15V, r1 = r2 = 1$\Omega $ Hiệu điện thế hai đầu M,D là ? 
Đáp án : C Lời giải chi tiết :
Ta có: Mạch gồm: (R4 nt R5) // (R2 nt R1) R45 = R4 + R5 = 12$\Omega $ R12 = R1 +R2 = 4 + 2 = 6$\Omega $ + \({R_N} = \frac{{{R_{34}}{R_{12}}}}{{{R_{34}} + {R_{12}}}} = \frac{{12.6}}{{12 + 6}} = 4\Omega \) rb = r1 + r2 + R3 = 8$\Omega $ Eb = E2 - E1 = 12V \(I = \frac{{{E_b}}}{{{R_N} + {r_b}}} = 1A\) UAB = I.RN = 4V Ta có: UMD = VM - VD = VM - VA + VA - VD = UMA + UAD + UMA = E1 + I(r1 +R3) =10V + \({U_{AD}} = {U_2} = {I_2}{R_2} = \frac{{{U_{AB}}}}{{{R_1} + {R_2}}}{R_2} = \frac{4}{3}V\) \( \to {U_{MD}} = 10 + \frac{4}{3} = \frac{{34}}{3}V\)
Câu 16 :
Cho sơ đồ mạch điện như hình vẽ:  \({R_1} = 4\Omega \) , \({R_2} = 2\Omega \), \({R_3} = {R_4} = {R_5} = 6\Omega \) , \({E_1} = {\rm{ }}3V\) , \({E_2} = {\rm{ }}15V\) , \({r_1} = {r_2} = 1\Omega \). Công suất của nguồn và máy thu là?
Đáp án : D Phương pháp giải :
+ Áp dụng định luật Ôm cho đoạn mạch + Áp dụng biểu thức : \(P = UI\) Lời giải chi tiết :
Ta có: Mạch gồm: \(\left( {{R_4}nt{\rm{ }}{R_5}} \right){\rm{ }}//{\rm{ }}\left( {{R_2}nt{\rm{ }}{R_1}} \right)\) \({R_{45}} = {R_4} + {R_5} = 12\Omega \) \({R_{12}} = {R_1} + {R_2} = 4 + 2 = 6\Omega \) + \({R_N} = \dfrac{{{R_{45}}{R_{12}}}}{{{R_{45}} + {R_{12}}}} = \dfrac{{12.6}}{{12 + 6}} = 4\Omega \) \({r_b} = {r_1} + {r_2} + {R_3} = 8\Omega \) \({E_b} = {\rm{ }}{E_2} - {\rm{ }}{E_1} = {\rm{ }}12V\) \(I = \dfrac{{{E_b}}}{{{R_N} + {r_b}}} = 1A\) Ta có: + Công suất của nguồn: \({P_N} = {\rm{ }}I.{E_2} = {\rm{ }}1.15{\rm{ }} = {\rm{ }}15W\) + Công suất của máy thu: \({P_{MT}} = {\rm{ }}I.{E_1} + {\rm{ }}{I^2}{r_1} = {\rm{ }}1.{\rm{ }}3{\rm{ }} + {\rm{ }}1.{\rm{ }}1{\rm{ }} = {\rm{ }}4W\)
Câu 17 :
Một mạch điện kín gồm nguồn điện \(E = 12\,\,V;\,\,r = 1\,\,\Omega \). Mạch ngoài gồm bóng đèn có ghi \(\left( {6V - 6W} \right)\) mắc nối tiếp với một biến trở. Để đèn sáng bình thường, biến trở có giá trị bằng
Đáp án : C Phương pháp giải :
Cường độ dòng điện trong mạch: \(I = \dfrac{E}{{R + {R_d} + r}}\) Đèn sáng bình thường khi: \({I_d} = {I_{dm}}\) Lời giải chi tiết :
Điện trở của đèn là: \({R_d} = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}} = \dfrac{{{6^2}}}{6} = 6\,\,\left( \Omega \right)\) Cường độ dòng điện định mức của đèn là: \({I_{dm}} = \dfrac{{{P_{dm}}}}{{{U_{dm}}}} = \dfrac{6}{6} = 1\,\,\left( A \right)\) Cường độ dòng điện trong mạch là: \(I = \dfrac{E}{{R + {R_d} + r}}\) Để đèn sáng bình thường, ta có: \(I = {I_{dm}} \Rightarrow \dfrac{E}{{R + {R_d} + r}} = {I_{dm}} \Rightarrow \dfrac{{12}}{{R + 6 + 1}} = 1 \Rightarrow R = 5\,\,\left( \Omega \right)\)
Câu 18 :
Biến trở \({R_x}\) mắc vào hai cực của nguồn điện có suất điện động \(E\) và điện trở trong \(r\). Điều chỉnh biến trở để công suất tỏa nhiệt của dòng điện qua nó đạt cực đại. Giá trị của công suất cực đại là
Đáp án : D Phương pháp giải :
Định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{R + r}}\) Công suất: \(P = {I^2}R\) Áp dụng bất đẳng thức Cô - si Lời giải chi tiết :
Cường độ dòng điện qua mạch là: \(I = \dfrac{E}{{{R_x} + r}}\) Công suất tỏa nhiệt trên biến trở là: \(P = {I^2}R = \dfrac{{{E^2}}}{{{{\left( {{R_x} + r} \right)}^2}}}{R_x} = \dfrac{{{E^2}}}{{{{\left( {\sqrt {{R_x}} + \dfrac{r}{{\sqrt {{R_x}} }}} \right)}^2}}}\) Để \({P_{max}}\) thì \(\left( {\sqrt R + \dfrac{r}{{\sqrt R }}} \right)\) nhỏ nhất. Áp dụng bất đẳng thức Cô - si, ta có: \(\left( {\sqrt {{R_x}} + \dfrac{r}{{\sqrt {{R_x}} }}} \right) \ge 2\sqrt r \) Dấu “=” xảy ra khi \(\sqrt {{R_x}} \, = \,\dfrac{r}{{\sqrt {{R_x}} }}\,\, \Rightarrow \,{R_x}\, = \,r\) Khi đó: \({P_{max}} = \dfrac{{{E^2}}}{{4r}} = \dfrac{{{E^2}}}{{4{R_x}}}\)
Câu 19 :
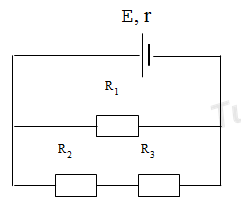
Cho mạch điện kín gồm nguồn điện có suất điện động \(E = 12V\), điện trở trong \(r = 2\Omega \) nối với mạch ngoài gồm điện trở \({R_1} = 6\Omega ,{R_2} = 4\Omega ,{R_3} = 8\Omega \) mắc theo sơ đồ như hình vẽ. Điện trở các dây nối không đáng kể. Cường độ dòng điện qua R2 xấp xỉ bằng
Đáp án : D Phương pháp giải :
+ Sử dụng biểu thức xác định điện trở của mạch có các điện trở mắc nối tiếp và song song. + Áp dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\) Lời giải chi tiết :
Ta có mạch ngoài gồm \(\left( {{R_2}nt{R_3}} \right)//{R_1}\) \({R_{23}} = {R_2} + {R_3} = 4 + 8 = 12\Omega \) \({R_N} = \dfrac{{{R_{23}}{R_1}}}{{{R_{23}} + {R_1}}} = \dfrac{{12.6}}{{12 + 6}} = 4\Omega \) Cường độ dòng điện qua mạch: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{4 + 2}} = 2A\) Hiệu điện thế mạch ngoài: \({U_N} = I.{R_N} = 2.4 = 8V\) Lại có: \({U_1} = {U_{23}} = {U_N}\) \( \Rightarrow {I_{23}} = \dfrac{{{U_{23}}}}{{{R_{23}}}} = \dfrac{{{U_N}}}{{{R_{23}}}} = \dfrac{8}{{12}} = 0,67A\) Cường độ dòng điện qua \({R_2}\) là \({I_2} = {I_{23}} = 0,67A\)
Câu 20 :
Cho mạch điện như hình vẽ. Biết E = 12V, r = 4Ω; bóng đèn thuộc loại 6V – 6W. Để đèn sáng bình thường thì giá trị của Rx là:
Đáp án : D Phương pháp giải :
Điện trở của bóng đèn: \({R_d} = \dfrac{{U_d^2}}{{{P_d}}}\) Đèn sáng bình thường khi: \({I_d} = {I_{dm}} = \dfrac{{{P_d}}}{{{I_d}}}\) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}} = \dfrac{E}{{r + \left( {{R_d} + {R_x}} \right)}}\) Để đèn sáng bình thường thì: \(I = {I_{dm}} \Rightarrow {R_x}\) Lời giải chi tiết :
Điện trở của bóng đèn: \({R_d} = \dfrac{{U_d^2}}{{{P_d}}} = \dfrac{{{6^2}}}{6} = 6\Omega \) Cường độ định mức qua đèn là: \({I_{dm}} = \dfrac{{{P_d}}}{{{I_d}}} = \dfrac{6}{6} = 1A\) Cường độ dòng điện chạy trong mạch: \(I = \dfrac{E}{{r + {R_N}}} = \dfrac{E}{{r + \left( {{R_d} + {R_x}} \right)}} = \dfrac{{12}}{{4 + 6 + {R_x}}} = \dfrac{{12}}{{10 + {R_x}}}\) Để đèn sáng bình thường thì: \(I = {I_{dm}} \Leftrightarrow \dfrac{{12}}{{10 + {R_x}}} = 1 \Rightarrow {R_x} = 2\Omega \)
Câu 21 :
Cho mạch điện có sơ đồ như hình bên: \({\rm{E}} = 12{\rm{V}};{{\rm{R}}_1} = 4{\rm{\Omega }};{{\rm{R}}_2} = {{\rm{R}}_3} = 10{\rm{\Omega }}\) . Bỏ qua điện trở của ampe kế A và dây nối. Số chỉ của ampe kế là 0,6A. Giá trị điện trở trong r của nguồn điện là
Đáp án : D Phương pháp giải :
Định luật Ôm đối với toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\) Đối với đoạn mạch mắc nối tiếp: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2}\\I = {I_1} = {I_2}\\U = {U_1} + {U_2}\end{array} \right.\) Đối với đoạn mạch mắc song song: \(\left\{ \begin{array}{l}{R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\I = {I_1} + {I_2}\\U = {U_1} = {U_2}\end{array} \right.\) Lời giải chi tiết :
Mạch ngoài gồm: \({R_1}\,\,nt\,\,\left( {{R_2}\,\,//\,{R_3}} \right)\) Điện trở tương đương của mạch ngoài là: \({R_N} = {R_1} + {R_{23}} = {R_1} + \dfrac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = 4 + \dfrac{{10.10}}{{10 + 10}} = 9\Omega \) Số chỉ của ampe kế là 0,6A \( \Rightarrow {I_3} = 0,6A \Rightarrow {U_3} = {I_3}{R_3} = 0,6.10 = 6V\) Do \({R_1}{\mkern 1mu} {\mkern 1mu} nt{\mkern 1mu} {\mkern 1mu} \left( {{R_2}{\mkern 1mu} {\mkern 1mu} //{\mkern 1mu} {R_3}} \right) \Rightarrow {U_{23}} = 6V\) \( \Rightarrow {I_{23}} = \frac{{{U_{23}}}}{{{R_{23}}}} = \frac{6}{5} = 1,2A \Rightarrow I = {I_{23}} = 1,2A\) Áp dụng định luật Ôm cho toàn mạch ta có: \(I = \dfrac{E}{{{R_N} + r}} \Leftrightarrow 1,2 = \dfrac{{12}}{{9 + r}} \Leftrightarrow 9 + r = 10 \Rightarrow r = 1\Omega \)
Câu 22 :
Cho mạch điện như hình 1. Biết R1 = 1\(\Omega \), R2 = 5\(\Omega \); R3 = 12\(\Omega \); E= 3V, r = 1\(\Omega \). Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu điện R1 có giá trị:
Đáp án : A Phương pháp giải :
Áp dụng định luật Ôm Lời giải chi tiết :
Tổng trở của mạch là: \(R=\frac{({{R}_{1}}+{{R}_{2}}).{{R}_{3}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}=4\Omega \) Dòng điện trong mạch: \(I=\frac{E}{R+r}=0,6A\) Hiệu điện thế giữa hai đầu điện R12 có giá trị: U12 = E – I.r = 2,4 (V) Dòng điện đi qua điện trở R1 là: \({{I}_{1}}=I-{{I}_{3}}=I-\frac{{{U}_{12}}}{{{R}_{3}}}=0,6-\frac{2,4}{12}=0,4(A)\) Hiệu điện thế giữa hai đầu điện R1 có giá trị: U1 = I1. R1 = 0,4 (V)
Câu 23 :
Một mạch điện kín gồm một biến trở thuần \(R,\) nguồn điện không đổi có suất điện động \(E,\) điện trở trong \(r = 8\Omega \). Đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên biến trở theo \(R\) như hình vẽ bên. Giá trị của \(R_1\) là
Đáp án : D Phương pháp giải :
Định luật Ôm: \(I = \dfrac{E}{{r + R}}\) Công suất tiêu thụ trên biến trở: \(P = {I^2}R\) Lời giải chi tiết :
Công suất tiêu thụ trên biến trở: \(P = {I^2}R = {\left( {\dfrac{E}{{r + R}}} \right)^2}.R\) Từ đồ thị ta thấy khi \(R = {R_1}\) và \(R = 12,8\Omega \) thì công suất tiêu thụ trên biến trở có cùng giá trị. Ta có: \(\begin{array}{l}{\left( {\dfrac{E}{{8 + {R_1}}}} \right)^2}.{R_1} = {\left( {\dfrac{E}{{8 + 12,8}}} \right)^2}.12,8\\ \Leftrightarrow \dfrac{{{R_1}}}{{{{\left( {8 + {R_1}} \right)}^2}}} = \dfrac{{12,8}}{{{{\left( {8 + 12,8} \right)}^2}}} \Rightarrow {R_1} = 5\Omega \end{array}\)
Câu 24 :
Một mạch điện kín gồm một nguồn điện có suất điện động E và điện trở trong r. Mạch ngoài là một biến trở R. Khi giá trị của biến trở tăng từ \(2\Omega \) đến \(8\Omega \) thì hiệu suất của nguồn điện tăng 1,6 lần. Điện trở trong của nguồn điện bằng
Đáp án : A Phương pháp giải :
Sử dụng công thức tính hiệu suất của nguồn điện: \(H = \frac{{{A_i}}}{{{A_{tp}}}} = \frac{{{U_N}It}}{{EIt}} = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\) Lời giải chi tiết :
Khi \(R = 2\Omega \) thì: \({H_1} = \frac{{{R_1}}}{{{R_1} + r}} = \frac{2}{{2 + r}}\) Khi \(R = 8\Omega \) thì: \({H_2} = \frac{{{R_2}}}{{{R_2} + r}} = \frac{8}{{8 + r}}\) Theo đề bài ta có: \({H_2} = 1,6{H_1}\) \( \Rightarrow \frac{8}{{8 + r}} = 1,6 \cdot \frac{2}{{2 + r}} \Rightarrow r = 2\Omega \)
Câu 25 :
Ghép 3 pin giống nhau song song mỗi pin có suất điện động 3V và điện trở trong \(1\Omega .\) Suất điện động và điện trở trong của bộ pin là
Đáp án : B Phương pháp giải :
Sử dụng kiến thức ghép nguồn điện thành bộ. Lời giải chi tiết :
Có 3 pin giống nhau ghép song song thì: \(\left\{ {\begin{array}{*{20}{l}}{{E_b} = E = 3\left( V \right)}\\{{r_b} = \frac{r}{3} = \frac{1}{3}\Omega }\end{array}} \right.\)
Câu 26 :
Nguồn \(E = 20V,r = 1\Omega \) nối với mạch ngoài gồm \({R_1} = 0,5\Omega \) và \({R_2}\) mắc song song. Tìm \({R_2}\) để công suất tiêu thụ trên \({R_2}\) đạt cực đại.
Đáp án : A Phương pháp giải :
Áp dụng công thức tính công suất: \(P = {I^2}R\) Lời giải chi tiết :
Điện trở mạch ngoài là: \({R_N} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{0,5.{R_2}}}{{0,5 + {R_2}}}\) Cường độ dòng điện trong mạch chính: \(I = \frac{E}{{r + {R_N}}} = \frac{{20}}{{1 + \frac{{0,5{R_2}}}{{0,5 + {R_2}}}}} = \frac{{20\left( {0,5 + {R_2}} \right)}}{{0,5 + 1,5{R_2}}}\) Hiệu điện thế mạch ngoài là: \(U = E - Ir = 20 - \frac{{20\left( {0,5 + {R_2}} \right)}}{{0,5 + 1,5{R_2}}} = \frac{{10{R_2}}}{{0,5 + 1,5{R_2}}}\) Công suất trên \({R_2}\) là: \(P = \frac{{U_2^2}}{{{R_2}}} = {\left( {\frac{{10{R_2}}}{{0,5 + 1,5{R_2}}}} \right)^2}.\frac{1}{{{R_2}}} = \frac{{100{R_2}}}{{0,{5^2} + 2.0,5.1,5{R_2} + 1,{5^2}R_2^2}}\) Chia cả tử và mẫu cho \({R_2}\) ta được: \(P = \frac{{100}}{{\frac{{0,{5^2}}}{{{R_2}}} + 1,{5^2}{R_2} + 1,5}}\) Để \({P_{\max }}\) thì mẫu \(\frac{{0,{5^2}}}{{{R_2}}} + 1,{5^2}{R_2} + 1,5\) min Áp dụng bất dẳng thức Cô-si ta có: \(\frac{{0,{5^2}}}{{{R_2}}} + 1,{5^2}{R_2} \ge 2.\sqrt {\frac{{0,{5^2}}}{{{R_2}}}.1,{5^2}{R_2}} {\rm{ \;}} = 1,5\) Vậy \({P_{\max }}\) khi \(\frac{{0,{5^2}}}{{{R_2}}} = 1,{5^2}{R_2} \Rightarrow {R_2} = \frac{1}{3}{\mkern 1mu} \Omega \)
Câu 27 :
Một mạch điện kín gồm nguồn điện có suất điện động là E, điện trở trong là r và mạch ngoài là biến trở R. Khi biến trở có giá trị \({R_1}\) hoặc \({R_2}\) thì công suất mạch ngoài là bằng nhau. Khi biến trở có giá trị \({R_0}\) thì công suất mạch ngoài là cực đại. Khi đó ta có:
Đáp án : D Phương pháp giải :
Áp dụng công thức: \(P = {\left( {\frac{E}{{r + R}}} \right)^2}.R\) Lời giải chi tiết :
Khi biến trở có giá trị \({R_1}\) thì: \({P_1} = {\left( {\frac{E}{{r + {R_1}}}} \right)^2}.{R_1}\) Khi biến trở có giá trị \({R_2}\) thì: \({P_2} = {\left( {\frac{E}{{r + {R_2}}}} \right)^2}.{R_2}\) Hai giá trị biến trở đều cho mạch có cùng công suất nên: \(\begin{array}{l}{P_1} = {P_2} \Leftrightarrow {\left( {\frac{E}{{r + {R_1}}}} \right)^2}.{R_1} = {\left( {\frac{E}{{r + {R_2}}}} \right)^2}.{R_2}\\ \Rightarrow \frac{{{R_1}}}{{{{\left( {r + {R_1}} \right)}^2}}} = \frac{{{R_2}}}{{{{\left( {r + {R_2}} \right)}^2}}} \Rightarrow \sqrt {{R_1}} \left( {r + {R_2}} \right) = \sqrt {{R_2}} \left( {r + {R_1}} \right) \Rightarrow r = \sqrt {{R_1}{R_2}} \end{array}\) Khi biến trở có giá trị \({R_0}\) thì mạch ngoài có công suất lớn nhất: \(\begin{array}{*{20}{l}}{P = {I^2}R = \frac{{{E^2}.{R_0}}}{{{{\left( {{R_0} + r} \right)}^2}}} = \frac{{{E^2}}}{{2r + \frac{{{r^2}}}{R} + R}}}\\{{P_{\max }} \Leftrightarrow {{\left( {\frac{{{r^2}}}{{{R_0}}} + {R_0}} \right)}_{\max }} \Leftrightarrow {R_0} = r = \sqrt {{R_1}{R_2}} }\end{array}\)
|



















Danh sách bình luận