Trắc nghiệm Bài 29. Định luật bảo toàn động lượng - Vật lí 10 Kết nối tri thứcĐề bài
Câu 1 :
Tổng động lượng trong một hệ kín luôn
Câu 2 :
Đâu là biểu thức đúng của định luật bảo toàn động lượng?
Câu 3 :
Vecto động lượng là vecto
Câu 4 :
Một vật chuyển động với vận tốc tăng dần có
Câu 5 :
Một viên đạn đang bay với vận tốc 10 m/s thì nổ thành hai mảnh. Mảnh thứ nhất, chiếm 60% khối lượng của quả lựu đạn và tiếp tục bay theo hướng cũa với vận tốc 25 m/s. Tốc độ và hướng chuyển động của mảnh thứ hai là?
Câu 6 :
Hai vật có khối lượng m1 và m2 chuyển động ngược hướng nhau với tốc độ 6 m/s và 2 m/s tới va chạm vào nhau. Sau va chạm, cả hai đều bị bật ngược trở lại với độ lớn vận tốc bằng nhau và bằng 4 m/s. Bỏ qua ma sát. Tỉ số \(\frac{{{m_1}}}{{{m_2}}}\) bằng:
Câu 7 :
Viên đạn khối lượng 20 g đang bay với vận tốc 600 m/s thì gặp một cánh cửa thép. Đạn xuyên qua cửa trong thời gian 0,002 s. Sau khi xuyên qua tường vận tốc của đạn còn 300 m/s. Lực cản trung bình của cửa tác dụng lên đạn có độ lớn bằng?
Câu 8 :
Một đầu đạn khối lượng 10 g được bắn ra khỏi nòng của một khẩu súng khối lượng 5 kg với vận tốc 600 m/s. Nếu bỏ qua khối lượng của đầu đạn thì vận tốc giật của súng là
Câu 9 :
Một quả bóng khối lượng 0,5 kg đang nằm yên thì được đá cho nó chuyển động với vận tốc 40 m/s. Xung lượng của lực tác dụng lên quả bóng bằng
Câu 10 :
Một xe chở cát có khối lượng M = 38 kg đang chạy trên một đường nằm ngang không ma sát với tốc độ 1 m/s. Một vật nhỏ có khối lượng m = 2 kg bay theo phương chuyển động của xe, cùng chiều với tốc độ 7 m/s đến chui vào cát và nằm yên trong đó. Tốc độ mới của xe bằng:
Câu 11 :
Hai xe lăn có khối lượng m1 = 300 g và m2 = 2 kg chuyển động trên mặt phẳng nằm ngang ngược hướng nhau với tốc độ tương ứng 2 m/s và 0,8 m/s. Bỏ qua mọi lực cản. Chọn chiều dương là chiều chuyển động của m1. Sau khi va chạm, hai xe dính vào nhau và chuyển động với cùng vận tốc v. Giá trị của v là:
Câu 12 :
Một viên đạn khối lượng M = 5kg đang bay theo phương ngang với vận tốc v =\( - 200\sqrt 3 \) m/s thì nổ thành hai mảnh. Mảnh thứ nhất có khối lượng m1 = 2 kg bay thẳng đứng xuống với vận tốc 500 m/s, còn mảnh thứ hai bay hợp với phương ngang góc
Câu 13 :
Một vật khối lượng 1 kg chuyển động tròn đều với tốc độ 10 m/s. Độ biến thiên động lượng của vật sau \(\frac{1}{4}\) chu kì kể từ lúc bắt đầu chuyển động bằng
Câu 14 :
Một viên đạn khối lượng 1 kg đang bay theo phương thẳng đứng với vận tốc 500 m/s thì nổ thành 2 mảnh có khối lượng bằng nhau. Mảnh thứ nhất bay theo phương ngang với vận tốc -500\(\sqrt 2 \) m/s hỏi mảnh 2 bay với tốc độ là bao nhiêu?
Câu 15 :
Một vật có khối lượng 2 kg rơi tự do xuống đất trong khoảng thời gian 0,5 s. Độ biến thiên động lượng của vật trong khoảng thời gian đó là bao nhiêu? Cho g = 10 m/s2.
Câu 16 :
Một khẩu đại bác có khối lượng 4 tấn, bắn đi một viên đạn theo phương ngang có khối lượng 10 kg với vận tốc 400 m/s Coi như lúc đầu, hệ đại bác và đạn đứng yên. Tốc độ giật lùi của đại bác ngay sau đó bằng
Câu 17 :
Một người có khối lượng 50 kg nhảy ngang với vận tốc 2 m/s lên một chiếc thuyền trôi dọc theo bờ sông với vận tốc 1 m/s. Biết khối lượng của thuyền là 173,2 kg. Tìm độ lớn vận tốc của thuyền khi người đã nhảy vào thuyền.
Câu 18 :
Một quả cầu khối lượng 2 kg chuyển động với tốc độ 3 m/s tới va chạm đàn hồi xuyên tâm vào quả cầu thứ hai khối lượng 3 kg đang chuyển động với vận tốc 1 m/s ngược chiều với quả thứ nhất. Xác định vận tốc của hai quả cầu sau va chạm. Chọn chiều dương là chiều chuyển động của quả cầu thứ nhất.
Lời giải và đáp án
Câu 1 :
Tổng động lượng trong một hệ kín luôn
Đáp án : D Phương pháp giải :
Áp dụng lí thuyết động lượng của hệ Lời giải chi tiết :
Tổng động lượng trong một hệ kín luôn bằng hằng số
Câu 2 :
Đâu là biểu thức đúng của định luật bảo toàn động lượng?
Đáp án : D Phương pháp giải :
Kiến thức về biểu thức của định luật bảo toàn Lời giải chi tiết :
\(\Delta \overrightarrow p = \overrightarrow 0 \)=>\(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} + ... = \overrightarrow {p{'_1}} + \overrightarrow {p{'_2}} + ...\)=>\({m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} + ... = {m_1}\overrightarrow {v{'_1}} + {m_2}\overrightarrow {v{'_2}} \)
Câu 3 :
Vecto động lượng là vecto
Đáp án : D Phương pháp giải :
Áp dụng lí thuyết về động lượng Lời giải chi tiết :
Vecto động lượng là vecto cùng phương, cùng chiều với vecto vận tốc
Câu 4 :
Một vật chuyển động với vận tốc tăng dần có
Đáp án : C Phương pháp giải :
Sử dụng mối liên hệ giữa vận tốc và động lượng Lời giải chi tiết :
Một vật chuyển động với vận tốc tăng dần có động lượng tăng dần
Câu 5 :
Một viên đạn đang bay với vận tốc 10 m/s thì nổ thành hai mảnh. Mảnh thứ nhất, chiếm 60% khối lượng của quả lựu đạn và tiếp tục bay theo hướng cũa với vận tốc 25 m/s. Tốc độ và hướng chuyển động của mảnh thứ hai là?
Đáp án : B Phương pháp giải :
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng của hệ được bảo toàn Lời giải chi tiết :
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng của hệ được bảo toàn: \(m\overrightarrow v = {m_1}\overrightarrow {{v_1}} + (m - {m_1})\overrightarrow {{v_2}} \) Do: \(\overrightarrow {{v_1}} \uparrow \uparrow \overrightarrow v \Rightarrow {v_2} = \frac{{mv - {m_1}{v_1}}}{{m - {m_1}}} = \frac{{(10 - 25.0,6)m}}{{(1 - 0,6)m}} = - 12,5m/s\) Dấu “-“ chứng tỏ mảnh đạn thứ hai sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Câu 6 :
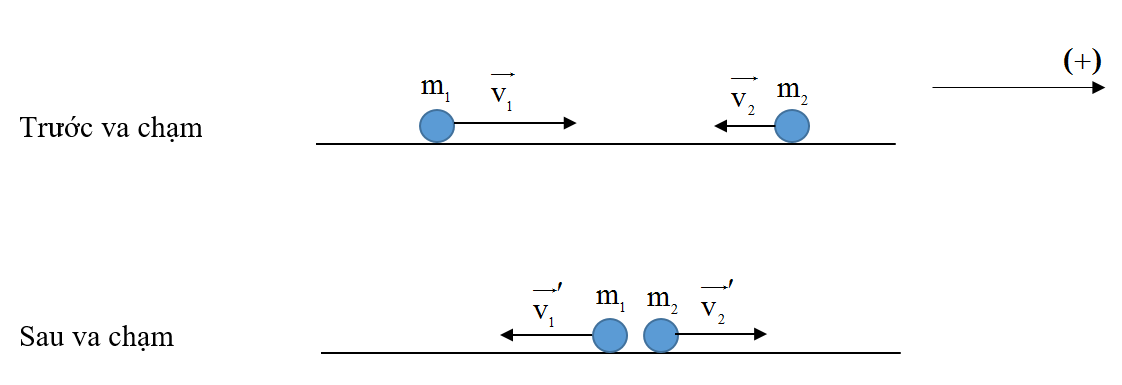
Hai vật có khối lượng m1 và m2 chuyển động ngược hướng nhau với tốc độ 6 m/s và 2 m/s tới va chạm vào nhau. Sau va chạm, cả hai đều bị bật ngược trở lại với độ lớn vận tốc bằng nhau và bằng 4 m/s. Bỏ qua ma sát. Tỉ số \(\frac{{{m_1}}}{{{m_2}}}\) bằng:
Đáp án : C Phương pháp giải :
Áp dụng định luật bảo toàn động lượng Lời giải chi tiết :
Chọn chiều dương là chiều chuyển động của m1 lúc đầu.
Trước va chạm: \(p = {m_1}{v_1} - {m_2}{v_2}\) Sau va chạm: \(p' = - {m_1}v{'_1} + {m_2}v{'_2}\) Theo phương ngang không có lực tác dụng lên hệ nên động lượng của hệ được bảo toàn. \({m_1}{v_1} - {m_2}{v_2} = {m_1}v{'_1} - {m_2}v{'_2} \Leftrightarrow 6{m_1} - 2{m_2} = - 4{m_1} + 4{m_2} \Rightarrow \frac{{{m_1}}}{{{m_2}}} = \frac{6}{{10}} = 0,6\)
Câu 7 :
Viên đạn khối lượng 20 g đang bay với vận tốc 600 m/s thì gặp một cánh cửa thép. Đạn xuyên qua cửa trong thời gian 0,002 s. Sau khi xuyên qua tường vận tốc của đạn còn 300 m/s. Lực cản trung bình của cửa tác dụng lên đạn có độ lớn bằng?
Đáp án : A Phương pháp giải :
Áp dụng công thức tính độ biến thiên động lượng Lời giải chi tiết :
Ta có: \(\overrightarrow {{F_c}} .\Delta t = m.\Delta \overrightarrow v \Rightarrow {F_c}.\Delta t = m({v_2} - {v_1}) \Rightarrow \left| {{F_c}} \right| = \frac{{m\left| {{v_2} - {v_1}} \right|}}{{\Delta t}} = \frac{{0,02.\left| {300 - 600} \right|}}{{0,002}} = 3000N\)
Câu 8 :
Một đầu đạn khối lượng 10 g được bắn ra khỏi nòng của một khẩu súng khối lượng 5 kg với vận tốc 600 m/s. Nếu bỏ qua khối lượng của đầu đạn thì vận tốc giật của súng là
Đáp án : B Phương pháp giải :
Áp dụng định luật bảo toàn động lượng Lời giải chi tiết :
Đáp án: B Chọn chiều (+) là chiều chuyển động của viên đạn. Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{p_t}} = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = \overrightarrow 0 \) Vì: \(\overrightarrow {{v_1}} \uparrow \downarrow \overrightarrow {{v_2}} \Rightarrow {m_1}{v_1} - {m_2}{v_2} = 0 \Rightarrow {v_2} = 1,2m/s\)
Câu 9 :
Một quả bóng khối lượng 0,5 kg đang nằm yên thì được đá cho nó chuyển động với vận tốc 40 m/s. Xung lượng của lực tác dụng lên quả bóng bằng
Đáp án : C Phương pháp giải :
Áp dụng công thức tính xung lượng Lời giải chi tiết :
\(\overrightarrow F .\Delta t = m.\Delta \overrightarrow v \Rightarrow F.\Delta t = m.(v - 0) = 0,5.40 = 20N.s\)
Câu 10 :
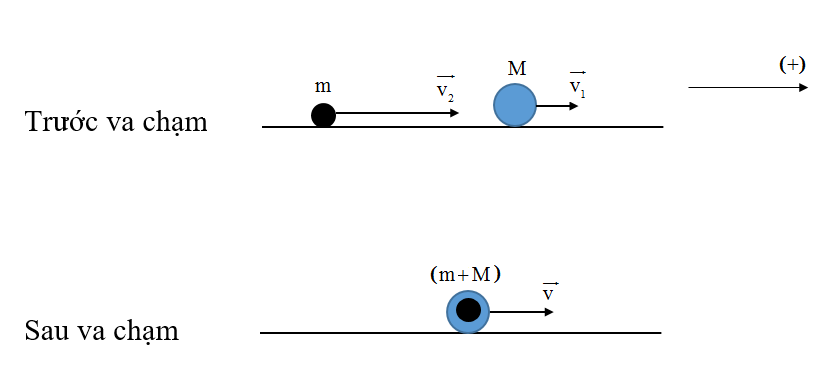
Một xe chở cát có khối lượng M = 38 kg đang chạy trên một đường nằm ngang không ma sát với tốc độ 1 m/s. Một vật nhỏ có khối lượng m = 2 kg bay theo phương chuyển động của xe, cùng chiều với tốc độ 7 m/s đến chui vào cát và nằm yên trong đó. Tốc độ mới của xe bằng:
Đáp án : A Lời giải chi tiết :
Chọn chiều dương là chiều chuyển động của xe lúc đầu. Trước va chạm: \(p = M{v_1} + m{v_2}\) Sau va chạm: \(p' = (M + m)v\) Theo phương ngang không có lực tác dụng lên hệ nên động lượng của hệ được bảo toàn. \(M{v_1} + m{v_2} = (M + m)v \Leftrightarrow v = \frac{{M{v_1} + m{v_2}}}{{M + m}} = \frac{{38.1 + 2.7}}{{38 + 2}} = 1,3m/s\)
Câu 11 :
Hai xe lăn có khối lượng m1 = 300 g và m2 = 2 kg chuyển động trên mặt phẳng nằm ngang ngược hướng nhau với tốc độ tương ứng 2 m/s và 0,8 m/s. Bỏ qua mọi lực cản. Chọn chiều dương là chiều chuyển động của m1. Sau khi va chạm, hai xe dính vào nhau và chuyển động với cùng vận tốc v. Giá trị của v là:
Đáp án : A Lời giải chi tiết :
Đổi đơn vị 300 g = 0,3 kg. Chọn chiều dương là chiều chuyển động của m1 lúc đầu. Trước va chạm: \(p = {m_1}{v_1} - {m_2}{v_2}\) Sau va chạm, giả sử v cùng chiều dương: \(p' = ({m_1} + {m_2})v\) Bỏ qua mọi lực cản nên động lượng của hệ được bảo toàn. \({m_1}{v_1} - {m_2}{v_2} = ({m_1} + {m_2})v \Rightarrow v = \frac{{{m_1}{v_1} - {m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{0,3.2 - 2.0,8}}{{0,3 + 2}} \approx - 0,43m/s\) Vậy sau va chạm, vận tốc mới của hệ là – 0,43 m/s. Dấu “-” thể hiện hướng ngược chiều dương.
Câu 12 :
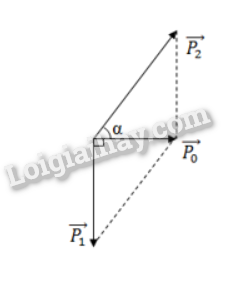
Một viên đạn khối lượng M = 5kg đang bay theo phương ngang với vận tốc v =\( - 200\sqrt 3 \) m/s thì nổ thành hai mảnh. Mảnh thứ nhất có khối lượng m1 = 2 kg bay thẳng đứng xuống với vận tốc 500 m/s, còn mảnh thứ hai bay hợp với phương ngang góc
Đáp án : D Lời giải chi tiết :
\(\tan \alpha = \frac{{{p_1}}}{{{p_0}}} = \frac{{{m_1}{v_1}}}{{mv}} = \frac{{2.500}}{{5.200\sqrt 3 }} \Rightarrow \alpha = 30^\circ \)
Câu 13 :
Một vật khối lượng 1 kg chuyển động tròn đều với tốc độ 10 m/s. Độ biến thiên động lượng của vật sau \(\frac{1}{4}\) chu kì kể từ lúc bắt đầu chuyển động bằng
Đáp án : C Phương pháp giải :
Áp dụng công thức tính độ biến thiên động lượng Lời giải chi tiết :
Khi chất điểm chuyển động trên đường tròn thì vectơ vận tốc tại mỗi vị trí có phương tiếp tuyến với quỹ đạo. Sau \(\frac{1}{4}\) chu kì kể từ lúc bắt đầu chuyển động thì góc quay của bán kính là \(\frac{\pi }{2}\) nên \(\overrightarrow {{v_1}} \bot \overrightarrow {{v_2}} \) Biến thiên động lượng của vật \(\Delta \overrightarrow p = m\overrightarrow {{v_2}} - m\overrightarrow {{v_1}} \) \( \Rightarrow \Delta p = m\sqrt {v_1^2 + v_2^2} = m\sqrt {{v^2} + {v^2}} = 1.\sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 \)kgm/s
Câu 14 :
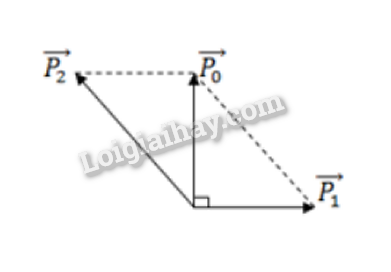
Một viên đạn khối lượng 1 kg đang bay theo phương thẳng đứng với vận tốc 500 m/s thì nổ thành 2 mảnh có khối lượng bằng nhau. Mảnh thứ nhất bay theo phương ngang với vận tốc -500\(\sqrt 2 \) m/s hỏi mảnh 2 bay với tốc độ là bao nhiêu?
Đáp án : A Phương pháp giải :
Tổng hợp động lượng của hệ Lời giải chi tiết :
Ta có: \(\begin{array}{l}p_2^2 = p_0^2 + p_1^2\\ \Rightarrow {({m_2}{v_2})^2} = {(mv)^2} + {({m_1}{v_1})^2}\\ \Rightarrow {(\frac{m}{2}.{v_2})^2} = {(mv)^2} + {(\frac{m}{2}{v_1})^2}\\ \Rightarrow {(\frac{{{v_2}}}{2})^2} = {(v)^2} + {(\frac{{{v_1}}}{2})^2}\\ \Rightarrow {v_2} = 500\sqrt 6 m/s\end{array}\)
Câu 15 :
Một vật có khối lượng 2 kg rơi tự do xuống đất trong khoảng thời gian 0,5 s. Độ biến thiên động lượng của vật trong khoảng thời gian đó là bao nhiêu? Cho g = 10 m/s2.
Đáp án : B Lời giải chi tiết :
Ta có: \(\Delta p = {p_2} - {p_1} = m({v_2} - {v_1})\) Mà \({v_1} = 0,{v_2} = gt = 10.0,5 = 5\)m/s \( \Rightarrow \Delta p = m{v_2} = 2.5 = 10\)kg.m/s
Câu 16 :
Một khẩu đại bác có khối lượng 4 tấn, bắn đi một viên đạn theo phương ngang có khối lượng 10 kg với vận tốc 400 m/s Coi như lúc đầu, hệ đại bác và đạn đứng yên. Tốc độ giật lùi của đại bác ngay sau đó bằng
Đáp án : D Phương pháp giải :
Áp dụng định luật bảo toàn động lượng cho hệ kín Lời giải chi tiết :
Khi bắn thì hệ súng đạn là hệ kín nên ta có: \(0 = {m_s}{v_s} + m{}_d{v_d} \Rightarrow {v_s} = \left| {\frac{{m{}_d{v_d}}}{{{m_s}}}} \right| = 1\)m/s
Câu 17 :
Một người có khối lượng 50 kg nhảy ngang với vận tốc 2 m/s lên một chiếc thuyền trôi dọc theo bờ sông với vận tốc 1 m/s. Biết khối lượng của thuyền là 173,2 kg. Tìm độ lớn vận tốc của thuyền khi người đã nhảy vào thuyền.
Đáp án : A Phương pháp giải :
Áp dụng định luật bảo toàn động lượng Lời giải chi tiết :
Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} = \overrightarrow p \) Vì: \(\overrightarrow {{v_2}} \bot \overrightarrow {{v_1}} \) nên \(p = \sqrt {p_1^2 + p_2^2} \Leftrightarrow ({m_1} + {m_2}).V = \sqrt {{{({m_1}{v_1})}^2} + {{({m_2}{v_2})}^2}} \Rightarrow V = \frac{{\sqrt {{{({m_1}{v_1})}^2} + {{({m_2}{v_2})}^2}} }}{{{m_1} + {m_2}}} = \frac{{\sqrt {{{(50.2)}^2} + {{(173,2.1)}^2}} }}{{(50 + 173,2)}} = 0,896\)m/s
Câu 18 :
Một quả cầu khối lượng 2 kg chuyển động với tốc độ 3 m/s tới va chạm đàn hồi xuyên tâm vào quả cầu thứ hai khối lượng 3 kg đang chuyển động với vận tốc 1 m/s ngược chiều với quả thứ nhất. Xác định vận tốc của hai quả cầu sau va chạm. Chọn chiều dương là chiều chuyển động của quả cầu thứ nhất.
Đáp án : A Phương pháp giải :
Va chạm là đàn hồi xuyên tâm nên + Áp dụng định luật bảo toàn động lượng + Động năng trước và sau va chạm bằng nhau Lời giải chi tiết :
Va chạm là đàn hồi xuyên tâm nên + Áp dụng định luật bảo toàn động lượng: \(\begin{array}{l}{m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = {m_1}\overrightarrow {v{'_1}} + {m_2}\overrightarrow {v{'_2}} \\ \Rightarrow {m_1}(\overrightarrow {{v_1}} - \overrightarrow {v{'_1}} ) = {m_2}(\overrightarrow {v{'_2}} - \overrightarrow {{v_2}} )\end{array}\) + Động năng trước và sau va chạm bằng nhau nên: \(\begin{array}{l}\frac{{{m_1}v_1^2}}{2} + \frac{{{m_2}v_2^2}}{2} = \frac{{{m_1}v{'_1}^2}}{2} + \frac{{{m_1}v{'_2}^2}}{2}\\ \Rightarrow {m_1}(v_1^2 – v{'_1}^2) = {m_2}(v{'_2}^2 - v_2^2)\\ \Rightarrow v{'_1} = \frac{{({m_1} - {m_2}).{v_1} + 2{m_2}{v_2}}}{{{m_1} + {m_2}}}\\v{'_2} = \frac{{({m_2} - {m_1}).{v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}}\end{array}\)
Chọn chiều dương là chiều chuyển động của quả cầu thứ nhất nên \({v_1} = 3m/s;{v_2} = - 1m/s\) Thay số vào ta được \(v{'_1} = - 1,8m/s;v{'_2} = 2,2m/s\)
|



















Danh sách bình luận