Trắc nghiệm Bài 25. Động năng, thế năng - Vật lí 10 Kết nối tri thứcĐề bài
Câu 1 :
Vận động viên Hoàng Xuân Vinh bắn một viên đạn có khối lượng 100 g bay ngang với vận tốc 300 m/s xuyên qua tấm bia bằng gỗ dày 5 cm. Sau khi xuyên qua bia gỗ thì đạn có vận tốc 100 m/s. Lực cản của tấm bia gỗ tác dụng lên viên đạn là?
Câu 2 :
Trung tâm bồi dưỡng kiến thức Hà Nội tổ chức một cuộc thi cho các học viên chạy. Có một học viên có trọng lượng là 700 N chạy đều hết quãng đường 600 m trong 50 s. Động năng của học viên đó là bao nhiêu? Lấy g = 10 m/s2
Câu 3 :
Cho một vật có khối lượng 500 g đang chuyển động với vận tốc ban đầu là 18 km/h. Tác dụng của một lực F thì vật đạt vận tốc 36 km/h. Công của lực tác dụng là bao nhiêu? Lấy g = 10 m/s2
Câu 4 :
Khi khối lượng giảm đi bốn lần nhưng vận tốc của vật tăng gấp đôi thì động năng của vật sẽ:
Câu 5 :
Lực nào sau đây không làm vật thay đổi động năng?
Câu 6 :
Động năng của vật tăng khi:
Câu 7 :
Một vật đang đứng yên thì tác dụng một lực F không đổi làm vật bắt đầu chuyển động và đạt được vận tốc v sau khi kho đi được quãng đường s. Nếu tăng lực tác dụng lên 9 lần thì vận tốc vật sẽ đạt được bao nhiêu khi cùng đi quãng đường s.
Câu 8 :
Một ô tô có khối lượng 1500 kg đang chuyển động với vận tốc 54 km/h. Tài xế tắt máy và hãm phanh, ô tô đi thêm 50 m thì dừng lại. Lực ma sát có độ lớn là bao nhiêu?
Câu 9 :
Một người có khối lượng 60 kg đứng trên mặt đất và cạnh một cái giếng nước, lấy g = 10 m/s2 . Thế năng của người tại vị trí A cách mặt đất 3 m về phía trên và tại đáy giếng B cách mặt đất 5 m với thế năng tại mặt đất lần lượt là bao nhiêu?
Câu 10 :
Một người có khối lượng 60 kg đứng trên mặt đất và cạnh một cái giếng nước, lấy g = 10 m/s2 . Công của trọng lực khi người di chuyển từ đáy giếng lên độ cao 3 m so với mặt đất là bao nhiêu với gốc thế năng tại mặt đất.
Câu 11 :
Một học sinh lớp 10 trong giờ học môn Vật Lí làm thí nghiệm thả một quả cầu có khối lượng 250 g từ độ cao 1,5 m so với mặt đất. Hỏi khi vật đạt vận tốc 18 km/h thì vật đang ở độ cao bao nhiêu so với mặt đất. Chọn vị trí được thả làm gốc thế năng. Lấy g = 10 m/s2
Câu 12 :
Một học sinh của trung tâm bồi dưỡng kiến thức Hà Nội thả một vật rơi tự do có khối lượng 500 g từ độ cao 45 m so với mặt đất, bỏ qua ma sát với không khí. Thế năng của vật tại giây thứ hai so với mặt đất là bao nhiêu? Cho g = 10 m/s2
Câu 13 :
Một học sinh hạ 1 quyển sách khối lượng m xuống dưới1 khoảng h với vận tốc không đổi v. Công đã thực hiện bởi trọng lực là:
Câu 14 :
Một học sinh hạ 1 quyển sách khối lượng m xuống dưới 1 khoảng h với vận tốc không đổi v. Công của tay bạn học sinh đó là
Câu 15 :
Một bạn học sinh hạ 1 quyển sách khối lượng m xuống dưới 1 khoảng h với vận tốc không đổi v. Công của hợp lực tác dụng vào quyển sách là:
Câu 16 :
Một vật khối lượng 2 kg có thế năng 80 J đối với mặt đất. Lấy g = 10 m/s2 . Khi đó vật ở độ cao
Câu 17 :
Khi một vật rơi từ độ cao z, với cùng một vận tốc đầu, bay xuống đất theo những con đường khác nhau (bỏ qua ma sát). Chọn câu sai
Câu 18 :
Cho rằng bạn muốn đi lên dốc đúng bằng xe đạp leo núi. Bản chỉ dẫn có 1 đường, đường thứ nhất gấp 2 lần chiều dài đường kia. Bỏ qua ma sát, nghĩa là xem như bạn chỉ cần “chống lại lực hấp dẫn”. So sánh lực trung bình của bạn sinh ra khi đi theo đường ngắn và lực trung bình khi đi theo đường dài là:
Câu 19 :
Cho một vật có khối lượng 200 g đang ở độ cao 10 m so với mặt đất, sau đó thả vật cho rơi tự do. Tìm công của trọng lực và vận tốc của vật rơi đến độ cao 6 m.
Câu 20 :
Một ô tô khối lượng m đang chuyển động với vận tốc \(\vec v\)thì tài xế tắt máy. Công của lực ma sát tác dụng lên xe làm xe dừng lại là:
Câu 21 :
Một vật có khối lượng m = 400 g và động năng 20 J. Khi đó vận tốc của vật là:
Câu 22 :
Một người có khối lượng $50 kg$, ngồi trên ô tô đang chuyển động với vận tốc $72 km/h$. Động năng của người đó với ô tô là:
Câu 23 :
Nếu khối lượng của vật giảm 4 lần và vận tốc tăng lên 2 lần, thì động năng của vật sẽ:
Câu 24 :
Tìm câu sai.
Câu 25 :
Tìm câu sai. Động năng của một vật không đổi khi
Câu 26 :
Có hai vật $m_1$ và $m_2$ cùng khối lượng $2m$, chuyển động thẳng đều cùng chiều, vận tốc $m_1$ so với $m_2$ có độ lớn bằng $v$, vận tốc của $m_2$ so với người quan sát đứng yên trên mặt đất cũng có độ lớn bằng $v$. Kết luận nào sau đây là sai?
Câu 27 :
Một chiếc xe khối lượng $m$ có một động cơ có công suất $P$. Thời gian ngắn nhất để xe tăng tốc từ đứng yên đến vận tốc $v$ bằng:
Câu 28 :
Một máy bay vận tải đang bay với vận tốc $180 km/h$ thì ném ra phía sau một thùng hàng khối lượng $10 kg$ với vận tốc $5 m/s$ đối với máy bay. Động năng của thùng hàng ngay khi ném đối với người đứng trên mặt đất là:
Câu 29 :
Một viên đạn khối lượng $m= 100 g$ đang bay ngang với vận tốc $25 m/s$ thì xuyên vào một tấm ván mỏng dày $5 cm$ theo phương vuông góc với tấm vá. Ngay sau khi ra khỏi tấm ván vận tốc của viên đạn bằng $15 m/s$. Độ lớn của lực cản trung bình tấm ván tác dụng lên viên đạn bằng:
Câu 30 :
Bao lâu sau khi bắt đầu rơi tự do một vật có khối lượng $100 g$ có động năng bằng $15 J$ ? Lấy $g = 10 m/s^2$.
Câu 31 :
Từ mặt đất, một vật được ném lên thẳng đứng với vận tốc ban đầu $10 m/s$. Bỏ qua sức cản không khí. Cho $g = 10 m/s^2$. Vị trí cao nhất mà vật lên được cách mặt đất một khoảng bằng:
Câu 32 :
Một vật có khối lượng 0,2 kg được ném thẳng đứng từ mặt đất với vận tốc 10 m/s. Lấy g = 10 m/s2. Bỏ qua sức cản. Khi vật đi được quãng đường 8 m thì động năng của vật có giá trị bằng
Câu 33 :
Một búa máy khối lượng $900 kg$ rơi từ độ cao $2 m$ vào một cái cọc khối lượng $100 kg$. Va chạm giữa búa và cọc là va chạm mềm. Cho $g = 10 m/s^2$. Động năng của hệ (búa + cọc) sau va chạm là:
Câu 34 :
Động năng được tính bằng biểu thức:
Câu 35 :
Động năng là đại lượng:
Câu 36 :
Đơn vị nào sau đây không phải đơn vị của động năng?
Câu 37 :
Công thức nào sau đây thể hiện mối liên hệ giữa động lượng và động năng?
Câu 38 :
Một vật bắt đầu trượt không ma sát trên mặt phẳng nghiêng nghiêng góc α và từ độ cao h. Khi xuống đến chân mặt phẳng nghiêng thì vật có vận tốc là\(v\). Người ta tăng góc nghiêng lên thành 2α và cũng thả vật trượt từ độ cao h. Vận tốc của vật khi trượt tới chân mặt phẳng nghiêng là:
Câu 39 :
Một vật khối lượng m = 2 kg đang nằm yên trên một mặt phẳng ngang không ma sát. Dưới tác dụng của lực nằm ngang 9 N, vật chuyển động và đi được 9 m. Tính vận tốc của vật ở cuối chuyển dời ấy.
Câu 40 :
Một ô tô có khối lượng 1600kg đang chạy với vận tốc 54km/h thì người lái nhìn thấy một vật cản trước mặt cách một khoảng 16m. Người đó tắt máy và hãm phanh khẩn cấp. Giả sử lực hãm ô tô là không đổi và bằng \(1,{2.10^4}N\). Hỏi quãng đường xe đi được từ khi hãm phanh đến khi dừng lại là bao nhiêu? Xe có kịp dừng tránh đâm vào vật cản không?
Câu 41 :
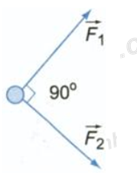
Trên mặt phẳng nhẵn nằm ngang, vật chịu tác dụng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) trong mặt phẳng và có phương vuông góc với nhau. Khi vật dịch chuyển được 5m từ trạng thái nghỉ, động năng của vật bằng bao nhiêu? Biết F1 = F2 = 10N
Câu 42 :
Một ô tô tải (xe 1) khối lượng 6 tấn và một ô tô con (xe 2) khối lượng 1200kg chuyển động cùng chiều trên đường, chiếc trước chiếc sau với cùng vận tốc không đổi 72km/h. Động năng của mỗi ô tô là:
Câu 43 :
Động năng của 1 vật thay đổi ra sao nếu khối lượng của vật không đổi nhưng vận tốc tăng 2 lần?
Câu 44 :
Biểu thức nào sau đây xác định thế năng hấp dẫn của một vật có khối lượng m, ở độ cao h so với mặt đất. Chọn gốc thế năng ở mặt đất
Câu 45 :
Chọn phương án sai. Khi một vật từ độ cao z, với cùng vận tốc ban đầu, bay xuống đất theo những con đường khác nhau thì:
Câu 46 :
Một vật được ném thẳng đứng từ dưới lên cao. Trong quá trình chuyển động của vật thì:
Câu 47 :
Một lò xo có độ cứng k, bị kéo giãn ra một đoạn x. Thế năng đàn hồi của lò xo được tính bằng biểu thức:
Câu 48 :
Thế năng hấp dẫn là đại lượng:
Câu 49 :
Phát biểu nào sau đây sai: Thế năng hấp dẫn và thế năng đàn hồi:
Câu 50 :
Một vật khối lượng m gắn vào một đầu một lò xo đàn hồi có độ cứng k, đầu kia của lò xo cố định. Khi lò xo bị nén một đoạn \(\Delta l\left( {\Delta l < 0} \right)\) thì thế năng đàn hồi bằng bao nhiêu?
Câu 51 :
Dưới tác dụng của lực bằng \(5N\) lò xo bị giãn ra \(2 cm\). Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là:
Câu 52 :
Đại lượng vật lí nào sau đây phụ thuộc vào vị trí của vật trong trọng trường?
Câu 53 :
Xét một vật chuyển động thẳng biến đổi đều theo phương nằm ngang. Đại lượng nào sau đây không đổi?
Câu 54 :
Một lò xo bị nén 5 cm. Biết độ cứng của lò xo k = 100N/m, thế năng đàn hồi của lò xo là:
Câu 55 :
Một lò xo bị giãn 4cm, có thế năng đàn hồi 0,2 J. Độ cứng của lò xo là:
Câu 56 :
Hai vật có khối lượng là m và $2m$ đặt ở hai độ cao lần lượt là $2h$ và $h$. Thế năng hấp dẫn của vật thứ nhất so với vật thứ hai là:
Câu 57 :
Một thang máy có khối lượng 1 tấn chuyển động từ tầng cao nhất cách mặt đất 100m xuống tầng thứ 10 cách mặt đất 40m. Nếu chọn gốc thế năng tại tầng 10, lấy g = 9,8m/s2. Thế năng của thang máy ở tầng cao nhất là:
Câu 58 :
Một buồng cáp treo chở người có khối lượng tổng cộng \(800kg\) đi từ vị trí xuất phát cách mặt đất \(10m\) tới một trạm dừng trên núi ở độ cao \(550m\) sau đó lại tiếp tục tới một trạm khác cao hơn. Lấy \(g = 10m/{s^2}\). Công do trọng lực thực hiện khi buồng cáp treo di chuyển từ vị trí xuất phát tới trạm dừng thứ nhất là:
Câu 59 :
Một vật có khối lượng \(2kg\) được đặt ở vị trí trong trọng trường và có thế năng tại đó \({{\rm{W}}_{{t_1}}} = 500J\). Thả vật rơi tự do đến mặt đất có thế năng \({{\rm{W}}_{{t_2}}} = - 900J\). Lấy \(g = 10m/{s^2}\). So với mặt đất vật đã rơi từ độ cao
Câu 60 :
Cho một lò xo nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực F = 4N kéo lò xo cũng theo phương ngang, ta thấy nó dãn ra được 2cm. Tìm độ cứng của lò xo và thế năng đàn hồi của lò xo khi nó dãn ra được 3cm là:
Câu 61 :
Một cần cẩu nâng một contenơ có khối lượng 3200kg từ mặt đất lên độ cao 3m (tính theo di chuyển của trọng tâm của contenơ), sau đó đổi hướng và hạ nó xuống sàn một ô tô tải ở độ cao cách mặt đất 1,5m. Lấy g = 10m/s2. Thế năng của contenơ trong trọng trường khi nó ở độ cao 3m và công của lực phát động (lực căng của dây cáp) để nâng nó lên độ cao này là bao nhiêu, coi chuyển động là đều.
Câu 62 :
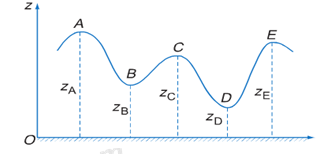
Trong công viên giải trí, một xe có khối lượng m = 100kg chạy trên đường ray có mặt cắt như hình vẽ. Độ cao của các điểm A, B, C, D, E được tính đối với mặt đất và có các giá trị: \({z_A}\; = 20m;{z_B}\; = 10m;{z_C}\; = 15m;{z_D}\; = 5m;{z_E}\; = 18m\). Lấy g = 10m/s2. Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến B; từ B đến C; từ A đến D; từ A đến E có giá trị lần lượt là:
Câu 63 :
Một lò xo có độ cứng \(k = 40N/m\), chọn mốc thế năng ở vị trí lò xo không biến dạng thì khi lò xo dãn \(3cm\) thế năng đàn hồi của lò xo bằng
Lời giải và đáp án
Câu 1 :
Vận động viên Hoàng Xuân Vinh bắn một viên đạn có khối lượng 100 g bay ngang với vận tốc 300 m/s xuyên qua tấm bia bằng gỗ dày 5 cm. Sau khi xuyên qua bia gỗ thì đạn có vận tốc 100 m/s. Lực cản của tấm bia gỗ tác dụng lên viên đạn là?
Đáp án : D Phương pháp giải :
Định lí biến thiên động năng: \(A = {F_c}.s = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\) Lời giải chi tiết :
Áp dụng định lí biến thiên động năng, ta có: \(\begin{array}{l}A = {F_c}.s = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\\ \Rightarrow {F_c} = \frac{{\frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2}}{s} = \frac{{\frac{1}{2}.0,1({{100}^2} - {{300}^2})}}{{0,05}} = - 80000(N)\end{array}\)
Câu 2 :
Trung tâm bồi dưỡng kiến thức Hà Nội tổ chức một cuộc thi cho các học viên chạy. Có một học viên có trọng lượng là 700 N chạy đều hết quãng đường 600 m trong 50 s. Động năng của học viên đó là bao nhiêu? Lấy g = 10 m/s2
Đáp án : B Phương pháp giải :
Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Theo bài ta có: P = m.g => m = P/g = 700/10 = 70 (kg) Tốc độ của vận động viên là: \(v = \frac{s}{t} = \frac{{600}}{{50}} = 12(m/s)\) => Động năng của học viên đó là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}{.70.12^2} = 5040(J)\)
Câu 3 :
Cho một vật có khối lượng 500 g đang chuyển động với vận tốc ban đầu là 18 km/h. Tác dụng của một lực F thì vật đạt vận tốc 36 km/h. Công của lực tác dụng là bao nhiêu? Lấy g = 10 m/s2
Đáp án : C Phương pháp giải :
Định lí biến thiên động năng: \(A = {F_c}.s = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\) Lời giải chi tiết :
Ta có: m = 500 g = 0,5 kg; v1 = 18 km/h = 5 m/s; v2 = 36 km/h = 10 m/s Công của lực tác dụng là: \(A = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 = \frac{1}{2}.0,5.({10^2} - {5^2}) = 18,75(J)\)
Câu 4 :
Khi khối lượng giảm đi bốn lần nhưng vận tốc của vật tăng gấp đôi thì động năng của vật sẽ:
Đáp án : A Phương pháp giải :
Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có \({m_2} = \frac{{{m_1}}}{4};{v_2} = 2{v_1}\) \(\begin{array}{l}\frac{{{W_{d2}}}}{{{W_{d1}}}} = \frac{{\frac{1}{2}{m_2}v_2^2}}{{\frac{1}{2}{m_1}v_1^2}} = \frac{{\frac{{{m_1}}}{4}.{{(2{v_1})}^2}}}{{{m_1}.v_1^2}} = 1\\ \Rightarrow {W_{d2}} = {W_{d1}}\end{array}\)
Câu 5 :
Lực nào sau đây không làm vật thay đổi động năng?
Đáp án : B Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Vì những vật có lực vuông góc với phương chuyển động thì không sinh công
Câu 6 :
Động năng của vật tăng khi:
Đáp án : D Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Động năng của vật tăng khi ngoại lực tác dụng lên vật sinh công dương
Câu 7 :
Một vật đang đứng yên thì tác dụng một lực F không đổi làm vật bắt đầu chuyển động và đạt được vận tốc v sau khi kho đi được quãng đường s. Nếu tăng lực tác dụng lên 9 lần thì vận tốc vật sẽ đạt được bao nhiêu khi cùng đi quãng đường s.
Đáp án : B Phương pháp giải :
Định lí động năng: \(\frac{1}{2}m{v^2} = F.s \Rightarrow {v^2} = 2.\frac{{F.s}}{m}\) Lời giải chi tiết :
Theo định lí động năng thì F tăng lên 9 lần thì v tăng lên 3 lần
Câu 8 :
Một ô tô có khối lượng 1500 kg đang chuyển động với vận tốc 54 km/h. Tài xế tắt máy và hãm phanh, ô tô đi thêm 50 m thì dừng lại. Lực ma sát có độ lớn là bao nhiêu?
Đáp án : B Phương pháp giải :
Định lí động năng: \(\frac{1}{2}m{v^2} = F.s\) Lời giải chi tiết :
Đổi 54 km/h = 15 m/s Ta có: \(\frac{1}{2}m{v^2} = F.s \Rightarrow F = \frac{{m{v^2}}}{{2s}} = \frac{{{{1500.15}^2}}}{{2.50}} = 3375(N)\)
Câu 9 :
Một người có khối lượng 60 kg đứng trên mặt đất và cạnh một cái giếng nước, lấy g = 10 m/s2 . Thế năng của người tại vị trí A cách mặt đất 3 m về phía trên và tại đáy giếng B cách mặt đất 5 m với thế năng tại mặt đất lần lượt là bao nhiêu?
Đáp án : C Phương pháp giải :
Công thức tính thế năng: W = m.g.z Trong đó: + m: khối lượng của vật (kg) + g: gia tốc trọng trường (m/s2 ) + z: độ cao so với mốc (m) Lời giải chi tiết :
Mốc thế năng tại mặt đất nên zA = 3 m; zB = -5 m Thế năng tại A là: WA = m.g.zA = 60.10.3 = 1800 (J) Thế năng tại B là: WB = m.g.zB = 60.10.(-5) = -3000 (J)
Câu 10 :
Một người có khối lượng 60 kg đứng trên mặt đất và cạnh một cái giếng nước, lấy g = 10 m/s2 . Công của trọng lực khi người di chuyển từ đáy giếng lên độ cao 3 m so với mặt đất là bao nhiêu với gốc thế năng tại mặt đất.
Đáp án : D Phương pháp giải :
Định lí biến thiên thế năng: A = WtB – WtA = m.g.(zB – zA ) Lời giải chi tiết :
Thế năng tại A cách mặt đất 3 m là: WA = m.g.zA = 60.10.3 = 1800 (J) Thế năng tại B phía dưới đáy giếng cách mặt đất 5 m là: WB = m.g.zB = 60.10.(-5) = -3000 (J) => Công của trọng lực khi di chuyển từ đáy giếng lên vị trí A cách mặt đất 3 m là: A = WtB – WtA = -3000 – 1800 = -4800 (J)
Câu 11 :
Một học sinh lớp 10 trong giờ học môn Vật Lí làm thí nghiệm thả một quả cầu có khối lượng 250 g từ độ cao 1,5 m so với mặt đất. Hỏi khi vật đạt vận tốc 18 km/h thì vật đang ở độ cao bao nhiêu so với mặt đất. Chọn vị trí được thả làm gốc thế năng. Lấy g = 10 m/s2
Đáp án : A Phương pháp giải :
Định lí biến thiên thế năng: A = WtB – WtA = m.g.(zB – zA ) Lời giải chi tiết :
Ta có v = 18 km/h = 5 m/s Chọn mốc thế năng tại vị trí thả vật Áp dụng định lí động năng: \(A = \frac{1}{2}.m{v^2} = \frac{1}{2}.0,{25.5^2} = 3,125(J)\) Định lí biến thiên thế năng: A = -Wt = -mgz \( \Rightarrow z = \frac{{ - A}}{{mg}} = \frac{{ - 3,125}}{{0,25.10}} = - 1,25(m)\)( vật chuyển động ngược chiều dương, cách nơi thả vật 1,25 m) => Vật cách mặt đất 1 khoảng là: 1,5 – 1,25 = 0,25 m
Câu 12 :
Một học sinh của trung tâm bồi dưỡng kiến thức Hà Nội thả một vật rơi tự do có khối lượng 500 g từ độ cao 45 m so với mặt đất, bỏ qua ma sát với không khí. Thế năng của vật tại giây thứ hai so với mặt đất là bao nhiêu? Cho g = 10 m/s2
Đáp án : B Phương pháp giải :
Công thức rơi tự do: \(s = \frac{1}{2}g{t^2}\) Công thức tính thế năng: Wt = m.g.z Lời giải chi tiết :
Quãng đường chuyển động của vật sau 2 giây là: \(s = \frac{1}{2}g{t^2} = \frac{1}{2}{.10.2^2} = 20(m)\) => Vật cách mặt đất: z = 45 – 20 = 25 (m) Thế năng của vật là: Wt = m.g.z = 0,5.10.25 = 125 (J)
Câu 13 :
Một học sinh hạ 1 quyển sách khối lượng m xuống dưới1 khoảng h với vận tốc không đổi v. Công đã thực hiện bởi trọng lực là:
Đáp án : A Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Công đã thực hiện bởi trọng lực là công dương
Câu 14 :
Một học sinh hạ 1 quyển sách khối lượng m xuống dưới 1 khoảng h với vận tốc không đổi v. Công của tay bạn học sinh đó là
Đáp án : B Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Công của tay bạn học sinh đó là công âm
Câu 15 :
Một bạn học sinh hạ 1 quyển sách khối lượng m xuống dưới 1 khoảng h với vận tốc không đổi v. Công của hợp lực tác dụng vào quyển sách là:
Đáp án : C Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Công của hợp lực tác dụng vào quyển sách bằng 0
Câu 16 :
Một vật khối lượng 2 kg có thế năng 80 J đối với mặt đất. Lấy g = 10 m/s2 . Khi đó vật ở độ cao
Đáp án : A Phương pháp giải :
Biểu thức tính thế năng: W = mgh Lời giải chi tiết :
Từ biểu thức tính thế năng: W = mgh => \(h = \frac{W}{{mg}} = \frac{{80}}{{2.10}} = 4(m)\)
Câu 17 :
Khi một vật rơi từ độ cao z, với cùng một vận tốc đầu, bay xuống đất theo những con đường khác nhau (bỏ qua ma sát). Chọn câu sai
Đáp án : B Phương pháp giải :
Vận dụng kiến thức đã học Lời giải chi tiết :
Thế năng không phụ thuộc vào hình dạng của đường đi, chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối => khi vật rơi từ độ cao z, với cùng một vận tốc đầu thì gia tốc bằng nhau, công của trọng lực bằng nahu, độ lớn chạm đất bằng nhau
Câu 18 :
Cho rằng bạn muốn đi lên dốc đúng bằng xe đạp leo núi. Bản chỉ dẫn có 1 đường, đường thứ nhất gấp 2 lần chiều dài đường kia. Bỏ qua ma sát, nghĩa là xem như bạn chỉ cần “chống lại lực hấp dẫn”. So sánh lực trung bình của bạn sinh ra khi đi theo đường ngắn và lực trung bình khi đi theo đường dài là:
Đáp án : C Phương pháp giải :
Định lí biến thiên thế năng: A = F.s = Wt Lời giải chi tiết :
Ta có: F.s = mgh => \(F = \frac{{mgh}}{s}\) => F tỉ lệ nghịch với quãng đường
Câu 19 :
Cho một vật có khối lượng 200 g đang ở độ cao 10 m so với mặt đất, sau đó thả vật cho rơi tự do. Tìm công của trọng lực và vận tốc của vật rơi đến độ cao 6 m.
Đáp án : A Phương pháp giải :
Định lí động năng: \(A = \frac{1}{2}m{v^2}\) Định lí thế năng: A = mgz1 – mgz2 Lời giải chi tiết :
Theo độ thay đổi thế năng: A = mgz1 – mgz2 = 0,2.10.(10-6) = 8 (J) Theo định lí động năng: \(A = \frac{1}{2}m{v^2} \Rightarrow v = \sqrt {\frac{{2A}}{m}} = \sqrt {\frac{{2.4}}{{0,2}}} = 2\sqrt {10} (m/s)\)
Câu 20 :
Một ô tô khối lượng m đang chuyển động với vận tốc \(\vec v\)thì tài xế tắt máy. Công của lực ma sát tác dụng lên xe làm xe dừng lại là:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Động năng của ô tô trước khi tắt máy là: ${W_d} = \frac{{m{v^2}}}{2}$ Động năng của ô tô sau khi dừng lại là: \(W{'_d} = {\text{ }}0\) Áp dụng định lí biến thiên động năng ta có: \(A = 0 - \frac{{m{v^2}}}{2} = - \frac{{m{v^2}}}{2}\).
Câu 21 :
Một vật có khối lượng m = 400 g và động năng 20 J. Khi đó vận tốc của vật là:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Từ công thức tính động năng ta có: \({W_d} = \frac{1}{2}m{v^2} \Rightarrow v = \sqrt {\frac{{2.{W_d}}}{m}} = \sqrt {\frac{{2.20}}{{0,4}}} = 10m/s = 36km/h\)
Câu 22 :
Một người có khối lượng $50 kg$, ngồi trên ô tô đang chuyển động với vận tốc $72 km/h$. Động năng của người đó với ô tô là:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có, vận tốc của người so với ô – tô là: \(v = 0m/s\) (do người đang ngồi trên ô-tô) => Động năng của người so với ô-tô là: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = 0J\) Chú ý
Đề bài đang hỏi tính động năng của người đó với ô-tô chứ không phải của người đó với mặt đất + Vận tốc của người so với mặt đất: \(v = 72km/h = 20m/s\) + Vận tốc của người so với xe: \(v = 0m/s\)
Câu 23 :
Nếu khối lượng của vật giảm 4 lần và vận tốc tăng lên 2 lần, thì động năng của vật sẽ:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Công thức tính động năng: Wđ =\(\frac{1}{2}m{v^2}\). (*) Khi khối lượng giảm 4 lần thì: \(m' = \frac{m}{4}\), và vận tốc tăng 2 lần thì: \(v' = 2v\). Thay m’ và v’ vào công thức (*) ta có: W’đ =\(\frac{1}{2}m'{v'^2} = \frac{1}{2}\frac{m}{4}{\left( {2v} \right)^2} = \frac{1}{2}\frac{m}{4}.4.{v^2} = \frac{1}{2}m{v^2} = \)Wđ.
Câu 24 :
Tìm câu sai.
Đáp án : A Phương pháp giải :
Vận dụng lí thuyết về động lượng và động năng Lời giải chi tiết :
A - sai vì: Ta có đơn vị của: + Động lượng: \(kg.m/s\) + Động năng: \(kg.{\left( {m/s} \right)^2} = J\) B, C, D - đúng
Câu 25 :
Tìm câu sai. Động năng của một vật không đổi khi
Đáp án : D Phương pháp giải :
Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
A, B, C - đúng D - sai vì: khi vật chuyển động biến đổi đều thì vận tốc của vật thay đổi => động năng cũng thay đổi do động năng tỉ lệ thuận với bình phương vận tốc.
Câu 26 :
Có hai vật $m_1$ và $m_2$ cùng khối lượng $2m$, chuyển động thẳng đều cùng chiều, vận tốc $m_1$ so với $m_2$ có độ lớn bằng $v$, vận tốc của $m_2$ so với người quan sát đứng yên trên mặt đất cũng có độ lớn bằng $v$. Kết luận nào sau đây là sai?
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) Lời giải chi tiết :
Trong hệ quy chiếu gắn với quan sát, vật $m_1= 2 m$ có vận tốc bằng $2v$ nên động năng của vật là: \({{\rm{W}}_d} = \dfrac{{{m_1}{{\left( {2v} \right)}^2}}}{2} = \dfrac{{8m{v^2}}}{2} = 4m{v^2}\) => Phương án C - sai
Câu 27 :
Một chiếc xe khối lượng $m$ có một động cơ có công suất $P$. Thời gian ngắn nhất để xe tăng tốc từ đứng yên đến vận tốc $v$ bằng:
Đáp án : C Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) + Vận dụng biểu thức độ biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = A\) + Vận dụng biểu thức tính công suất: \(P = \dfrac{A}{t}\) Lời giải chi tiết :
Độ biến thiên động năng của vật bằng công của động cơ thực hiện trong quá trình đó \(\dfrac{{m{v^2}}}{2} - 0 = A= Pt = > t = \dfrac{m{v^2}}{2P}\)
Câu 28 :
Một máy bay vận tải đang bay với vận tốc $180 km/h$ thì ném ra phía sau một thùng hàng khối lượng $10 kg$ với vận tốc $5 m/s$ đối với máy bay. Động năng của thùng hàng ngay khi ném đối với người đứng trên mặt đất là:
Đáp án : C Phương pháp giải :
Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) Lời giải chi tiết :
Do thùng hàng được ném ra phía sau ngược chiều bay của máy bay nên theo công thức cộng vận tốc, vận tốc của thùng hàng đối với người đứng trên mặt đất bằng $50 – 5 = 45 m/s$. Do đó, động năng của thùng hàng đối với người đứng trên mặt đất là: \({{\rm{W}}_đ} = \frac{{{{10.45}^2}}}{2} = 10125J\)
Câu 29 :
Một viên đạn khối lượng $m= 100 g$ đang bay ngang với vận tốc $25 m/s$ thì xuyên vào một tấm ván mỏng dày $5 cm$ theo phương vuông góc với tấm vá. Ngay sau khi ra khỏi tấm ván vận tốc của viên đạn bằng $15 m/s$. Độ lớn của lực cản trung bình tấm ván tác dụng lên viên đạn bằng:
Đáp án : D Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_đ} = \frac{1}{2}m{v^2}\) + Vận dụng định lí biến thiên động năng: \(\Delta {{\rm{W}}_đ} = {A_{ng}}\) Lời giải chi tiết :
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng: \(\frac{{m{v_2}^2}}{2} - \frac{{m{v_1}^2}}{2} = - {F_c}s = > {F_c} = \frac{{-m\left( {{v_2}^2 - {v_1}^2} \right)}}{{2s}} = \frac{{ - 0,1\left( {{{15}^2} - {{25}^2}} \right)}}{{2.0,05}} = -400\,N\)
Câu 30 :
Bao lâu sau khi bắt đầu rơi tự do một vật có khối lượng $100 g$ có động năng bằng $15 J$ ? Lấy $g = 10 m/s^2$.
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_đ} = \frac{1}{2}m{v^2}\) + Vận dụng định lí biến thiên động năng: \(\Delta {{\rm{W}}_đ} = {A_{ng}}\) Lời giải chi tiết :
Do trọng lực sinh công phát động trong quá trình vật rơi tự do nên. \({{\rm{W}}_d} - 0 = mgh = mg\frac{{gt^2}}{2} = > t = \sqrt {\frac{{2{W_d}}}{{m{g^2}}}} = \sqrt {\frac{{2.15}}{{0,{{1.10}^2}}}} = \sqrt 3 \,s\)
Câu 31 :
Từ mặt đất, một vật được ném lên thẳng đứng với vận tốc ban đầu $10 m/s$. Bỏ qua sức cản không khí. Cho $g = 10 m/s^2$. Vị trí cao nhất mà vật lên được cách mặt đất một khoảng bằng:
Đáp án : D Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\) + Vận dụng định lí biến thiên động năng: \(\Delta {{\rm{W}}_d} = {A_{ng}}\) Lời giải chi tiết :
Khi vật lên đến vị trí cao nhất thì vận tốc bằng 0. Trong quá trinh vật chuyển động hướng lên thì trọng lực sinh công âm \(0 - \dfrac{{m{v^2}}}{2} = - mgh = > h = \dfrac{{{v^2}}}{{2g}} = \dfrac{{{{10}^2}}}{{2.10}} = 5m\)
Câu 32 :
Một vật có khối lượng 0,2 kg được ném thẳng đứng từ mặt đất với vận tốc 10 m/s. Lấy g = 10 m/s2. Bỏ qua sức cản. Khi vật đi được quãng đường 8 m thì động năng của vật có giá trị bằng
Đáp án : D Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_đ} = \frac{1}{2}m{v^2}\) + Vận dụng định lí biến thiên động năng: \(\Delta {{\rm{W}}_đ} = {A_{ng}}\) Lời giải chi tiết :
Vị trí cao nhất lên tới \(h = \frac{{{v^2}}}{{2g}} = 5m < s = 8m\) Vậy khi vật đi được quãng đường 8 m tức là trong quá trình rơi tự do trở lại, chuyển động rơi này có vận tốc ban đầu bằng 0 và trọng lực lại sinh công dương nên wđ' - 0 = mg(s – h) = 0,2.10(8 – 5) = 6 J.
Câu 33 :
Một búa máy khối lượng $900 kg$ rơi từ độ cao $2 m$ vào một cái cọc khối lượng $100 kg$. Va chạm giữa búa và cọc là va chạm mềm. Cho $g = 10 m/s^2$. Động năng của hệ (búa + cọc) sau va chạm là:
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức tính động năng : \({{\rm{W}}_đ} = \frac{1}{2}m{v^2}\) + Vận dụng định lí biến thiên động năng: \(\Delta {{\rm{W}}_đ} = {A_{ng}}\) Lời giải chi tiết :
Áp dụng định lí biến thiên động năng, vận tốc của búa ngay trước khi va chạm mềm với cọc là \(\dfrac{{{m_b}{v_b}^2}}{2} - 0 = {m_b}gh = > {v_b} = \sqrt {2gh} \) Khi va chạm giữa búa và cọc là va chạm mềm thì theo định luật bảo toàn động lượng \({m_b}{v_b} + {m_c}.0 = \left( {{m_b} + {m_c}} \right)v = > v = \dfrac{{{m_b}\sqrt {2gh} }}{{{m_b} + {m_c}}}\) Vậy động năng của hệ búa và cọc sau va chạm là: \({{\rm{W}}_đ} = \dfrac{{\left( {{m_b} + {m_c}} \right){v^2}}}{2} = \dfrac{{{m_b}^2gh}}{{{m_b} + {m_c}}} = \dfrac{{{{900}^2}.10.2}}{{900 + 100}} = 16200J\)
Câu 34 :
Động năng được tính bằng biểu thức:
Đáp án : C Lời giải chi tiết :
Biểu thức tính động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
Câu 35 :
Động năng là đại lượng:
Đáp án : A Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) => Động năng là đại lượng vô hướng, luôn dương hoặc bằng không
Câu 36 :
Đơn vị nào sau đây không phải đơn vị của động năng?
Đáp án : D Phương pháp giải :
Vận dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) và đơn vị của các đại lượng Lời giải chi tiết :
Ta có, động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) Các đơn vị của động năng: \(J = kg.{m^2}/{s^2} = N.m\) (do có \(kg.m/{s^2} = N\) ) => Phương án D: \(N.s\) không phải đơn vị của động năng
Câu 37 :
Công thức nào sau đây thể hiện mối liên hệ giữa động lượng và động năng?
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức tính động lượng : \(p = mv\) + Vận dụng biểu thức tính động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có : + Động lượng : \(p = mv\) + Động năng : \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) => \({{\rm{W}}_{\rm{d}}} = \dfrac{{{p^2}}}{{2m}}\)
Câu 38 :
Một vật bắt đầu trượt không ma sát trên mặt phẳng nghiêng nghiêng góc α và từ độ cao h. Khi xuống đến chân mặt phẳng nghiêng thì vật có vận tốc là\(v\). Người ta tăng góc nghiêng lên thành 2α và cũng thả vật trượt từ độ cao h. Vận tốc của vật khi trượt tới chân mặt phẳng nghiêng là:
Đáp án : B Phương pháp giải :
+ Áp dụng định lí biến thiên động năng: \(A = {{\rm{W}}_{d2}} - {{\rm{W}}_{d1}} = \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2\) + Khi vật chuyển động trong trọng trường từ vị trí M đến vị trí N thì công của trọng lực của vật có giá trị bằng hiệu thế năng trọng trường tại M và tại N: \({A_{\overrightarrow P }} = {{\rm{W}}_{tM}} - {{\rm{W}}_{tN}}\) Lời giải chi tiết :
Áp dụng định lí biến thiên động năng ta có: \({{\rm{W}}_{dB}} - {{\rm{W}}_{dA}} = {A_{\overrightarrow P }} + {A_{\overrightarrow Q }} \Leftrightarrow \dfrac{1}{2}mv_B^2 - \dfrac{1}{2}mv_A^2 = {A_{\overrightarrow P }}\) Mà: \(\left\{ \begin{array}{l}{A_{\overrightarrow P }} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tB}} = mg\left( {{z_A} - {z_B}} \right) = mg.AH = mg.h\\{{\rm{W}}_{dA}} = \dfrac{1}{2}mv_A^2 = 0\end{array} \right.\) \( \Rightarrow \dfrac{1}{2}mv_B^2 = mgh \Rightarrow {v_B} = \sqrt {2.gh} \) Ta thấy công thức xác định vận tốc tại chân mặt phẳng nghiêng chỉ phụ thuộc vào độ cao h mà không phụ thuộc vào góc nghiêng α. Do đó khi ta tăng góc nghiêng lên thành 2α và cũng thả vật trượt từ độ cao h thì vận tốc của vật tại chân mặt phẳng nghiêng không thay đổi.
Câu 39 :
Một vật khối lượng m = 2 kg đang nằm yên trên một mặt phẳng ngang không ma sát. Dưới tác dụng của lực nằm ngang 9 N, vật chuyển động và đi được 9 m. Tính vận tốc của vật ở cuối chuyển dời ấy.
Đáp án : C Phương pháp giải :
Định lí biến thiên động năng: \(A = \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2\) Công thức tính công: \(A = F.s.\cos \alpha \) Lời giải chi tiết :
+ Ban đầu vật nằm yên nên ta suy ra vận tốc ban đầu của vật \({v_0} = 0m/s\) + Gọi vận tốc lúc sau của vật ở cuối chuyển dời là: \(v\) Áp dụng định lí biến thiên động năng, ta có: \(A = \dfrac{1}{2}m{v^2} - \dfrac{1}{2}mv_0^2\,\,\,\,\left( * \right)\) Lại có: \(A = Fs.\cos \alpha \) Với \(\alpha = \left( {\overrightarrow F ;\overrightarrow s } \right) = 0 \Rightarrow A = F.s\) Thay vào (*) ta được: \(F.s = \dfrac{1}{2}m{v^2} - 0\, \Rightarrow v = \sqrt {\dfrac{{2F.s}}{m}} = \sqrt {\dfrac{{2.9.9}}{2}} = 9m/s\)
Câu 40 :
Một ô tô có khối lượng 1600kg đang chạy với vận tốc 54km/h thì người lái nhìn thấy một vật cản trước mặt cách một khoảng 16m. Người đó tắt máy và hãm phanh khẩn cấp. Giả sử lực hãm ô tô là không đổi và bằng \(1,{2.10^4}N\). Hỏi quãng đường xe đi được từ khi hãm phanh đến khi dừng lại là bao nhiêu? Xe có kịp dừng tránh đâm vào vật cản không?
Đáp án : A Phương pháp giải :
Định lí biến thiên động năng: \(A = \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2\) Công thức tính công: \(A = F.s.\cos \alpha \) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}m = 1600kg\\{v_0} = 55km/h = 15m/s\\v = 0\\{F_h} = 1,{2.10^4}N\end{array} \right.\) Động năng ban đầu của xe: \({{\rm{W}}_{d0}} = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}{.1600.15^2} = 180000J\) Khi xe dừng lại thì \(v = 0 \Rightarrow {{\rm{W}}_d} = 0\) Công của lực hãm:\({A_h} = {F_h}.s.\cos 180 = - 1,{2.10^4}.s\,\,\left( J \right)\) Áp dụng định lí biến thiên động năng ta có: \(\begin{array}{l}{{\rm{A}}_h}{\rm{ = }}{{\rm{W}}_d} - {{\rm{W}}_{d0}} \Leftrightarrow - 1,{2.10^4}.s = 0 - 180000\\ \Rightarrow s = \dfrac{{0 - 180000}}{{ - 1,{{2.10}^4}}} = 15m < 16m\end{array}\) Vậy xe có kịp dừng lại.
Câu 41 :
Trên mặt phẳng nhẵn nằm ngang, vật chịu tác dụng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) trong mặt phẳng và có phương vuông góc với nhau. Khi vật dịch chuyển được 5m từ trạng thái nghỉ, động năng của vật bằng bao nhiêu? Biết F1 = F2 = 10N
Đáp án : A Phương pháp giải :
Định lí biến thiên động năng: \(A = \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2\) Công thức tính công: \(A = F.s.\cos \alpha \) Lời giải chi tiết :
Hợp lực tác dụng lên vật:\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) Do \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_2}} \) nên hợp lực có độ lớn là : \(F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\) Vật chuyển động theo hướng của lực \(\overrightarrow F \)nên công của hợp lực tác dụng lên vật là : \({A_F}\; = F.s.\cos 0 = 10\sqrt 2 .5 = 50\sqrt 2 {\rm{ }}J\) Vật dịch chuyển từ trạng thái nghỉ nên \({v_0}{\rm{ = 0}} \Rightarrow {{\rm{W}}_{d0}} = 0\) Áp dụng định lí biến thiên động năng ta có: \({A_F} = {{\rm{W}}_d} - {{\rm{W}}_{d0}} \Leftrightarrow {{\rm{W}}_d} = {A_F} = 50\sqrt 2 J\)
Câu 42 :
Một ô tô tải (xe 1) khối lượng 6 tấn và một ô tô con (xe 2) khối lượng 1200kg chuyển động cùng chiều trên đường, chiếc trước chiếc sau với cùng vận tốc không đổi 72km/h. Động năng của mỗi ô tô là:
Đáp án : A Phương pháp giải :
Động năng là dạng năng lượng của một vật có được do nó đang chuyển động và được xác định theo công thức: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}{m_1} = 6T = 6000kg\\{m_2} = 1200kg\\{v_1} = {v_2} = 72km/h = 20m/s\end{array} \right.\) Động năng của mỗi ô tô là: \(\left\{ \begin{array}{l}{{\rm{W}}_{d1}} = \dfrac{1}{2}mv_1^2 = \dfrac{1}{2}{.6000.20^2} = 1\,200\,000J\\{{\rm{W}}_{d2}} = \dfrac{1}{2}mv_2^2 = \dfrac{1}{2}{.1200.20^2} = 240\,000J\end{array} \right.\)
Câu 43 :
Động năng của 1 vật thay đổi ra sao nếu khối lượng của vật không đổi nhưng vận tốc tăng 2 lần?
Đáp án : B Phương pháp giải :
Công thức tính động năng: \({W_d} = \dfrac{1}{2}m{v^2}\) Lời giải chi tiết :
Ta có: \({W_d} = \dfrac{1}{2}m{v^2} \Rightarrow {W_d} \sim {v^2}\) \( \Rightarrow \) Khi vận tốc tăng 2 lần thì động năng tăng 4 lần.
Câu 44 :
Biểu thức nào sau đây xác định thế năng hấp dẫn của một vật có khối lượng m, ở độ cao h so với mặt đất. Chọn gốc thế năng ở mặt đất
Đáp án : B Phương pháp giải :
Sử dụng biểu thức xác định thế năng đàn hồi Lời giải chi tiết :
Nếu chọn gốc thế năng là mặt đất thì công thức tính thế năng trọng trường của một vật ở độ cao h là: \({{\rm{W}}_t} = mgh\)
Câu 45 :
Chọn phương án sai. Khi một vật từ độ cao z, với cùng vận tốc ban đầu, bay xuống đất theo những con đường khác nhau thì:
Đáp án : B Phương pháp giải :
Vận dụng lý thuyết về sự rơi của các vật Lời giải chi tiết :
A, C, D – đúng B – sai vì : thời gian rơi phụ thuộc vào gia tốc rơi tự do và vận tốc ban đầu theo phương thẳng đứng. Ở đây vận tốc ban đầu như nhau nhưng đường đi khác nhau nên vận tốc ban đầu theo phương thẳng đứng khác nhau.
Câu 46 :
Một vật được ném thẳng đứng từ dưới lên cao. Trong quá trình chuyển động của vật thì:
Đáp án : D Phương pháp giải :
Vận dụng biểu thức tính thế năng và công Lời giải chi tiết :
Ta có : Khi một vật được ném lên, độ cao của vật tăng dần nên thế năng tăng. Trong quá trình chuyển động của vật từ dưới lên, trọng lực luôn hướng ngược chiều chuyển động nên nó là lực cản, do đó trọng lực sinh công âm.
Câu 47 :
Một lò xo có độ cứng k, bị kéo giãn ra một đoạn x. Thế năng đàn hồi của lò xo được tính bằng biểu thức:
Đáp án : A Phương pháp giải :
Sử dụng biểu thức tính thế năng đàn hồi Lời giải chi tiết :
Công thức tính thế năng đàn hồi của lò xo: \({{\rm{W}}_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2}\) trong đó \(\Delta l\): độ biến dạng của lò xo
Câu 48 :
Thế năng hấp dẫn là đại lượng:
Đáp án : B Phương pháp giải :
Vận dụng biểu thức tính thế năng hấp dẫn: \({{\rm{W}}_t} = mg{\rm{z}}\) Lời giải chi tiết :
Ta có, thế năng hấp dẫn là đại lượng vô hướng, có thể âm, dương hoặc bằng 0
Câu 49 :
Phát biểu nào sau đây sai: Thế năng hấp dẫn và thế năng đàn hồi:
Đáp án : D Phương pháp giải :
Vận dụng biểu định nghĩa và biểu thức về thế năng đàn hồi và thế năng hấp dẫn Lời giải chi tiết :
Thế năng đàn hồi và thế năng hấp dẫn đều là đại lượng vô hướng + Thế năng hấp dẫn có thể dương, âm hoặc bằng 0 + Thế năng đàn hồi luôn lớn hơn hoặc bằng 0 => Phương án D - sai
Câu 50 :
Một vật khối lượng m gắn vào một đầu một lò xo đàn hồi có độ cứng k, đầu kia của lò xo cố định. Khi lò xo bị nén một đoạn \(\Delta l\left( {\Delta l < 0} \right)\) thì thế năng đàn hồi bằng bao nhiêu?
Đáp án : A Phương pháp giải :
Sử dụng biểu thức tính thế năng đàn hồi Lời giải chi tiết :
Công thức tính thế năng đàn hồi của lò xo: \({{\rm{W}}_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2}\) trong đó \(\Delta l\): độ biến dạng của lò xo
Câu 51 :
Dưới tác dụng của lực bằng \(5N\) lò xo bị giãn ra \(2 cm\). Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là:
Đáp án : A Phương pháp giải :
Vận dụng biểu định luật Húc và công + Biểu thức định luật Húc: \(F=|kx|\) + Công: \(A=W_t=\dfrac{kx^2}{2}\) Lời giải chi tiết :
Theo định luật Húc: \({F_{dh}} = k.\left( {\Delta l} \right) \Rightarrow k = \dfrac{F}{{\Delta l}} = \dfrac{5}{{0,02}} = 250N/m\). Công của ngoại lực tác dụng để lò xo giãn ra \(5 cm\) là: \(A = {W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}.250.{\left( {0,05} \right)^2} = 0,3125J\)\( \approx 0,31J\).
Câu 52 :
Đại lượng vật lí nào sau đây phụ thuộc vào vị trí của vật trong trọng trường?
Đáp án : B Phương pháp giải :
Vận dụng định nghĩa về động năng, động lượng, thế năng và trọng lượng của vật Lời giải chi tiết :
Đại lượng phụ thuộc vào vị trí của vật trong trọng trường là thế năng
Câu 53 :
Xét một vật chuyển động thẳng biến đổi đều theo phương nằm ngang. Đại lượng nào sau đây không đổi?
Đáp án : C Phương pháp giải :
Vận dụng định nghĩa về động năng, động lượng, thế năng và vận tốc của vật Lời giải chi tiết :
Khi vật chuyển động theo phương ngang thì vị trí trọng trường của vật không đổi => thế năng không đổi
Câu 54 :
Một lò xo bị nén 5 cm. Biết độ cứng của lò xo k = 100N/m, thế năng đàn hồi của lò xo là:
Đáp án : D Phương pháp giải :
Sử dụng biểu thức tính thế năng đàn hồi Lời giải chi tiết :
Ta có: \({W_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2} = \frac{1}{2}100{\left( {0,05} \right)^2} = 0,125J.\)
Câu 55 :
Một lò xo bị giãn 4cm, có thế năng đàn hồi 0,2 J. Độ cứng của lò xo là:
Đáp án : B Phương pháp giải :
Sử dụng biểu thức tính thế năng đàn hồi rồi suy ra các đại lượng cần tính có trong biểu thức Lời giải chi tiết :
Ta có: \({W_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2} \Rightarrow k = \frac{{2{W_t}}}{{{{\left( {\Delta l} \right)}^2}}} = \frac{{2.0,2}}{{{{\left( {0.04} \right)}^2}}} = 250N/m\).
Câu 56 :
Hai vật có khối lượng là m và $2m$ đặt ở hai độ cao lần lượt là $2h$ và $h$. Thế năng hấp dẫn của vật thứ nhất so với vật thứ hai là:
Đáp án : C Phương pháp giải :
Sử dụng biểu thức tính thế năng trọng trường Lời giải chi tiết :
Ta có: Thế năng của vật 1 có giá trị là: \({W_{t1}} = m.g.2.h = 2mgh\) (1). Thế năng của vật 2 có giá trị là: \({W_{t2}} = 2.m.g.h = 2mgh\) (2). =>thế năng vật 1 bằng thế năng vật 2
Câu 57 :
Một thang máy có khối lượng 1 tấn chuyển động từ tầng cao nhất cách mặt đất 100m xuống tầng thứ 10 cách mặt đất 40m. Nếu chọn gốc thế năng tại tầng 10, lấy g = 9,8m/s2. Thế năng của thang máy ở tầng cao nhất là:
Đáp án : A Phương pháp giải :
Sử dụng biểu thức tính thế năng trọng trường Lời giải chi tiết :
Ta có gốc thế năng tại tầng thứ 10 nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là: z =100 – 40 = 60m. Thế năng của thang máy là: \({W_t} = mgz = 1000.9,8.60 = 588kJ\).
Câu 58 :
Một buồng cáp treo chở người có khối lượng tổng cộng \(800kg\) đi từ vị trí xuất phát cách mặt đất \(10m\) tới một trạm dừng trên núi ở độ cao \(550m\) sau đó lại tiếp tục tới một trạm khác cao hơn. Lấy \(g = 10m/{s^2}\). Công do trọng lực thực hiện khi buồng cáp treo di chuyển từ vị trí xuất phát tới trạm dừng thứ nhất là:
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính thế năng: \({{\rm{W}}_t} = mgz\) + Sử dụng biểu thức biến thiên thế năng: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = A\) Lời giải chi tiết :
Chọn mốc thế năng tại mặt đất + Tại vị trí xuất phát, cáp treo có độ cao \({z_1} = 10m\) + Tại trạm thứ nhất, cáp treo có độ cao \({z_2} = 550m\) Công của trọng lực bằng độ giảm thế năng: \(\begin{array}{l}{A_P} = {{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = mg{z_1} - mg{z_2}\\ = mg\left( {{z_1} - {z_2}} \right)\\ = 800.10\left( {10 - 550} \right)\\ = - 4320000J = - {432.10^4}J\end{array}\)
Câu 59 :
Một vật có khối lượng \(2kg\) được đặt ở vị trí trong trọng trường và có thế năng tại đó \({{\rm{W}}_{{t_1}}} = 500J\). Thả vật rơi tự do đến mặt đất có thế năng \({{\rm{W}}_{{t_2}}} = - 900J\). Lấy \(g = 10m/{s^2}\). So với mặt đất vật đã rơi từ độ cao
Đáp án : C Phương pháp giải :
+ Sử dụng biểu thức biến thiên thế năng: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = A\) + Sử dụng biểu thức tính công: \(A = Fs\cos \alpha \) Lời giải chi tiết :
Ta có: + Biến thiên thế năng chính bằng công của trọng lực: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = {A_P}\) (1) + \(\overrightarrow P \) hợp với phương rơi một góc \(\alpha = {0^0}\) Ta suy ra công của trọng lực: \({A_P} = P.h = mgh\) (2) Từ (1) và (2), ta suy ra: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = mgh\) \( \Rightarrow h = \dfrac{{{{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}}}}{{mg}} = \dfrac{{500 - \left( { - 900} \right)}}{{2.10}} = 70m\) Vậy so với mặt đất, vật đã rơi từ độ cao \(h = 70m\)
Câu 60 :
Cho một lò xo nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực F = 4N kéo lò xo cũng theo phương ngang, ta thấy nó dãn ra được 2cm. Tìm độ cứng của lò xo và thế năng đàn hồi của lò xo khi nó dãn ra được 3cm là:
Đáp án : A Phương pháp giải :
Lực đàn hồi: \({F_{dh}} = k.\left| {\Delta l} \right|\) Công thức tính thế năng đàn hồi của một lò xo ở trạng thái có biến dạng ∆l là: \({{\rm{W}}_t} = \dfrac{1}{2}{k^2}.\Delta l\) Lời giải chi tiết :
Lực đàn hồi: \({F_{dh}} = k.\left| {\Delta l} \right|\) Có: \(\left\{ \begin{array}{l}{F_{dh}} = 4N\\\Delta l = 2cm = 0,02m\end{array} \right.\) Độ cứng: \(k = \dfrac{{{F_{dh}}}}{{\left| {\Delta l} \right|}} = \dfrac{4}{{0,02}} = 200N/m\) Thế năng đàn hồi của lò xo khi nó dãn ra được 3cm là: \({{\rm{W}}_{dh}} = \dfrac{1}{2}k.\Delta l{'^2} = \dfrac{1}{2}.200.0,{03^2} = 0,09J\)
Câu 61 :
Một cần cẩu nâng một contenơ có khối lượng 3200kg từ mặt đất lên độ cao 3m (tính theo di chuyển của trọng tâm của contenơ), sau đó đổi hướng và hạ nó xuống sàn một ô tô tải ở độ cao cách mặt đất 1,5m. Lấy g = 10m/s2. Thế năng của contenơ trong trọng trường khi nó ở độ cao 3m và công của lực phát động (lực căng của dây cáp) để nâng nó lên độ cao này là bao nhiêu, coi chuyển động là đều.
Đáp án : A Phương pháp giải :
Công thức tính thế năng: \({{\rm{W}}_t} = mgz\) Liên hệ giữa biến thiên thế năng và công của trọng lực: \(A = {{\rm{W}}_{tM}} - {{\rm{W}}_{tN}} = mg.\left( {{z_M} - {z_N}} \right) = mg.\Delta z\) Lời giải chi tiết :
Chọn mốc thế năng tại mặt đất. Thế năng của contenơ trong trọng trường khi nó ở độ cao 3m là: \({{\rm{W}}_t} = mgz = 3200.10.3 = 96000J\) Coi chuyển động là đều thì công của lực phát động bằng độ lớn công cản (công của trọng lực) nên ta có: \({{\rm{A}}_{\overrightarrow F }}{\rm{ = }}\left| {{{\rm{A}}_{\overrightarrow P }}} \right| = \Delta {{\rm{W}}_t} = {{\rm{W}}_t} - {{\rm{W}}_{t0}} = 96000 - 0 = 96000J\)
Câu 62 :
Trong công viên giải trí, một xe có khối lượng m = 100kg chạy trên đường ray có mặt cắt như hình vẽ. Độ cao của các điểm A, B, C, D, E được tính đối với mặt đất và có các giá trị: \({z_A}\; = 20m;{z_B}\; = 10m;{z_C}\; = 15m;{z_D}\; = 5m;{z_E}\; = 18m\). Lấy g = 10m/s2. Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến B; từ B đến C; từ A đến D; từ A đến E có giá trị lần lượt là:
Đáp án : C Phương pháp giải :
Độ biến thiên thế năng: \(\Delta {{\rm{W}}_t} = {{\rm{W}}_{t1}} - {{\rm{W}}_{t2}}\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}m = 100kg\\{z_A}\; = 20m;{z_B}\; = 10m;{z_C}\; = 15m;{z_D}\; = 5m;{z_E}\; = 18m\\g = 10m/{s^2}\end{array} \right.\) Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến B: \(\begin{array}{l}\Delta {{\rm{W}}_{tAB}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tB}} = mg{z_A} - mg{z_B} = mg\left( {{z_A} - {z_B}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAB}} = 100.10.\left( {20 - 10} \right) = 10000J\end{array}\) Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ B đến C: \(\begin{array}{l}\Delta {{\rm{W}}_{tBC}} = {{\rm{W}}_{tB}} - {{\rm{W}}_{tC}} = mg{z_B} - mg{z_C} = mg\left( {{z_B} - {z_C}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tBC}} = 100.10.\left( {10 - 15} \right) = - 5000J\end{array}\) Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến D: \(\begin{array}{l}\Delta {{\rm{W}}_{tAD}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tD}} = mg{z_A} - mg{z_D} = mg\left( {{z_A} - {z_D}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAD}} = 100.10.\left( {20 - 5} \right) = 15000J\end{array}\) Độ biến thiên thế năng của xe trong trọng trường khi nó di chuyển từ A đến E: \(\begin{array}{l}\Delta {{\rm{W}}_{tAE}} = {{\rm{W}}_{tA}} - {{\rm{W}}_{tE}} = mg{z_A} - mg{z_E} = mg\left( {{z_A} - {z_E}} \right)\\ \Rightarrow \Delta {{\rm{W}}_{tAE}} = 100.10.\left( {20 - 18} \right) = 2000J\end{array}\)
Câu 63 :
Một lò xo có độ cứng \(k = 40N/m\), chọn mốc thế năng ở vị trí lò xo không biến dạng thì khi lò xo dãn \(3cm\) thế năng đàn hồi của lò xo bằng
Đáp án : A Phương pháp giải :
Thế năng đàn hồi là dạng năng lượng của một vật chịu tác dụng của lực đàn hồi. Công thức tính thế năng đàn hồi của một lò xo ở trạng thái có biến dạng \(\Delta l\) là: \({W_t} = \dfrac{1}{2}k.{\left( {\Delta l} \right)^2}\) Lời giải chi tiết :
Chọn mốc thế năng tại vị trí lò xo không biến dạng. Độ biến dạng của lò xo: \(\Delta l = 3cm = 0,03m\) Thế năng đàn hồi của lò xo bằng: \({W_t} = \dfrac{1}{2}k.{\left( {\Delta l} \right)^2} = \dfrac{1}{2}.40.0,{03^2} = 0,018J\)
|




















Danh sách bình luận