Trắc nghiệm Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán 7 Kết nối tri thứcĐề bài
Câu 1 :
Cho tam giác ABC và tam giác KHI có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Câu 2 :
Cho tam giác DEF và tam giác HKG có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), DE = HK.Biết \(\widehat F = {80^0}\). Số đo góc G là:
Câu 3 :
Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Kẻ MH vuông góc với AB (H thuộc AB) và MK vuông góc với AC (K thuộc AC). Khẳng định nào sau đây không đúng:
Câu 4 :
Cho góc nhọn xBy. Kẻ tia phân giác Bm của góc xBy. Trên tia Bm lấy điểm M bất kì. Kẻ MH vuông góc với Bx, MK vuông góc với By (H \( \in \) Bx, K \( \in \) By). Khẳng định sai là:
Câu 5 :
Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\) Chọn câu đúng.
Câu 6 :
Cho tam giác ABC có \(\widehat B = 40^\circ ;\widehat C = 70^\circ \). Kẻ BD vuông góc với AC. Biết AD = 4 cm, tính độ dài cạnh AC.
Câu 7 :
Cho tam giác\(ABC\)và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\)và tam giác \(NPM\)bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Câu 8 :
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khẳng định đúng là:
Câu 9 :
Cho tam giác ABC. Từ A vẽ một cung tròn có bán kính bằng BC và từ C vẽ một cung tròn có bán kính bằng AB, hai cung tròn này cắt nhau tại D (D nằm khác phía của B đối với AC). Kẻ AH vuông góc với BC (H thuộc BC) và CK vuông góc với AD (K thuộc AD). Chọn câu sai
Câu 10 :
Cho tam giác ABC có AB < AC. Cho M là trung điểm của cạnh BC. Tia phân giác của góc A cắt đường thẳng qua M, vuông góc với BC tại điểm I. Qua I kẻ IH vuông góc với AB, IK vuông góc với AC ( H \( \in \) đường thẳng AB, K \( \in \) đường thẳng AC). Phát biểu nào sau đây sai:
Câu 11 :
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Câu 12 :
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat M = {90^0},\,\widehat C = \widehat P\). Cần thêm một điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
Câu 13 :
Cho tam gác $ABC$ và tam giác $DEF$ có \(\widehat B = \widehat E = {90^0},\,AC = DF,\,\,\widehat A = \widehat F\). Phát biểu nào trong các phát biểu sau đây là đúng
Câu 14 :
Cho tam giác \(ABC\) và tam giác $KHI$ có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Câu 15 :
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE$ , \(\widehat B = \widehat E\) , \(\widehat A = \widehat D = 90^\circ \). Biết $AC = 9cm.$ Độ dài $DF$ là:
Câu 16 :
Cho tam giác $DEF$ và tam giác $HKI$ có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc \(I\) là:
Câu 17 :
Cho hình vẽ sau. Chọn câu đúng. 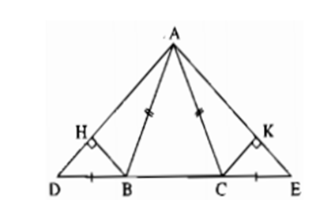
Câu 18 :
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM\) là tia phân giác của góc \(A\). Khi đó, tam giác \(ABC\) là tam giác gì?
Câu 19 :
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng
Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\) Câu 20
Chọn câu đúng.
Câu 21
Tính số đo góc \(DBK.\)
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\). Câu 22
Tam giác \(AMN\) là tam giác gì?
Câu 23
So sánh \(BE\) và \(CF.\)
Câu 24
Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Cho tam giác ABC và tam giác KHI có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Đáp án : A Phương pháp giải :
Sử dụng trường hợp bằng nhau cạnh huyền – cạnh góc vuông của tam giác vuông Lời giải chi tiết :
Xét tam giác ABC và tam giác KHI có: \(\begin{array}{l}\widehat A = \widehat K = 90^\circ \\AB = KH\;\;\left( {gt} \right)\\BC = HI\;\;\;\left( {gt} \right)\end{array}\) \( \Rightarrow \Delta ABC = \Delta KHI\) (cạnh huyền - cạnh góc vuông)
Câu 2 :
Cho tam giác DEF và tam giác HKG có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), DE = HK.Biết \(\widehat F = {80^0}\). Số đo góc G là:
Đáp án : B Phương pháp giải :
Sử dụng trường hợp bằng nhau cạnh góc vuông-góc nhọn của tam giác vuông để suy ra hai góc tương ứng bằng nhau, từ đó tính được số đo góc nhọn. Lời giải chi tiết :
Xét tam giác DEF và tam giác HKG có \(\begin{array}{l}\widehat D = \widehat H = {90^0}\\\widehat E = \widehat K\;\;\left( {gt} \right)\\DE = HK\;\;\left( {gt} \right)\end{array}\) \( \Rightarrow \Delta DEF = \Delta HKG\) (g.c.g). \( \Rightarrow \widehat F = \widehat G = 80^\circ \) ( hai góc tương ứng)
Câu 3 :
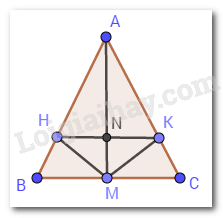
Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Kẻ MH vuông góc với AB (H thuộc AB) và MK vuông góc với AC (K thuộc AC). Khẳng định nào sau đây không đúng:
Đáp án : C Phương pháp giải :
Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau Lời giải chi tiết :
Xét \(\Delta AHM\) và \(\Delta AKM\) có: \(\widehat H = \widehat K = 90^\circ \;\;(gt)\) AM chung \(\widehat {HAM} = \widehat {KAM}\) (vì AM là tia phân giác góc A) Suy ra \(\Delta AHM = \Delta AKM\) (cạnh huyền – góc nhọn), Do đó \(MH = MK;\,AH = AK\) (các cặp cạnh tương ứng) nên khẳng định A, B đúng Xét \(\Delta BHM\) và \(\Delta CKM\) có: \(\begin{array}{l}\widehat H = \widehat K = 90^\circ \;(gt)\\HM = KM\;(cmt)\end{array}\) \(BM = MC\) (M là trung điểm của BC) Suy ra \(\Delta BHM = \Delta CKM\) (cạnh huyền - cạnh góc vuông) Do đó \( \widehat B = \widehat C\) ( hai góc tương ứng) nên khẳng định D đúng
Câu 4 :
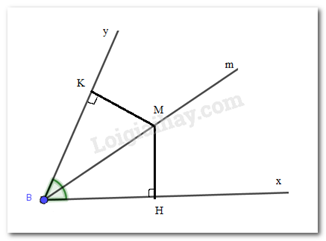
Cho góc nhọn xBy. Kẻ tia phân giác Bm của góc xBy. Trên tia Bm lấy điểm M bất kì. Kẻ MH vuông góc với Bx, MK vuông góc với By (H \( \in \) Bx, K \( \in \) By). Khẳng định sai là:
Đáp án : D Phương pháp giải :
Sử dụng các trường hợp bằng nhau của tam giác vuông, suy ra các cặp cạnh, cặp góc tương ứng bằng nhau. Lời giải chi tiết :
Vì Bm là tia phân giác của góc xBy nên \(\widehat {HBM} = \widehat {KBM}\) Xét tam giác vuông HBM và KBM, có: BM chung \(\widehat {HBM} = \widehat {KBM}\) Do đó \(\Delta HBM = \Delta KBM\) (cạnh huyền – góc nhọn) Suy ra HB = KB; MH = MK (2 cạnh tương ứng) nên khẳng định A,B đúng \(\widehat {BMH} = \widehat {BMK}\) (2 góc tương ứng), mà tia MB nằm giữa MH và MK nên MA là tia phân giác của góc HMK nên khẳng định C đúng
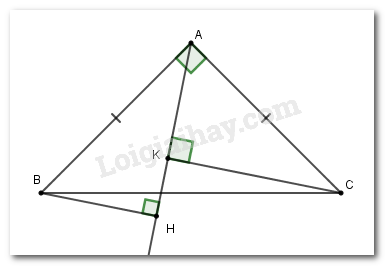
Câu 5 :
Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\) Chọn câu đúng.
Đáp án : D Phương pháp giải :
Chứng minh hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau Lời giải chi tiết :
Xét tam giác vuông \(BAD\) và \(BHD\) có \(AD\) chung \(\widehat {ABD} = \widehat {HBD}\) (tính chất tia phân giác) Nên \(\Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Câu 6 :
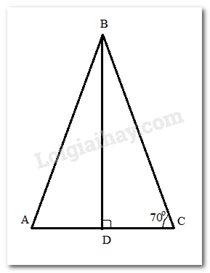
Cho tam giác ABC có \(\widehat B = 40^\circ ;\widehat C = 70^\circ \). Kẻ BD vuông góc với AC. Biết AD = 4 cm, tính độ dài cạnh AC.
Đáp án : B Phương pháp giải :
Áp dụng định lí tổng ba góc trong tam giác, suy ra các góc bằng nhau. Áp dụng trường hợp bằng nhau của tam giác vuông, suy ra các cạnh tương ứng bằng nhau Lời giải chi tiết :
Xét tam giác ABC, có \(\widehat A + \widehat {ABC} + \widehat C = 180^\circ \) ( tổng 3 góc trong tam giác bằng 180 độ) \(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 70^\circ = 180^\circ \\ \Rightarrow \widehat A = 70^\circ \\ \Rightarrow \widehat A = \widehat C\end{array}\) Trong \(\Delta \)ABD vuông tại D, có \(\widehat A + \widehat {ABD} = 90^\circ \) Trong \(\Delta \)CBD vuông tại D, có: \(\widehat C + \widehat {CBD} = 90^\circ \) \( \Rightarrow \widehat {ABD} = \widehat {CBD}\) Xét \(\Delta \)ABD và \(\Delta \)CBD , ta có: \(\widehat {ADB} = \widehat {CDB}( = 90^\circ )\) BD chung \(\widehat {ABD} = \widehat {CBD}\) \( \Rightarrow \)\(\Delta \)ABD = \(\Delta \)CBD ( g.c.g) \( \Rightarrow \) AD = CD ( 2 cạnh tương ứng) Mà AD = 4cm \( \Rightarrow \)CD = 4 cm Ta có: AC = AD + CD = 4 + 4 = 8 ( cm)
Câu 7 :
Cho tam giác\(ABC\)và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\)và tam giác \(NPM\)bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Đáp án : C Phương pháp giải :
Áp dụng trường hợp bằng nhau của tam giác vuông: cạnh huyền-cạnh góc vuông Lời giải chi tiết :
Ta có tam giác\(ABC\)và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \) mà BC, PM là hai cạnh góc vuông của hai tam giác \(ABC\) và \(NPM\) nên để hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là \(CA = MN.\)
Câu 8 :
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khẳng định đúng là:
Đáp án : D Phương pháp giải :
Chứng minh hai tam giác bằng nhau \(\Delta ABH = \Delta CAK\) suy ra các cạnh tương ứng bằng nhau Lời giải chi tiết :
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất) Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \) Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) ) \( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) nên \(BH = AK.\)( 2 cạnh tương ứng)
Câu 9 :
Cho tam giác ABC. Từ A vẽ một cung tròn có bán kính bằng BC và từ C vẽ một cung tròn có bán kính bằng AB, hai cung tròn này cắt nhau tại D (D nằm khác phía của B đối với AC). Kẻ AH vuông góc với BC (H thuộc BC) và CK vuông góc với AD (K thuộc AD). Chọn câu sai
Đáp án : C Phương pháp giải :
+) Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau, +) Sử dụng hai góc bằng nhau ở vị trí so le trong ta chứng minh được hai đường thẳng song song Lời giải chi tiết :
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\begin{array}{l}AC\;\;chung\\AB = CD\;(cmt)\\BC = DA\;(cmt)\\ \Rightarrow \Delta ABC = \Delta CDA(c - c - c)\end{array}\) \( \Rightarrow \widehat {ACB} = \widehat {CAD}\) (hai góc tương ứng) Mà 2 góc này ở vị trí so le trong nên AD // BC. Ta có: \(\widehat {ACB} = \widehat {CAD}\;\;(cmt) \Rightarrow \widehat {ACH} = \widehat {CAK}\) Xét \(\Delta AHC\) và \(\Delta CKA\) có: \(\begin{array}{l}AC\;chung\\\widehat H = \widehat K = 90^\circ \;(gt)\\\widehat {ACH} = \widehat {CAK}\;\;\left( {cmt} \right)\end{array}\) \( \Rightarrow \Delta AHC = \Delta CKA\) (cạnh huyền - góc nhọn) \( \Rightarrow AH = CK\) ( hai cạnh tương ứng). Do đó, A,B,D là các khẳng định đúng
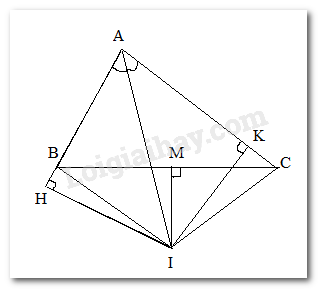
Câu 10 :
Cho tam giác ABC có AB < AC. Cho M là trung điểm của cạnh BC. Tia phân giác của góc A cắt đường thẳng qua M, vuông góc với BC tại điểm I. Qua I kẻ IH vuông góc với AB, IK vuông góc với AC ( H \( \in \) đường thẳng AB, K \( \in \) đường thẳng AC). Phát biểu nào sau đây sai:
Đáp án : C Phương pháp giải :
Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau Cộng, trừ đoạn thẳng suy ra các đẳng thức Lời giải chi tiết :
Xét tam giác vuông AIH và AIK có: AI chung \(\widehat {HAI} = \widehat {KAI}\) ( do AI là tia phân giác của góc BAC) \( \Rightarrow \Delta AIH = \Delta AIK\) ( cạnh huyền – góc nhọn) \( \Rightarrow \) AH = AK ; IH = IK ( các cạnh tương ứng) nên A đúng Xét tam giác vuông MBI và MCI có: MB = MC ( do M là trung điểm của BC) \(\widehat {BMI} = \widehat {CMI}( = 90^\circ )\) MI chung \( \Rightarrow \)\(\Delta MBI = \Delta MCI\) ( c.g.c) \( \Rightarrow \) BI = CI ( 2 cạnh tương ứng) Xét tam giác vuông HBI và KCI có: BI = CI ( cmt) HI = KI ( cmt) \( \Rightarrow \)\(\Delta HBI = \Delta KCI\) ( cạnh huyền – cạnh góc vuông) \( \Rightarrow \) HB = KC ( 2 cạnh tương ứng) nên D đúng Ta có: AB + AC = (AH – HB) + (AK + KC) = AK – KC + AK + KC = 2.AK ( vì AH = AK, HB = KC) \( \Rightarrow AK = \frac{{AB + AC}}{2}\) nên B đúng
Câu 11 :
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Đáp án : C Lời giải chi tiết :
Ta có tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \) mà \(BC;PM\) là hai cạnh góc vuông của hai tam giác \(ABC\) và \(NPM\) nên để hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là \(CA = MN.\)
Câu 12 :
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat M = {90^0},\,\widehat C = \widehat P\). Cần thêm một điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
Đáp án : A Lời giải chi tiết :
Ta có: \(\,\widehat C = \widehat P\), mà góc $C$ và góc $P$ là hai góc nhọn kề của hai tam giác $ABC$ và $MNP$ Do đó: để tam giác vuông $ABC$ và tam giác vuông $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn \(\widehat C\) và \(\widehat P\) của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện \(AC = MP.\)
Câu 13 :
Cho tam gác $ABC$ và tam giác $DEF$ có \(\widehat B = \widehat E = {90^0},\,AC = DF,\,\,\widehat A = \widehat F\). Phát biểu nào trong các phát biểu sau đây là đúng
Đáp án : A Lời giải chi tiết :
Xét tam giác $ABC$ và tam giác $FED$ có: + \(\widehat B = \widehat E = {90^0}\). + \(AC = DF\;\;\left( {gt} \right)\) + \(\,\,\widehat A = \widehat F\;\;\left( {gt} \right)\) \( \Rightarrow \Delta ABC = \Delta FED\) (cạnh huyền - góc nhọn)
Câu 14 :
Cho tam giác \(ABC\) và tam giác $KHI$ có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Đáp án : A Lời giải chi tiết :
Xét tam giác $ABC$ và tam giác $KHI$ có: \(\begin{array}{l}\widehat A = \widehat K = 90^\circ \\AB = KH\;\;\left( {gt} \right)\\BC = HI\;\;\;\left( {gt} \right)\end{array}\) \( \Rightarrow \Delta ABC = \Delta KHI\) (cạnh huyền - cạnh góc vuông)
Câu 15 :
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE$ , \(\widehat B = \widehat E\) , \(\widehat A = \widehat D = 90^\circ \). Biết $AC = 9cm.$ Độ dài $DF$ là:
Đáp án : C Phương pháp giải :
Sử dụng trường hợp bằng nhau cạnh góc vuông-góc nhọn của tam giác vuông để suy ra hai cạnh tương ứng bằng nhau, từ đó tính được độ dài cạnh Lời giải chi tiết :
Xét tam giác $ABC$ và tam giác $DEF$ có \(AB = DE\;\;\left( {gt} \right);\,\widehat B = \widehat E\;\;\left( {gt} \right);\,\widehat A = \widehat D = {90^0}.\) \( \Rightarrow \Delta ABC = \Delta DEF\)( cạnh góc vuông - góc nhọn) . \( \Rightarrow DF = AC = 9\,cm\) (hai cạnh tương ứng bằng nhau)
Câu 16 :
Cho tam giác $DEF$ và tam giác $HKI$ có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc \(I\) là:
Đáp án : B Phương pháp giải :
Sử dụng trường hợp bằng nhau cạnh góc vuông-góc nhọn của tam giác vuông để suy ra hai góc tương ứng bằng nhau, từ đó tính được số đo góc nhọn. Lời giải chi tiết :
Xét tam giác $DEF$ và tam giác $HKI$ có \(\widehat D = \widehat H = {90^0};\,\widehat E = \widehat K\;\;\left( {gt} \right);\,DE = HK\;\;\left( {gt} \right)\) \( \Rightarrow \Delta DEF = \Delta HKI\) (cạnh góc vuông - góc nhọn). \( \Rightarrow \widehat F = \widehat I = 80^\circ \) ( hai góc tương ứng)
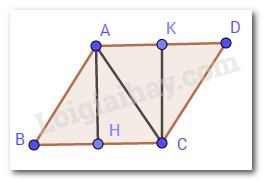
Câu 17 :
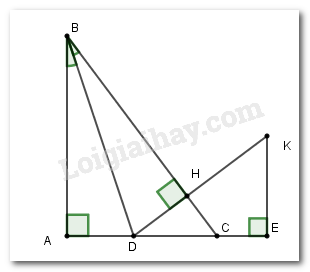
Cho hình vẽ sau. Chọn câu đúng. 
Đáp án : D Phương pháp giải :
+ Chứng minh hai tam giác \(BAD\) và \(CAE\) bằng nhau theo trường hợp cạnh- cạnh- cạnh để suy ra \(\widehat {DAB} = \widehat {CAE}\) + Từ đó chứng minh hai tam giác vuông \(AHB\) và \(AKC\) bằng nhau theo trường hợp cạnh huyền-góc nhọn. Lời giải chi tiết :
Vì tam giác \(ABC\) cân tại \(A\) (do \(AB = AC\) ) nên \(\widehat {ABC} = \widehat {ACB}\) (tính chất) (1) Lại có \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) và \(\widehat {ACB} + \widehat {ACE} = 180^\circ \) (hai góc kề bù) Suy ra \(\widehat {ABD} = 180^\circ - \widehat {ABC}\) ; \(\widehat {ACE} = 180^\circ - \widehat {ACB}\) (2) Từ (1) và (2) suy ra \(\widehat {ABD} = \widehat {ACE}\) Xét tam giác \(ABD\) và tam giác \(ACE\) có \(AB = AC;\,\)\(\widehat {ABD} = \widehat {ACE}\,\left( {cmt} \right);\)\(BD = CE\,\) Suy ra \(\Delta ABD = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {DAB} = \widehat {CAE}\) (hai góc tương ứng) Xét tam giác \(AHB\) và \(AKC\) có + \(\widehat H = \widehat K = 90^\circ \) + \(AB = AC\) + \(\widehat {DAB} = \widehat {CAE}\,\left( {cmt} \right)\) Suy ra \(\Delta AHB = \Delta AKC\,\left( {ch - gn} \right)\)
Câu 18 :
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM\) là tia phân giác của góc \(A\). Khi đó, tam giác \(ABC\) là tam giác gì?
Đáp án : D Phương pháp giải :
Ta sử dụng tính chất: Nếu một tam giác có đường trung tuyến trùng với đường phân giác thì tam giác đó là tam giác cân. Lời giải chi tiết :
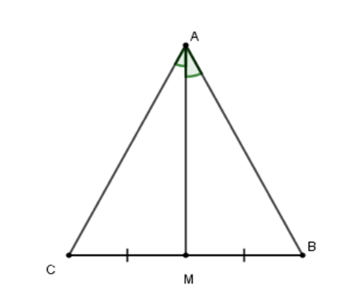 Tam giác \(ABC\) có \(AM\) vừa là đường trung tuyến vừa là đường phân giác nên \(\Delta BAC\) cân tại $A.$
Câu 19 :
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng
Đáp án : C Phương pháp giải :
+ Chứng minh hai tam giác bằng nhau \(\Delta ABH = \Delta CAK\) suy ra các cạnh tương ứng bằng nhau + Sử dụng định lý Py-ta-go Lời giải chi tiết :
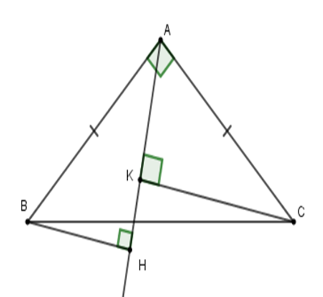
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất) Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \) Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) ) \( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) suy ra \(BH = AK.\) Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\) Xét tam giác \(ACK\), theo định lý Pytago: \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\) Từ (1) và (2) suy ra \(B{H^2} + C{K^2} = A{C^2}.\) Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\) Câu 20
Chọn câu đúng.
Đáp án : D Phương pháp giải :
Chứng minh hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau Lời giải chi tiết :
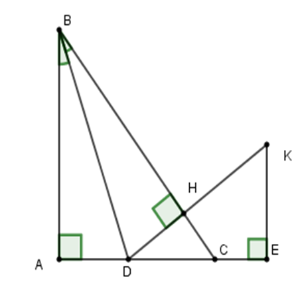 Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung \( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng). Câu 21
Tính số đo góc \(DBK.\)
Đáp án : A Phương pháp giải :
+ Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\) + Suy ra \(\widehat {ABF} = 90^\circ \) và \(AB = BF\) +Chứng minh \(\widehat {KBH} = \widehat {FBK}\) (dựa vào hai tam giác bằng nhau) + Lập luận để suy ra số đo góc \(DBK.\) Lời giải chi tiết :
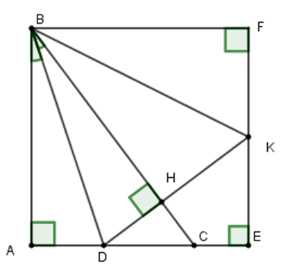 + Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\) Khi đó ta có \(ABFE\) là hình vuông nên \(\widehat {ABF} = 90^\circ \) và \(AB = BF\) Lại có \(AB = BH\) (ý trước) nên \(BH = BF\) Xét hai tam giác vuông \(BHK\) và \(BFK\) có \(BH = BF\left( {cmt} \right);\,BK\) cạnh chung Nên \(\Delta BHK = \Delta BFK\left( {ch - cgv} \right)\)\( \Rightarrow \widehat {FBK} = \widehat {HBK}\) Lại có \(\widehat {ABD} = \widehat {DBH}\) (do \(BD\) là phân giác góc \(\widehat {ABC}\) ) Nên \(\widehat {DBH} + \widehat {HBK} = \widehat {ABD} + \widehat {KBF} = \dfrac{{\widehat {DBH} + \widehat {HBK} + \widehat {ABD} + \widehat {KBF}}}{2}\)\(\dfrac{{\widehat {ABF}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \) Mà Vậy \(\widehat {DBK} = \widehat {DBH} + \widehat {HBK} = 45^\circ .\) Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\). Câu 22
Tam giác \(AMN\) là tam giác gì?
Đáp án : B Phương pháp giải :
- Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh \(\Delta ABM = \Delta ACN\), từ đó suy ra hai cạnh tương ứng bằng nhau để suy ra điều phải chứng minh. Lời giải chi tiết :
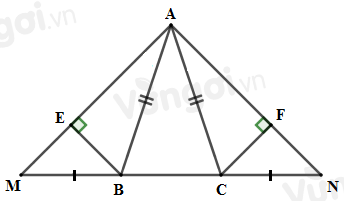 \(\Delta ABC\) cân tại \(A\) nên \(AB = AC,\,\widehat {ABC} = \widehat {ACB}\) (1) Mặt khác: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù) (2) \(\widehat {ACN} + \widehat {ACB} = {180^o}\) (kề bù) (3) Từ (1), (2) và (3) suy ra \(\widehat {ABM} = \widehat {ACN}\). Xét \(\Delta ABM\) và \(\Delta ACN\) có: \(AB = AC\,\,(cmt)\) \(\widehat {ABM} = \widehat {ACN}\,\,(cmt)\) \(BM = CN\,\,(gt)\) \( \Rightarrow \Delta ABM = \Delta ACN\,\,(c.g.c)\) \( \Rightarrow AM = AN\) (hai cạnh tương ứng). \( \Rightarrow \Delta AMN\) cân tại \(A.\) Câu 23
So sánh \(BE\) và \(CF.\)
Đáp án : C Phương pháp giải :
- Chứng minh \(\Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn) từ đó suy ra hai cạnh tương ứng bằng nhau. Lời giải chi tiết :
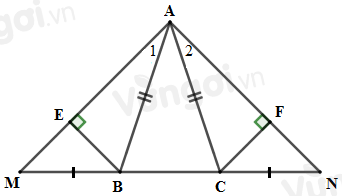 Sử dụng kết quả câu trước ta có \(\Delta ABM = \Delta ACN\,\,\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng). Xét hai tam giác vuông \(ABE\) và \(ACF\) có: \(\widehat {AEB} = \widehat {AFC} = {90^o}\) \(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\)) \(\widehat {{A_1}} = \widehat {{A_2}}\,\,(cmt)\) \( \Rightarrow \Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn) \( \Rightarrow BE = CF\) (hai cạnh tương ứng). Câu 24
Chọn câu đúng.
Đáp án : A Phương pháp giải :
- Sử dụng kết quả câu trước \(\Delta ABE = \Delta ACF\) nên \(BE = CF\) (hai cạnh tương ứng). Từ đó chứng minh \(\Delta BME = \Delta CNF\) (cạnh huyền – cạnh góc vuông). Lời giải chi tiết :
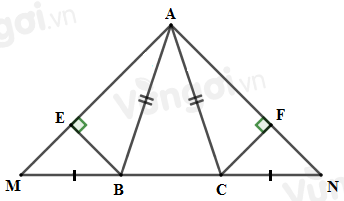 Sử dụng kết quả câu trước \(\Delta ABE = \Delta ACF\) nên \(BE = CF\) (hai cạnh tương ứng). Xét hai tam giác vuông \(BME\) và \(CNF\) có: \(\widehat {BEM} = \widehat {CFN} = {90^o}\) \(BE = CF\,\,(cmt)\) \(MB = NC\,\,(gt)\) \( \Rightarrow \Delta BME = \Delta CNF\) (cạnh huyền – cạnh góc vuông).
|



















Danh sách bình luận