Trắc nghiệm Bài 11: Định lí và chứng minh định lí Toán 7 Kết nối tri thứcĐề bài
Câu 1 :
Chứng minh định lý là
Câu 2 :
Trong các câu sau, câu nào không cho một định lí:
Câu 3 :
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
Câu 4 :
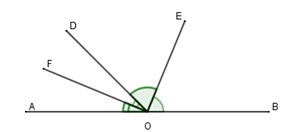
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
Câu 5 :
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
Câu 8 :
Chọn câu đúng.
Câu 9 :
Chọn khẳng định đúng:
Câu 10 :
Chọn câu sai:
Câu 11 :
Trong các câu sau, câu nào cho một định lí
Lời giải và đáp án
Câu 1 :
Chứng minh định lý là
Đáp án : A Phương pháp giải :
Sử dụng định nghĩa “chứng minh định lý”. Lời giải chi tiết :
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Câu 2 :
Trong các câu sau, câu nào không cho một định lí:
Đáp án : D Phương pháp giải :
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết :
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” + “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.” + “Hai góc đối đỉnh thì bằng nhau” Câu D không là định lí vì khẳng định D sai
Câu 3 :
Cho định lý: “Nếu hai đường thẳng song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
Đáp án : B Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Câu 4 :
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
Đáp án : A Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\). Kết luận: \(OE \bot OF\)
Câu 5 :
Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
Đáp án : B Phương pháp giải :
Xét vị trí của góc A1 so với góc B1 rồi xét giả thiết của từng định lý Lời giải chi tiết :
Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b Vậy định lý là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”
Đáp án : C Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Đáp án : A Phương pháp giải :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết :
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Câu 8 :
Chọn câu đúng.
Đáp án : D Phương pháp giải :
Lý thuyết về định lí Lời giải chi tiết :
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Câu 9 :
Chọn khẳng định đúng:
Đáp án : D Phương pháp giải :
Xét tính đúng, sai của từng khẳng định Lời giải chi tiết :
+ Tia phân giác của 2 góc đối đỉnh là đối nhau nên A sai + 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau nên B sai + 2 góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau chưa chắc đã đối đỉnh nên C sai + 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau nên là 2 cạnh của 1 góc bẹt. Do đó D đúng.
Câu 10 :
Chọn câu sai:
Đáp án : A Phương pháp giải :
Lý thuyết về định lí Lời giải chi tiết :
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …” Các khẳng định B,C,D đúng .
Câu 11 :
Trong các câu sau, câu nào cho một định lí
Đáp án : A Phương pháp giải :
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết :
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” Chú ý
Câu D sai vì ta cần hai đường thẳng phân biệt.
|














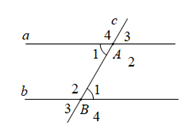
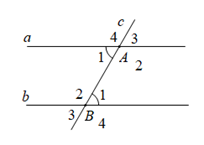





Danh sách bình luận