Trắc nghiệm Bài 33: Quan hệ giữa ba cạnh trong một tam giác Toán 7 Kết nối tri thứcĐề bài
Câu 1 :
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Câu 2 :
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Câu 3 :
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
Câu 4 :
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Câu 5 :
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Câu 6 :
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
Câu 7 :
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
Câu 8 :
Cho hình vẽ dưới đây. Chọn câu đúng.
Câu 9 :
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
Lời giải và đáp án
Câu 1 :
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Đáp án : D Phương pháp giải :
Áp dụng bất đẳng thức tam giác. Lời giải chi tiết :
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.
Câu 2 :
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Đáp án : C Phương pháp giải :
Ta kiểm tra tổng độ dài 2 đoạn thẳng ngắn hơn có lớn hơn độ dài đoạn thẳng dài nhất hay không. Nếu thỏa mãn thì 3 đoạn thẳng đã cho ghép được thành 1 tam giác. Lời giải chi tiết :
+ Xét bộ ba: $3cm,5cm,7cm.$ Ta có: \(3 + 5 = 8 > 7\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,7cm$ lập thành một tam giác. Loại đáp án A. + Xét bộ ba: $4cm,5cm,6cm$. Ta có: \(4 + 5 = 9 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $4cm,5cm,6cm$ lập thành một tam giác. Loại đáp án B. + Xét bộ ba: $2cm,5cm,7cm.$ Ta có: \(2 + 5 = 7\) (không thỏa mãn bất đẳng thức tam giác) nên bộ ba $2cm,5cm,7cm$ không lập thành một tam giác. Chọn đáp án C. + Xét bộ ba: $3cm,5cm,6cm.$ Ta có: \(3 + 5 = 8 > 6\) (thỏa mãn bất đẳng thức tam giác) nên bộ ba $3cm,5cm,6cm$ lập thành một tam giác. Loại đáp án D.
Câu 3 :
Cho \(\Delta ABC\) có cạnh $AB = 2cm$ và cạnh \(BC = 6cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số tự nhiên chẵn.
Đáp án : D Phương pháp giải :
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác) Kết hợp điều kiện độ dài cạnh CA là số nguyên chẵn Lời giải chi tiết :
Theo bất đẳng thức tam giác ta có: \(6 - 2 < AC< 6 + 2 \Leftrightarrow 4 < AC < 8\). Vì độ dài $AC$ là số tự nhiên chẵn nên $AC = 6cm.$ Vậy độ dài cạnh $AC = 6cm.$
Câu 4 :
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 6\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Đáp án : C Phương pháp giải :
Áp dụng bất đẳng thức trong tam giác để tính cạnh \(AC.\) Từ đó tính chu vi tam giác \(ABC.\) Lời giải chi tiết :
Gọi độ dài cạnh $AC$ là \(x\left( {x > 0} \right)\). Theo bất đẳng thức tam giác ta có: \(6 - 1 < x < 6 + 1 \Leftrightarrow 5 < x < 7\). Vì $x$ là số nguyên nên $x = 6.$ Độ dài cạnh $AC = 6cm.$ Chu vi tam giác \(ABC\) là \(AB + BC + AC = 1 + 6 + 6 = 13\,cm.\)
Câu 5 :
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Đáp án : A Phương pháp giải :
- Áp dụng tính chất tam giác cân. - Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại. Lời giải chi tiết :
Giả sử \(\Delta ABC\) cân tại $A.$ - Trường hợp 1: \(AB = AC = 5cm \Rightarrow BC = 17 - 5 - 5 = 7cm.\) Ta có: \(AB + AC = 5 + 5 = 10 > BC = 7cm\) (thỏa mãn bất đẳng thức tam giác) - Trường hợp 2: \(BC = 5cm \Rightarrow AB = AC = \left( {17 - 5} \right):2 = 6cm\) Ta có: \(AB + BC = 5 + 6 = 11 > AC = 6cm\) (thỏa mãn bất đẳng thức tam giác) Vậy nếu \(\Delta ABC\) cân tại A có \(\left[ \begin{array}{l}AB = AC = 5cm \Rightarrow BC = 7cm\\BC = 5cm \Rightarrow AB = AC = 6cm\end{array} \right.\) Vậy \(BC = 7\,cm\) hoặc \(BC = 5\,cm.\)
Câu 6 :
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
Đáp án : B Phương pháp giải :
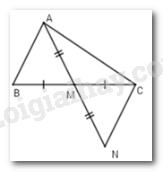
- Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$ - Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại. Lời giải chi tiết :
Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$ Vì $M$ là trung điểm của $BC$ (gt) \( \Rightarrow MB = MC\) (tính chất trung điểm) Xét \(\Delta MAB\) và \(\Delta MNC\) có: \(MB = MC\left( {cmt} \right)\) \(\widehat {AMB} = \widehat {NMC}\) (đối đỉnh) \(AM = MN\left( {gt} \right)\) \( \Rightarrow \Delta MAB = \Delta MNC\left( {c - g - c} \right)\) \( \Rightarrow NC = AB\left( 1 \right)\) (2 cạnh tương ứng) Xét \(\Delta ACN\) có: \(AN < AC + CN\left( 2 \right)\) (bất đẳng thức tam giác) Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow AN < AC + AB\). Mặt khác, \(AN = 2AM\left( {gt} \right) \Rightarrow 2AM < AB + AC.\)
Câu 7 :
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
Đáp án : A Phương pháp giải :
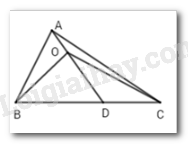
- Gọi giao điểm của $AO$ và $BC$ là $D.$ - Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại. Lời giải chi tiết :
Gọi giao điểm của $AO$ và $BC$ là $D.$ Do $O$ nằm trong \(\Delta ABC\) nên $D$ nằm giữa $B$ và $C$\( \Rightarrow BC = BD + DC\left( * \right)\) Xét \(\Delta ABD\) có: \(AD < AB + BD\) (bất đẳng thức tam giác) \( \Rightarrow OA + OD < AB + BD\left( 1 \right)\) Xét \(\Delta OCD\) có: \(OC < OD + DC\left( 2 \right)\) (bất đẳng thức tam giác) Cộng vế với vế của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được: \(OA + OD + OC < AB + BD + OD + DC\) \( \Rightarrow OA + OC < AB + BD + DC\left( {**} \right)\) Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta có: \(OA + OC < AB + BC.\)
Câu 8 :
Cho hình vẽ dưới đây. Chọn câu đúng.
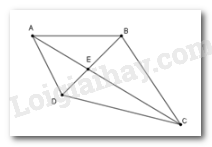
Đáp án : B Phương pháp giải :
Sử dụng quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia. Lời giải chi tiết :
Áp dụng quan hệ giữa ba cạnh của một tam giác: Xét tam giác \(AED\) có \(AE + ED > AD\,\,\,\left( 1 \right)\) Xét tam giác \(ECD\) có \(CE + DE > CD\,\,\left( 2 \right)\) Xét tam giác \(EBC\) có \(EB + EC > BC\,\left( 3 \right)\) Xét tam giác \(ABE\) có \(AE + EB > AB\,\,\,\left( 4 \right)\) Từ \(\left( 1 \right);\left( 2 \right);\left( 3 \right);\left( 4 \right)\) ta có \(AE + DE + CE + DE + BE + CE + AE + BE > AD + CD + BC + AB\) Mà \(AE + EC = AC;\,DE + BE = BD\) nên \(2\left( {AC + BD} \right) > AB + BC + CD + DA\) .
Câu 9 :
Cho \(\Delta ABC\) có \(D\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
Đáp án : B Phương pháp giải :
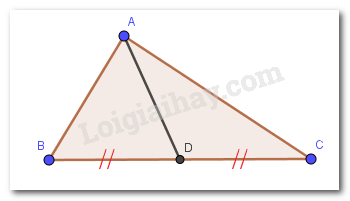
- Nối đoạn thẳng AD. - Áp dụng bất đẳng thức tam giác chứng minh: \(AD < AC + CD\), \(AD < AB + DB\). Từ đó lập luận suy ra điều phải chứng minh. Lời giải chi tiết :
Nối đoạn thẳng AD. Xét \(\Delta ADC\) có: \(AD < AC + CD\) (bất đẳng thức tam giác) (1) Xét \(\Delta ADB\) có: \(AD < AB + DB\) (bất đẳng thức tam giác) (2) Vì \(D\) là trung điểm của \(BC\) (gt) nên \(D\) nằm giữa \(B\) và \(C\) ta có: \(CD + DB = BC.\) Cộng vế với vế của (1) và (2), ta được: \(\begin{array}{l}AD + AD < AC + CD + AB + DB\\ \Rightarrow 2AD < AB + \left( {CD + DB} \right) + AC\\ \Rightarrow 2AD < AB + BC + AC\\ \Rightarrow AD < \dfrac{{AB + BC + AC}}{2}\end{array}\) Do đó \(AD\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
|
