Lý thuyết Tập hợp các số thực SGK Toán 7 - Kết nối tri thức

1. Khái niệm số thực và trục số thực

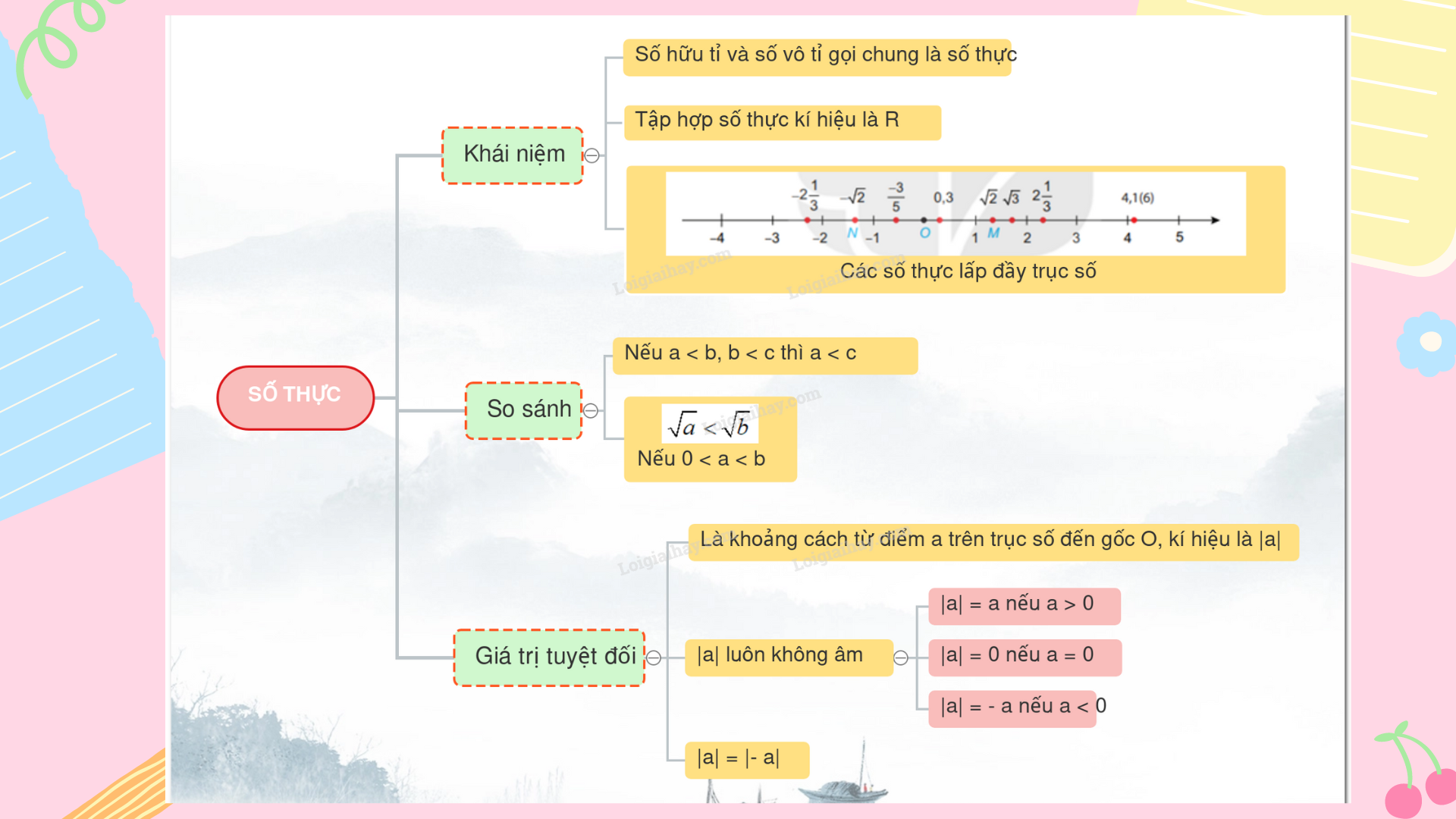
* Số hữu tỉ và số vô tỉ gọi chung là số thực

* Tập hợp các số thực được kí hiệu là R.

Chú ý: + Mỗi số thực a đều có một số đối là –a

+ Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.

* Trục số thực được biểu diễn bởi 1 số điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Chú ý: Các số thực lấp đầy trục số.

2. Thứ tự trong tập hợp các số thực

a) So sánh 2 số thực:

* Các số thực đều viết được dưới dạng số thập phân ( hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.

Ví dụ:

0,322 … < 0,324… nên 0,3(2) < 0,324…

* Với 2 số thực bất kì, ta luôn có hoặc a = b hoặc a > b hoặc a < b

* Nếu a < b ; b < c thì a < c ( Tính chất bắc cầu)

* Nếu a < b thì điểm a nằm trước điểm b trên trục số

Chú ý: Nếu 0 < a < b thì \(\sqrt a  < \sqrt b \)

Ví dụ: Vì 3 < 4 nên \(\sqrt 3  < \sqrt 4  = 2\)

3. Giá trị tuyệt đối của một số thực

Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là |a|

Nhận xét:

+ Hai số đối nhau thì có giá trị tuyệt đối bằng nhau

+ Giá trị tuyệt đối của 0 là 0

+ Giá trị tuyệt đối của một số dương là chính nó

+ Giá trị tuyệt đối của một số âm là số đối của nó

+ Giá trị tuyệt đối của một số thực luôn không âm.

Ví dụ: |2,3| = 2,3

|-2,3| = 2,3

|-2,3| = |2,3|