Lý thuyết Hàm số y = ax² (a ≠ 0) và đồ thị Toán 9 Cùng khám phá1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\). Quảng cáo
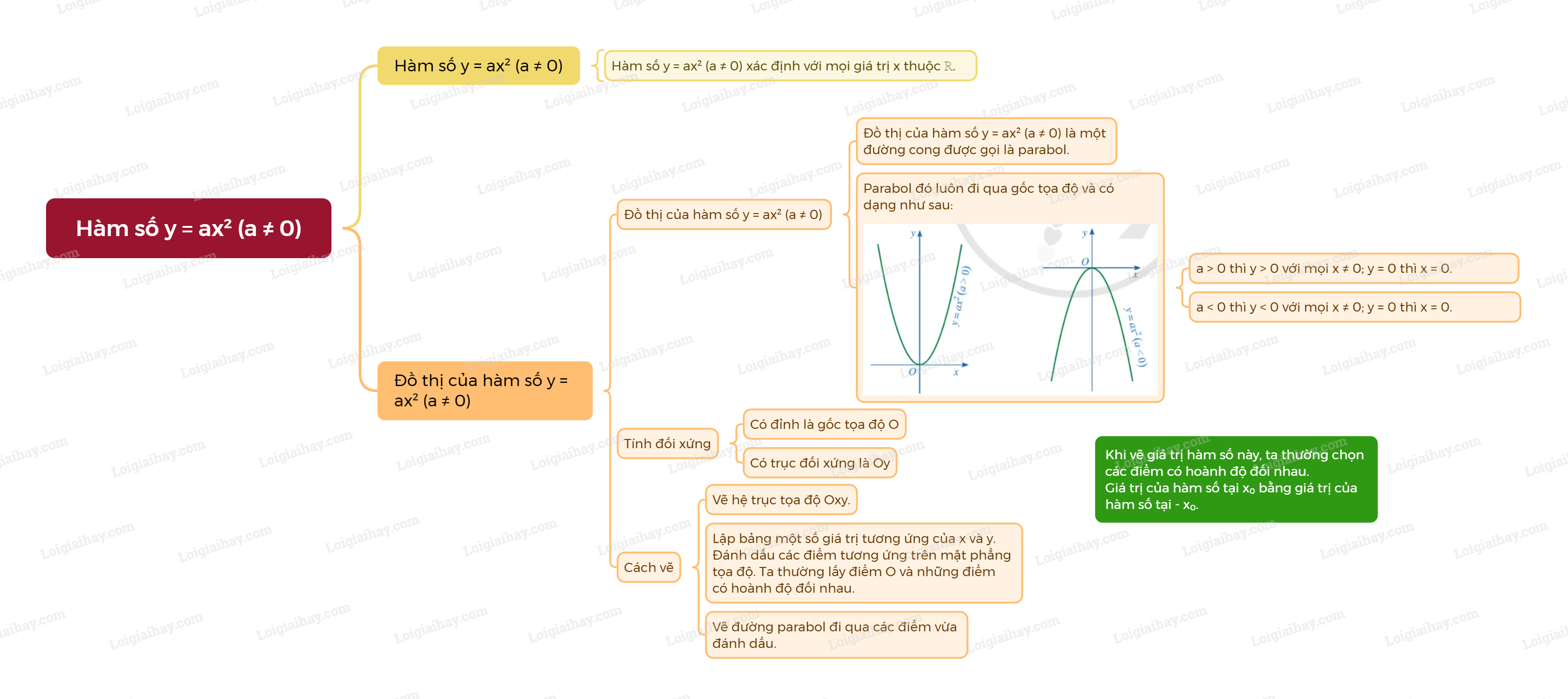
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\). 2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Lưu ý: - Cho hàm số \(y = a{x^2}\left( {a \ne 0} \right)\). + Nếu \(a > 0\) thì \(y > 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\). + Nếu \(a < 0\) thì \(y < 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\). - Vì đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ giá trị của hàm số này, ta thường chọn những điểm có hoành độ đối nhau. Chỉ cần tính giá trị của hàm số tại \({x_0}\), ta suy ra được giá trị của hàm số tại \( - {x_0}\) vì \(a{\left( { - x{ _0}} \right)^2} = a{x_0}^2\) Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
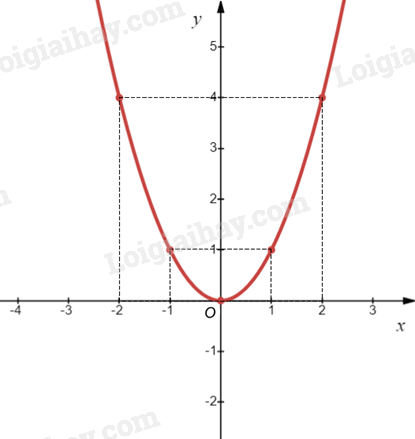
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\). Bảng giá trị của hàm số:
Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
|





















Danh sách bình luận