Giải mục 1 trang 2, 3 SGK Toán 9 tập 2 - Cùng khám pháViết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
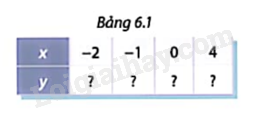
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 2 SGK Toán 9 Cùng khám phá Viết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm. Phương pháp giải: Dựa vào công thức diện tích tam giác vuông cân: S = \(\frac{1}{2}{x^2}\) (x là độ dài cạnh góc vuông). Thay lần lượt x = 2; x = 2,5; x = 6 để tính S. Lời giải chi tiết: Ta có hàm số biểu thị diện tích S = \(\frac{1}{2}{x^2}\) Với x = 2 ta có S = \(\frac{1}{2}{.2^2} = 2\)cm2 Với x = 2,5 ta có S = \(\frac{1}{2}.2,{5^2} = \frac{{25}}{8}\)cm2 Với x = 6 ta có S = \(\frac{1}{2}{.6^2} = 18\)cm2 LT1 Trả lời câu hỏi Luyện tập 1 trang 2 SGK Toán 9 Cùng khám phá Cho hàm số \(y = a{x^2}\). a) Tìm a khi biết x = 2 thì y = - 1. b) Tính các giá trị tương ứng của hàm số trong bảng 6.1
Phương pháp giải: Thay x = 2; y = -1 vào \(y = a{x^2}\) để tìm a. Thay lần lượt x = -2; x = -1; x = 0; x = 4 để tìm y. Lời giải chi tiết: a) Thay x = 2; y = -1 vào \(y = a{x^2}\) ta có: \(\begin{array}{l} - 1 = a{.2^2}\\a = - \frac{1}{4}\end{array}\) b) \(y = - \frac{1}{4}{x^2}\) Với x = -2 thì \(y = - \frac{1}{4}{\left( { - 2} \right)^2} = - \frac{1}{4}.4 = - 1\) Với x = -1 thì \(y = - \frac{1}{4}{\left( { - 1} \right)^2} = - \frac{1}{4}.1 = - \frac{1}{4}\) Với x = 0 thì \(y = - \frac{1}{4}{.0^2} = 0\) Với x = 4 thì \(y = - \frac{1}{4}{\left( 4 \right)^2} = - \frac{1}{4}.16 = - 4\)
VD1 Trả lời câu hỏi Vận dụng 1 trang 3 SGK Toán 9 Cùng khám phá Một vật rơi ở độ cao 80 m sao với mặt đất. Quãng đường chuyển động s (m) của vật rơi phụ thuộc vào thời gian t (s) bởi công thức s = 5t2. a) Tính quãng đường chuyển động của vật sau 2 giây. b) Hỏi sau bao lâu vật này tiếp đất? Phương pháp giải: Thay t = 2 vào s = 5t2 để tìm s. Thay s = 80 vào s = 5t2 để tìm t (t > 0). Lời giải chi tiết: a) Quãng đường chuyển động của vật sau 2 giây là: s = 5.22 = 20 (m) b) Để vật tiếp đất thì quãng đường vật đi được là 80 m thay vào s = 5t2 (t > 0) ta có: \(\begin{array}{l}5{t^2} = 80\\{t^2} = 16\\\left[ {\begin{array}{*{20}{c}}{t = 4(TM)}\\{t = - 4(L)}\end{array}} \right.\end{array}\) Vậy sau 4 giây thì vật tiếp đất.
|





















Danh sách bình luận