Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Kết nối tri thức1. Khái niệm bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn Quảng cáo
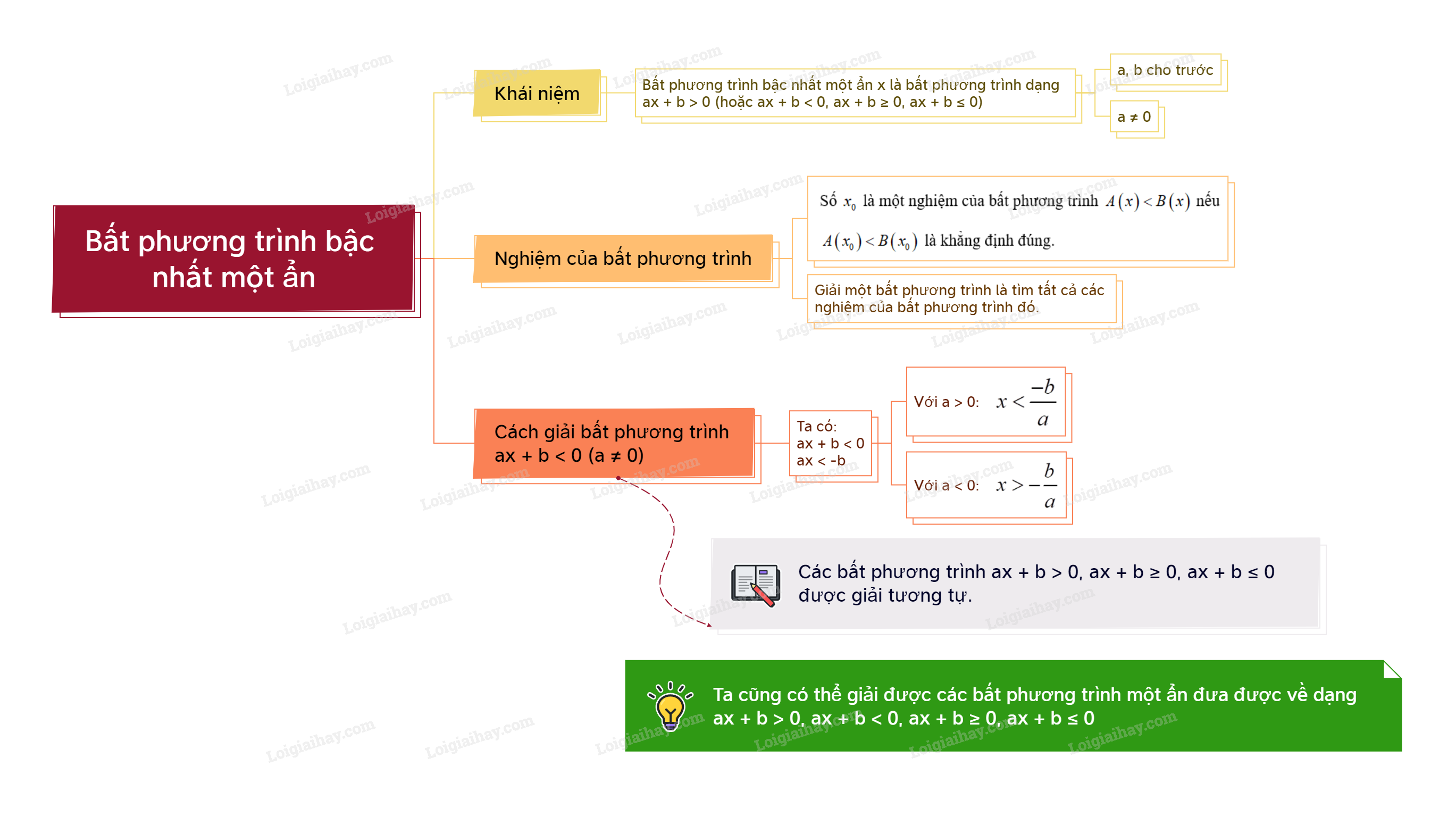
1. Khái niệm bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn
Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x. \({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai. \(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y. Nghiệm của bất phương trình
Ví dụ: Số -2 là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\). Số 6 không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\). 2. Cách giải bất phương trình bậc nhất một ẩn
Chú ý: Các bất phương trình \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\) được giải tương tự. Ví dụ: Giải bất phương trình \( - 2x - 4 > 0\) Lời giải: Ta có: \(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\) Vậy nghiệm của bất phương trình là \(x < - 2\). Chú ý: Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng \(ax + b < 0\), \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\).
|




















Danh sách bình luận