Giải mục II trang 69 SGK Toán 10 tập 2 - Cánh diềub) Tìm tọa độ của M theo tọa độ của A và B Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G ( minh họa ở Hình 20) Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB. Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
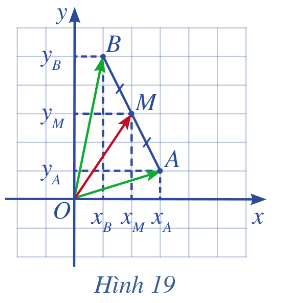
Hoạt động 2 Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\). Gọi \(M\left( {{x_M},{y_M}} \right)\) là trung điểm của đoạn thẳng AB (minh họa hình 19). a) Biểu diễn vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \). b) Tìm tọa độ của M theo tọa độ của A và B.
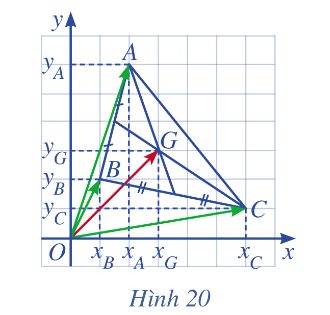
Lời giải chi tiết: a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\). b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có: \(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\). Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) \) \(= \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\). Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\). Hoạt động 3 Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G (minh họa ở Hình 20). a) Biểu diễn vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \). b) Tìm tọa độ G theo tọa độ của A, B, C.
Lời giải chi tiết: a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\). b) Do tọa độ ba điểm A, B và C là: \(A\left( {{x_A},{y_A}} \right)\), \(B\left( {{x_B},{y_B}} \right)\), \(C\left( {{x_C},{y_C}} \right)\) nên ta có: \(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right)\), \(\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\), \(\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\). Vậy \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) \) \(= \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\). Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\). Luyện tập – vận dụng 3 Cho hai điểm A(2; 4) và M(5; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB. Lời giải chi tiết: Giả sử B có tọa độ: \(B\left( {{x_B},{y_B}} \right)\). Do M là trung điểm của đoạn thẳng AB nên: \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A}\\{y_B} = 2{y_M} - {y_A}\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2.5 - 2 = 8\\{y_B} = 2.7 - 4 = 10\end{array} \right.\) Vậy tọa độ điểm B là: \(B\left( {8;10} \right)\). Luyện tập – vận dụng 4 Cho ba điểm A(-1; 1), B(1; 5), G(1; 2). a) Chứng minh ba điểm A, B, G không thẳng hàng. b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC. Lời giải chi tiết: a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right)\), \(\overrightarrow {AG} = \left( {2;1} \right)\). Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng. b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\). Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\) Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\).
|




















Danh sách bình luận