Giải mục 2 trang 32, 33 SGK Toán 7 tập 2 - Kết nối tri thứcCho hai đa thức P = x^4 + 3x^3 – 5x^2 + 7x và Q = -x^3 + 4x^2 – 2x +1 Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
2. Trừ hai đa thức một biến HĐ 1 Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1 Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn. Phương pháp giải: + Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc. +Bước 2: Nhóm các hạng tử cùng bậc + Bước 3: Thu gọn Lời giải chi tiết: Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1) = x4 + 3x3 – 5x2 + 7x + x3 - 4x2 + 2x – 1 = x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1 = x4 + 4x3 – 9x2 + 9x – 1 HĐ 2 Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1 Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột. Phương pháp giải: Bước 1: Đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau Bước 2: Trừ theo từng cột Lời giải chi tiết: LT 2 Cho hai đa thức: M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5 Hãy tính hiệu M - N ( trình bày theo 2 cách) Phương pháp giải: Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc. Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột. Lời giải chi tiết: Cách 1: M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5) = 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5 = 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5) = 0,5x4 + (– 6x3 ) - x2 + 2x + (-4) = 0,5x4 – 6x3 - x2 + 2x – 4 Cách 2: VD 2 Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho: A + B = 2x5 + 5x3 – 2 A – C = x3 Phương pháp giải: B = (A + B) – A C = A – (A – C) Thực hiện phép trừ đa thức: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc rồi nhóm các hạng tử cùng bậc Lời giải chi tiết: Ta có: B = (A + B) – A = 2x5 + 5x3 – 2 – (x4 – 3x2 – 2x + 1) = 2x5 + 5x3 – 2 – x4 + 3x2 + 2x - 1 = 2x5 – x4 + 5x3 + 3x2 + 2x + (-2 – 1) = 2x5 – x4 + 5x3 + 3x2 + 2x – 3 C = A – (A – C) = x4 – 3x2 – 2x + 1 – x3 = x4 – x3– 3x2 – 2x + 1 Vậy B = 2x5 – x4 + 5x3 + 3x2 + 2x – 3 C = x4 – x3– 3x2 – 2x + 1
|














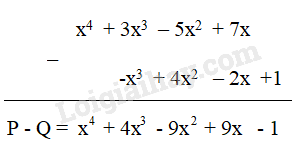
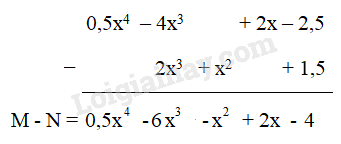






Danh sách bình luận