Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cùng khám pháVẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh: a) MA và MB; b) \(\widehat {AMO}\) và \(\widehat {BMO}\); c) \(\widehat {AOM}\) và \(\widehat {BOM}\). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
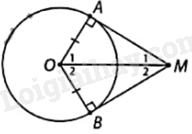
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 112 SGK Toán 9 Cùng khám phá Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh: a) MA và MB; b) \(\widehat {AMO}\) và \(\widehat {BMO}\); c) \(\widehat {AOM}\) và \(\widehat {BOM}\). Phương pháp giải: Đo hình và đưa ra kết luận. Lời giải chi tiết:
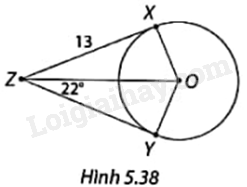
Tiến hành đo và so sánh ta có: a) \(MA = MB\) b) \(\widehat {AMO} = \widehat {BMO}\) c) \(\widehat {AOM} = \widehat {BOM}\) LT3 Trả lời câu hỏi Luyện tập 3 trang 113 SGK Toán 9 Cùng khám phá Trong Hình 5.38, ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y. Xác định số đo \(\widehat {XOY}\) và độ dài YZ.
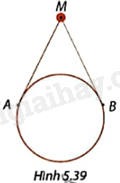
Phương pháp giải: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: + Điểm đó cách đều hai tiếp điểm; + Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm. Lời giải chi tiết: ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y nên + \(YZ = ZX = 13\) + OZ là tia phân giác góc XOY nên \(\widehat {XOY} = 2\widehat {ZOY}\) Vì ZY là tiếp tuyến của đường tròn tâm O nên \(ZY \bot OY\) nên tam giác ZOY vuông tại Y. Do đó, \(\widehat {ZOY} = {90^o} - \widehat {YZO} = {90^o} - {22^o} = {68^o}\) Vậy \(\widehat {XOY} = 2\widehat {ZOY} = {2.68^o} = {136^o}\). VD Trả lời câu hỏi Vận dụng trang 114 SGK Toán 9 Cùng khám phá Trong Hình 5.39, người ta dùng một đoạn dây gắn vào hai điểm A, B trên viền một chiếc gương tròn để treo gương vào điểm M. Biết tổng độ dài dây là 82cm, \(\widehat {AMB} = {52^o}\) và MA, MB tiếp xúc với viền gương. Tính đường kính của gương. Làm tròn kết quả đến đơn vị centimét.
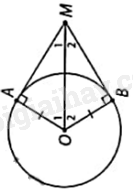
Phương pháp giải: + Vì MA, MB là tiếp tuyến của (O) nên \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB}\) và \(MA = MB\). + Tam giác AMO vuông tại A nên \(OA = AM.\tan AMO\), từ đó tính được OA. + Đường kính của gương là: \(2OA\). Lời giải chi tiết:
Gọi O là tâm của chiếc gương. Vì MA, MB là tiếp tuyến của (O) nên: + MO là tia phân giác góc AMB, suy ra: \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.52^o} = {26^o}\). + \(MA = MB = \frac{{82}}{2} = 41cm\). Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác AMO vuông tại A. Suy ra: \(OA = AM.\tan AMO = 41.\tan {26^o}\). Vậy đường kính của gương là: \(2OA = 2.41.\tan {26^o} \approx 40\left( {cm} \right)\)
|




















Danh sách bình luận