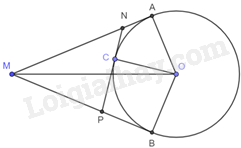
Giải bài tập 5.18 trang 114 SGK Toán 9 tập 1 - Cùng khám pháTừ điểm M nằm ngoài đường tròn (O; 5cm), \(MO = 13cm\), vẽ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). a) Tính độ dài MA và MB. b) Cho C là điểm bất kì thuộc đường tròn (O) và nằm trong góc AOB. Tiếp tuyến tại C của đường tròn cắt MA tại N và cắt MB tại P. Tính chu vi \(\Delta MNP\). Quảng cáo
Đề bài Từ điểm M nằm ngoài đường tròn (O; 5cm), \(MO = 13cm\), vẽ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). a) Tính độ dài MA và MB. b) Cho C là điểm bất kì thuộc đường tròn (O) và nằm trong góc AOB. Tiếp tuyến tại C của đường tròn cắt MA tại N và cắt MB tại P. Tính chu vi \(\Delta MNP\). Phương pháp giải - Xem chi tiết a) + Chứng minh tam giác MAO vuông tại A. Áp dụng định lí Pythagore vào tam giác MAO tính MA. + MA và MB là tiếp tuyến của đường tròn (O) nên \(MA = MB\). b) + Sử dụng tính chất của hai tiếp tuyến cắt nhau chứng minh \(NC = NA\), \(CP = BP\). + Chu vi tam giác MNP: \(MN + NP + MP\)\( = MN + NC + CP + MP\)\( = MN + NA + MP + PB\)\( = MA + MB\) Lời giải chi tiết
a) Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên tam giác MAO vuông tại A. Do đó, \(M{A^2} + A{O^2} = M{O^2}\) (định lí Pythagore) nên \(MA = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{13}^2} - {5^2}} = 12\left( {cm} \right)\). Vì MA và MB là tiếp tuyến của đường tròn (O) nên \(MA = MB = 12cm\). b) Vì NA và NC là tiếp tuyến của đường tròn (O) nên \(NC = NA\). Vì CP và PB là tiếp tuyến của đường tròn (O) nên \(CP = BP\). Chu vi tam giác MNP là: \(MN + NP + MP\)\( = MN + NC + CP + MP\)\( = MN + NA + MP + PB\)\( = MA + MB\)\( = 12 + 12\)\( = 24\left( {cm} \right)\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
