Giải bài tập 7 trang 78 SGK Toán 9 tập 2 - Cánh diều

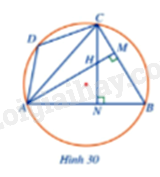
Đề bài

Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H (Hình 30). Chứng minh:

a) \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\)

b) \(\widehat {AHC} = \widehat {ADC.}\)

c) \(\widehat {ADC} = \widehat {BAM} + 90^\circ .\)

Lời giải chi tiết

a) Do tam giác ABC có hai đường cao AM, CN nên \(\widehat {HMB} = 90^\circ ,\widehat {BNH} = 90^\circ \)

Xét tứ giác HMBN có:

\(\begin{array}{l}\widehat {NHM} + \widehat {HMB} + \widehat {MBN} + \widehat {BNH} = 360^\circ \\\widehat {NHM} + \widehat {MBN} = 360^\circ  - \widehat {HMB} - \widehat {BNH}\\\widehat {NHM} + \widehat {MBN} = 360^\circ  - 90^\circ  - 90^\circ  = 180^\circ .\end{array}\)

Hay \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\)

b) Vì ABCD nội tiếp đường tròn nên  \(\widehat {CDA} + \widehat {ABC} = 180^\circ .\)

mà \(\widehat {MHN} + \widehat {ABC} = 180^\circ \) (câu a)

suy ra \(\widehat {CDA} = \widehat {MHN}\), hơn nữa \(\widehat {CHA} = \widehat {MHN}\) (đối đỉnh)

vậy \(\widehat {CHA} = \widehat {CDA.}\)

c) Xét tam giác AMB vuông tại M có: \(\widehat {BAM} + \widehat {AMB} = \widehat {BAM} + 90^\circ  = 180^\circ  - \widehat {MBA.}\)

Mà \(180^\circ  - \widehat {MBA} = \widehat {ADC}\) (do ABCD nội tiếp)

Vậy \(\widehat {ADC} = \widehat {BAM} + 90^\circ .\)