Giải bài tập 6 trang 78 SGK Toán 9 tập 2 - Cánh diềuCho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I. a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao? b) Chứng minh (Delta AIBbacksim Delta IDC) và IA.IC = IB.ID. Quảng cáo
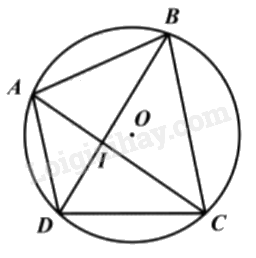
Đề bài Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I. a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao? b) Chứng minh \(\Delta AIB\backsim \Delta IDC\) và IA.IC = IB.ID. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Lý thuyết: Trong một đường tròn, hai góc nội tiếp cùng chắn 1 cung thì bằng nhau. b) Chỉ ra \(\Delta AIB\backsim \Delta IDC\) theo trường hợp g.g. Lời giải chi tiết
a) Do tứ giác ABCD nội tiếp đường tròn nên \(\widehat {ACD} = \widehat {ABD}\)(cùng chắn cung AD). b) Xét tam giác AIB và tam giác DIC có: \(\widehat {AIB} = \widehat {DIC}\) (đối đỉnh) \(\widehat {ACD} = \widehat {ABD}\)(cmt) Nên \(\Delta AIB\backsim \Delta DIC\)(g.g) Suy ra \(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) hay IA.IC = IB.ID (đpcm).
|




















Danh sách bình luận