Bài I.14 trang 17 SBT Vật Lí 12

Đề bài

Một con lắc đơn đang dao động điều hòa với biên độ góc \({\alpha _0}\) tại một nơi có gia tốc trọng trường là \(g\). Biết lực căng dây lớn nhất bằng \(1,02\) lần lực căng dây nhỏ nhất. Tính biên độ góc \({\alpha _0}\).

Lời giải chi tiết

Tại vị trí li độ góc \(\alpha \):

\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\\{{\rm{W}}_d} = mgl(\cos \alpha  - \cos {\alpha _0})\end{array} \right.\\ \Rightarrow v = \sqrt {2gl(\cos \alpha  - \cos {\alpha _0})} \end{array}\)

 

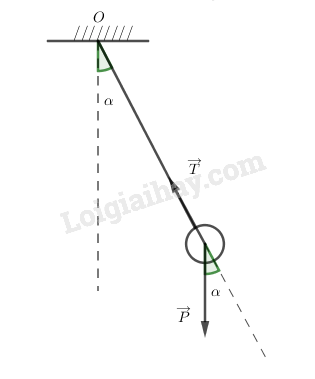
Áp dụng định luật II Niuton:

\(\overrightarrow T  + \overrightarrow P  = m\overrightarrow a \)

Chiếu theo phương hướng tâm:

\(\begin{array}{l}T - P\cos \alpha  = m{a_{ht}} = m\dfrac{{{v^2}}}{l}\\ \Leftrightarrow T = P\cos \alpha  + m\dfrac{{{v^2}}}{l}\\= mg\cos \alpha  + 2mg(\cos \alpha  - \cos {\alpha _0})\\= mg(3\cos \alpha  - 2\cos {\alpha _0})\end{array}\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}{T_{\max }} = mg(3 - 2\cos {\alpha _0})(VTCB)\\{T_{\min }} = mg\cos {\alpha _0}(VTB)\end{array} \right.\\ \Rightarrow \dfrac{{{T_{\max }}}}{{{T_{\min }}}} = \dfrac{{3 - 2\cos {\alpha _0}}}{{\cos {\alpha _0}}} = 1,02\\ \Rightarrow \cos {\alpha _0} = 0,99 \Rightarrow {\alpha _0} = 0,115(rad)\end{array}\)

Loigiaihay.com