Bài 85 trang 156 SBT toán 8 tập 2

Đề bài

Một hình chóp tứ giác đều \(S.ABCD\) có độ dài cạnh đáy là \(10cm\), chiều cao hình chóp là \(12cm.\)

Tính:

a) Diện tích toàn phần của hình chóp.

b) Thể tích hình chóp.

Lời giải chi tiết

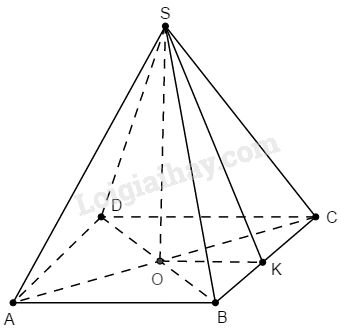
a) Gọi \(O\) là tâm của hình vuông đáy.

Kẻ \(SK ⊥ BC\)

Vì tam giác SBC cân tại S nên SK vừa là đường cao vừa là đường trung tuyến, hay K là trung điểm của BC

Do đó: \(KB = KC =BC:2= 5 \;cm\)

Vì \(SO ⊥ (ABCD)\) nên \(SO ⊥ OK\)

Trong tam giác \(SOK\) có \(\widehat {SOK} = 90^\circ \); \(OK = \displaystyle{1 \over 2}AB = 5\;(cm)\) (vì OK là đường trung bình của tam giác ABC) 

Áp dụng định lí Py-ta-go vào tam giác vuông \(SOK,\) ta có:

\(S{K^2} = S{O^2} + O{K^2} = {12^2} + {5^2} = 169\)

\( \Rightarrow  SK = 13\; (cm)\).

Diện tích xung quanh hình chóp đều là:

\(S_{xq} = \left( {2.10} \right).13 = 260\;(c{m^2})\)

Diện tích mặt đáy là: \(S = 10.10 = 100\;(c{m^2})\)

Diện tích toàn phần hình chóp đều là:

\({S_{TP}} = 260 + 100 = 360\;(c{m^2})\)

b) Thể tích hình chóp đều là:

\(V = \displaystyle {1 \over 3}S.h = \displaystyle {1 \over 3}.100.12 = 400\;(c{m^3})\).

Loigiaihay.com