Giải bài 8 trang 104 SGK Toán 10 tập 2 – Cánh diềuQuan sát hình 64 và thực hiện các hoạt động sau: Quảng cáo
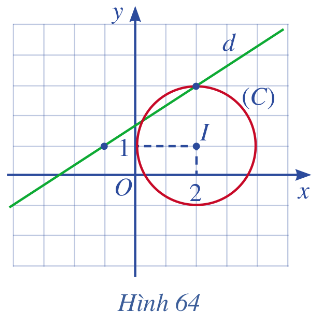
Đề bài Quan sát hình 64 và thực hiện các hoạt động sau: a) Lập phương trình đường thẳng d b) Lập phương trình đường tròn (C) c) Lập phương trình tiếp tuyến của đường tròn \(\left( C \right)\) tại điểm \(M\left( {2 + \sqrt 2 ;1 + \sqrt 2 } \right)\)
Phương pháp giải - Xem chi tiết a) Phương trình đường thẳng d đi qua hai điểm \(A\left( {{x_o};{y_o}} \right);B\left( {{x_1};{y_1}} \right)\) là: \(\frac{{x - {x_o}}}{{{x_1} - {x_o}}} = \frac{{y - {y_o}}}{{{y_1} - {y_o}}}\) b) Đường tròn có tâm \(I\left( {a;b} \right)\) và bán kính R có phương trình là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) c) Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn. Khi đó phương trình tiếp tuyến \(\Delta \) là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\) Lời giải chi tiết a) Đường thẳng d đi qua hai điểm \(\left( { - 1;1} \right)\) và \(\left( {2;3} \right)\) nên phương trình đường thẳng d là: \(\frac{{x + 1}}{{2 + 1}} = \frac{{y - 1}}{{3 - 1}} \Leftrightarrow 2x - 3y + 5 = 0\) b) Phương trình đường tròn (C) có tâm \(I\left( {2;1} \right)\) và \(R = 2\) là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 4\) c) Gọi \({d_1}\) là tiếp tuyến của đường tròn (C) tại điểm \(M\left( {2 + \sqrt 2 ;1 + \sqrt 2 } \right)\) Ta có: \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {IM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Vậy phương trình đường thẳng \({d_1}\) là: \(\sqrt 2 \left( {x - 2 - \sqrt 2 } \right) + \sqrt 2 \left( {y - 1 - \sqrt 2 } \right) = 0 \Leftrightarrow x + y - 3 - 2\sqrt 2 = 0\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
