Giải bài 7.34 trang 43 SGK Toán 7 tập 2 - Kết nối tri thứcTrong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x) Quảng cáo
Đề bài Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x) a) F(x) = 6x4 – 3x3 + 15x2 + 2x – 1 ; G(x) = 3x2 b) F(x) = 12x4 + 10x3 – x – 3 ; G(x) = 3x2 + x + 1 Phương pháp giải - Xem chi tiết +) Muốn chia đa thức A cho đa thức B, ta làm như sau: Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B. Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1 Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3 Bước 5: Làm tương tự như trên Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc. +) Viết A = B. Q + R Lời giải chi tiết a) Thương Q(x) = 2x2 – x + 5 Dư R(x) = 2x – 1 Ta có: F(x) = 3x2 . (2x2 – x + 5) + 2x – 1 b) Thương Q(x) = 4x2 + 2x – 2 Dư R(x) = -x – 1 Ta có: F(x) = (3x2 + x + 1) . (4x2 + 2x – 2) – x – 1
|














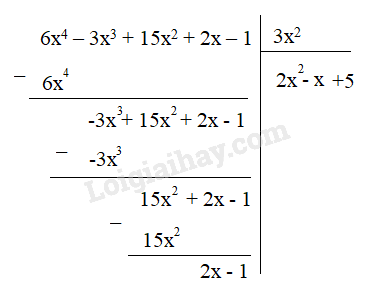
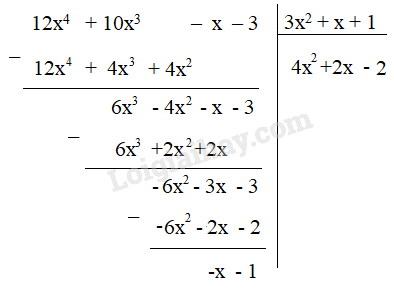






Danh sách bình luận