Đề thi, đề kiểm tra Toán lớp 8 - Cánh diều

Đề thi học kì 2 Toán 8 - Đề số 5 - Cánh diều

Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm (3 điểm) Câu 1: Để giải phương trình $frac{2x-3}{4}-frac{1-x}{5}=1$, một bạn học sinh thực hiện như sau:

Đề bài

I. Trắc nghiệm
Câu 1 :

Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:

Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)

Bước 2: \(10x - 15 - 4 + 4x = 1\)

Bước 3: \(14x - 19 = 1\)

Bước 4: \(14x = 20\)

Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)

Bạn học sinh thực hiện giải như vậy là:

  • A
    Đúng.
  • B
    Sai từ bước 1.
  • C
    Sai từ bước 2.
  • D
    Sai từ bước 3.
Câu 2 :

Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?

  • A
    \(3x - 9 = 0\).
  • B
    \(2x + 6 = 0\).
  • C
    \(2\left( {x - 1} \right) - \left( {3x - 5} \right) = 6 - 2x\).
  • D
    \(\frac{{x - 1}}{2} - 1 = 0\).
Câu 3 :

Phương trình nào sau đây là phương trình bậc nhất một ẩn?

  • A
    \({x^2} - 3 = 0\).
  • B
    \(x + 1 = 0\).
  • C
    \(0x - 7 = 0\).
  • D
    \(\frac{{x\left( {x + 1} \right)}}{x} = 5\).
Câu 4 :

Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là

  • A
    \(S = \left\{ { - 8} \right\}\).
  • B
    \(S = \emptyset \).
  • C
    \(S = \mathbb{R}\).
  • D
    \(S = \left\{ 0 \right\}\).
Câu 5 :

Để x = 1 là nghiệm của phương trình \(2ax - 3a + 1 = 0\) thì giá trị của a là:

  • A
    2.
  • B
    1.
  • C
    -1.
  • D
    -2.
Câu 6 :

theo tỉ số \(\frac{2}{3}\) và $\Delta DEF\backsim \Delta MNP$ theo tỉ số \(\frac{3}{5}\) thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số

  • A
    \(\frac{2}{3}\).
  • B
    \(\frac{3}{5}\)
  • C
    \(\frac{5}{2}\).
  • D
    \(\frac{2}{5}\).
Câu 7 :

Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:

  • A
    \(80c{m^2}\).
  • B
    \(320c{m^2}\).
  • C
    \(640c{m^2}\).
  • D
    \(40c{m^2}\).
Câu 8 :

Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?

  • A
    \(\Delta MED\).
  • B
    \(\Delta MDE\).
  • C
    \(\Delta DEM\).
  • D
    \(\Delta DME\).
Câu 9 :

Cho hình vẽ sau, chọn câu trả lời đúng.

  • A
    $\Delta MPN\backsim \Delta DEF$.
  • B
    $\Delta FDE\backsim \Delta PNM$.
  • C
    $\Delta DEF\backsim \Delta MNP$.
  • D
    $\Delta NMP\backsim \Delta DFE$.
Câu 10 :

Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng

  • A
    \(\frac{1}{2}\).
  • B
    \(\frac{2}{3}\).
  • C
    \(\frac{8}{9}\).
  • D
    \(\frac{5}{6}\).
Câu 11 :

Cho các khẳng định sau:

(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.

(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.

(3) Hai hình thoi bất kì luôn đồng dạng với nhau.

Số khẳng định đúng là:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.
Câu 12 :

Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:

  • A
    \(k = 3\).
  • B
    \(k = 6\).
  • C
    \(k = \frac{1}{2}\).
  • D
    \(k = 2\).
II. Tự luận
Câu 1 :

Giải các phương trình sau:

a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)

b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)

c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
Câu 2 :

Giải bài toán bằng cách lập phương trình

Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 4 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Câu 3 :

Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).

a) Chứng minh $\Delta ABD\backsim \Delta ACB$

b) Tính AD và DC.

c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
Câu 4 :

Giải bài toán bằng cách lập phương trình: (Bài toán cổ Ấn Độ - của nhà toán học Ấn Độ Sridokhara)

Một phần năm đàn ong đậu trên hoa táo, một phần ba đậu trên hoa cúc, số ong đậu trên hoa hồng bằng ba lần hiệu số ong đậu trên hoa táo và hoa cúc. Còn lại một con ong đậu trên hoa mai. Hỏi đàn ong có bao nhiêu con?
Câu 5 :

Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Để giải phương trình \(\frac{{2x - 3}}{4} - \frac{{1 - x}}{5} = 1\), một bạn học sinh thực hiện như sau:

Bước 1: \(\frac{{5\left( {2x - 3} \right)}}{{20}} - \frac{{4\left( {1 - x} \right)}}{{20}} = 1\)

Bước 2: \(10x - 15 - 4 + 4x = 1\)

Bước 3: \(14x - 19 = 1\)

Bước 4: \(14x = 20\)

Bước 5. \(x = \frac{{20}}{{14}} = \frac{{10}}{7}\)

Bạn học sinh thực hiện giải như vậy là:

  • A
    Đúng.
  • B
    Sai từ bước 1.
  • C
    Sai từ bước 2.
  • D
    Sai từ bước 3.

Đáp án : B

Phương pháp giải :

Dựa vào cách giải phương trình bậc nhất một ẩn để kiểm tra.

Lời giải chi tiết :

Bạn học sinh đã thực hiện sai từ bước 1, vì muốn khử mẫu thì cần quy đồng cả hai vế của phương trình mà bạn chỉ quy đồng vế trái.

Đáp án B.

Câu 2 :

Phương trình nào sau đây không có tập nghiệm là \(S = \left\{ 3 \right\}\)?

  • A
    \(3x - 9 = 0\).
  • B
    \(2x + 6 = 0\).
  • C
    \(2\left( {x - 1} \right) - \left( {3x - 5} \right) = 6 - 2x\).
  • D
    \(\frac{{x - 1}}{2} - 1 = 0\).

Đáp án : B

Phương pháp giải :

Giải các phương trình trên để xác định.

Lời giải chi tiết :

\(\begin{array}{l}3x - 9 = 0\\3x = 9\\x = 3\end{array}\)

suy ra tập nghiệm của phương trình A là \(S = \left\{ 3 \right\}\).

\(\begin{array}{l}2x + 6 = 0\\2x =  - 6\\x =  - 3\end{array}\)

suy ra tập nghiệm của phương trình B là \(S = \left\{ { - 3} \right\}\).

\(\begin{array}{l}2\left( {x - 1} \right) - \left( {3x - 5} \right) = 6 - 2x\\2x - 2 - 3x + 5 = 6 - 2x\\2x - 3x + 2x = 6 + 2 - 5\\x = 3\end{array}\)

suy ra tập nghiệm của phương trình C là \(S = \left\{ 3 \right\}\).

\(\frac{{x - 1}}{2} - 1 = 0\)

\(\begin{array}{l}\frac{{x - 1}}{2} - \frac{2}{2} = 0\\x - 1 - 2 = 0\\x = 3\end{array}\)

suy ra tập nghiệm của phương trình D là \(S = \left\{ 3 \right\}\).

Đáp án B.

Câu 3 :

Phương trình nào sau đây là phương trình bậc nhất một ẩn?

  • A
    \({x^2} - 3 = 0\).
  • B
    \(x + 1 = 0\).
  • C
    \(0x - 7 = 0\).
  • D
    \(\frac{{x\left( {x + 1} \right)}}{x} = 5\).

Đáp án : B

Phương pháp giải :

Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\left( {a \ne 0} \right)\).

Lời giải chi tiết :

Phương trình bậc nhất một ẩn là phương trình \(x + 1 = 0\).

Đáp án B.

Câu 4 :

Phương trình \(2x + 7 = 3x + 15\) có tập nghiệm là

  • A
    \(S = \left\{ { - 8} \right\}\).
  • B
    \(S = \emptyset \).
  • C
    \(S = \mathbb{R}\).
  • D
    \(S = \left\{ 0 \right\}\).

Đáp án : A

Phương pháp giải :

Giải phương trình để xác định tập nghiệm

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}2x + 7 = 3x + 15\\2x - 3x = 15 - 7\\ - x = 8\\x =  - 8\end{array}\)

Vậy tập nghiệm của phương trình \(2x + 7 = 3x + 15\) là \(S = \left\{ { - 8} \right\}\).

Đáp án A.

Câu 5 :

Để x = 1 là nghiệm của phương trình \(2ax - 3a + 1 = 0\) thì giá trị của a là:

  • A
    2.
  • B
    1.
  • C
    -1.
  • D
    -2.

Đáp án : B

Phương pháp giải :

Thay x = 1 vào phương trình để tìm a

Lời giải chi tiết :

x = 1 là nghiệm của phương trình \(2ax - 3a + 1 = 0\) nên ta có:

\(\begin{array}{l}2a - 3a + 1 = 0\\ - a =  - 1\\a = 1\end{array}\)

Đáp án B.

Câu 6 :

theo tỉ số \(\frac{2}{3}\) và $\Delta DEF\backsim \Delta MNP$ theo tỉ số \(\frac{3}{5}\) thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số

  • A
    \(\frac{2}{3}\).
  • B
    \(\frac{3}{5}\)
  • C
    \(\frac{5}{2}\).
  • D
    \(\frac{2}{5}\).

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về tam giác đồng dạng.

Lời giải chi tiết :

$\Delta ABC\backsim \Delta DEF$ theo tỉ số \(\frac{2}{3}\) và $\Delta DEF\backsim \Delta MNP$ theo tỉ số \(\frac{3}{5}\) thì $\Delta ABC\backsim \Delta MNP$ theo tỉ số \(\frac{2}{3}.\frac{3}{5} = \frac{2}{5}\) suy ra $\Delta MNP\backsim \Delta ABC$ theo tỉ số \(1:\frac{2}{5} = \frac{5}{2}\).

Đáp án C.

Câu 7 :

Cho $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) và diện tích \(\Delta DEF\) bằng \(160c{m^2}\). Khi đó diện tích \(\Delta ABC\) bằng:

  • A
    \(80c{m^2}\).
  • B
    \(320c{m^2}\).
  • C
    \(640c{m^2}\).
  • D
    \(40c{m^2}\).

Đáp án : D

Phương pháp giải :

Hai tam giác đồng dạng với tỉ số k thì tỉ số diện tích của chúng bằng \({k^2}\).

Lời giải chi tiết :

Vì $\Delta ABC\backsim \Delta DEF$ có \(\frac{{AB}}{{DE}} = \frac{1}{2}\) nên tỉ số đồng dạng của \(\Delta ABC\) với \(\Delta DEF\) là \(\frac{1}{2}\).

Diện tích \(\Delta ABC\) là: \(\frac{1}{{{2^2}}}.160 = \frac{{160}}{4} = 40\left( {c{m^2}} \right)\)

Đáp án D.

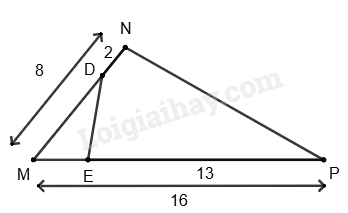
Câu 8 :

Cho \(\Delta MNP\) có MN = 8cm, MP = 16cm. Điểm D thuộc cạnh MN sao cho ND = 2cm, điểm E thuộc cạnh MP sao cho EP = 13cm. Khi đó \(\Delta MNP\) đồng dạng với tam giác nào?

  • A
    \(\Delta MED\).
  • B
    \(\Delta MDE\).
  • C
    \(\Delta DEM\).
  • D
    \(\Delta DME\).

Đáp án : A

Phương pháp giải :

Dựa vào các trường hợp đồng dạng của hai tam giác.

Lời giải chi tiết :

Ta có:

MD = MN – ND = 8 – 2 = 6(cm)

ME = MP – PE = 16 – 13 = 3(cm)

Xét \(\Delta MNP\) và \(\Delta MED\) có:

\(\widehat M\) chung

\(\frac{{ME}}{{MD}} = \frac{{MN}}{{MP}} = \frac{1}{2}\)

Suy ra $\Delta MNP\backsim \Delta MED$ (c.g.c)

Đáp án A.

Câu 9 :

Cho hình vẽ sau, chọn câu trả lời đúng.

  • A
    $\Delta MPN\backsim \Delta DEF$.
  • B
    $\Delta FDE\backsim \Delta PNM$.
  • C
    $\Delta DEF\backsim \Delta MNP$.
  • D
    $\Delta NMP\backsim \Delta DFE$.

Đáp án : C

Phương pháp giải :

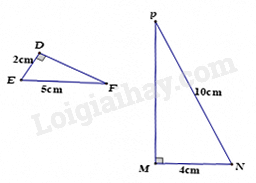
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.

Lời giải chi tiết :

Xét \(\Delta DEF\) và \(\Delta MNP\) có:

\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{2}{4} = \frac{5}{{10}} = \frac{1}{2}} \right)\end{array}\)

nên $\Delta DEF\backsim \Delta MNP$ (cạnh huyền – cạnh góc vuông)

Đáp án C.

Câu 10 :

Cho hình vẽ sau, tỉ số \(\frac{{BE}}{{CE}}\) bằng

  • A
    \(\frac{1}{2}\).
  • B
    \(\frac{2}{3}\).
  • C
    \(\frac{8}{9}\).
  • D
    \(\frac{5}{6}\).

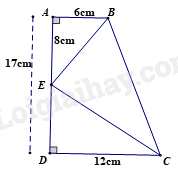
Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm tỉ số.

Lời giải chi tiết :

DE = AD – AE = 17 – 8 = 9(cm)

Xét \(\Delta ABE\) và \(\Delta DEC\) có:

\(\widehat A = \widehat D = {90^0}\)

\(\frac{{AB}}{{DE}} = \frac{{AE}}{{DC}}\left( {\frac{6}{9} = \frac{8}{{12}}\left( { = \frac{2}{3}} \right)} \right)\)

Suy ra $\Delta ABE\backsim \Delta DEC$ (hai cạnh góc vuông) suy ra \(\frac{{BE}}{{CE}} = \frac{{AB}}{{DE}} = \frac{2}{3}\)

Đáp án B.

Câu 11 :

Cho các khẳng định sau:

(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.

(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.

(3) Hai hình thoi bất kì luôn đồng dạng với nhau.

Số khẳng định đúng là:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.

Đáp án : B

Phương pháp giải :

Dựa vào đặc điểm của các hình để xác định.

Lời giải chi tiết :

Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh nên khẳng định (1) đúng.

Hai tam giác cân bất kì luôn đồng dạng là sai vì các góc trong hai tam giác cân có thể khác nhau.

Hai hình thoi bất kì luôn đồng dạng là sai vì các góc trong hai hình thoi có thể khác nhau.

Đáp án B.

Câu 12 :

Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:

  • A
    \(k = 3\).
  • B
    \(k = 6\).
  • C
    \(k = \frac{1}{2}\).
  • D
    \(k = 2\).

Đáp án : D

Phương pháp giải :

Dựa vào bán kính hai đường tròn.

Lời giải chi tiết :

Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: \(\frac{6}{3} = 2\).

Đáp án D.

II. Tự luận
Câu 1 :

Giải các phương trình sau:

a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)

b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)

c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)
Phương pháp giải :

Đưa phương trình về dạng \(ax + b = 0\) để giải.

Lời giải chi tiết :

a) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)

\(\begin{array}{l}7 - 2x - 4 =  - x - 4\\ - 2x + x =  - 4 - 7 + 4\\ - x =  - 7\\x = 7\end{array}\)

Vậy \(x = 7\)

b) \(\frac{{1 - 3x}}{6} + x - 1 = \frac{{x + 2}}{2}\)

\(\begin{array}{l}\frac{{1 - 3x}}{6} + \frac{{6\left( {x - 1} \right)}}{6} = \frac{{3\left( {x + 2} \right)}}{6}\\1 - 3x + 6x - 6 = 3x + 6\\ - 3x + 6x - 3x = 6 + 6 - 1\end{array}\)

\(0 = 11\) (vô lý)

Vậy phương trình vô nghiệm.

c) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\)

\(\begin{array}{l}\frac{{8x - 3}}{4} - \frac{{x + 3}}{4} = \frac{{2x - 1}}{2} + \frac{{3x - 2}}{2}\\\frac{{8x - 3 - x - 3}}{4} = \frac{{2x - 1 + 3x - 2}}{2}\\\frac{{7x - 6}}{4} = \frac{{5x - 3}}{2}\\\frac{{7x - 6}}{4} = \frac{{2\left( {5x - 3} \right)}}{4}\\7x - 6 = 10x - 6\\7x - 10x =  - 6 + 6\\ - 3x = 0\\x = 0\end{array}\)

Vậy \(x = 0\).

Câu 2 :

Giải bài toán bằng cách lập phương trình

Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 4 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Phương pháp giải :

Giải bài toán bằng cách lập phương trình.

Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\)

Biểu diễn số câu trả lời đúng, số câu không trả lời theo x và lập phương trình.

Giải phương trình và kiểm tra nghiệm.

Lời giải chi tiết :

Gọi số câu trả lời không đúng là x \(\left( {x \in N*,x \le 25} \right)\).

Vì số câu trả lời đúng gấp 2 lần số câu trả lời không đúng nên số câu trả lời đúng là \(2x\).

Số câu không trả lời là: \(25 - x - 2x = 25 - 3x\).

Vì học sinh có kết quả đạt 79 điểm nên ta có phương trình:

\(\begin{array}{l}4.2x + 1.\left( {25 - 3x} \right) + 0.x = 79\\12x + 25 - 3x = 79\\9x = 54\\x = 6\left( {TM} \right)\end{array}\)

Khi đó số câu trả lời đúng là: \(2.6 = 12\)(câu)

Số câu không trả lời là: \(25 - 3.6 = 7\)(câu)

Vậy học sinh đó trả lời đúng 12 câu, trả lời không đúng 6 câu và không trả lời 7 câu.

Câu 3 :

Cho \(\Delta ABC\) có \(AB = 2cm,AC = 4cm\). Qua B dựng đường thẳng cắt AC tại D sao cho \(\widehat {ABD} = \widehat {ACB}\).

a) Chứng minh $\Delta ABD\backsim \Delta ACB$

b) Tính AD và DC.

c) Gọi AH là đường cao của \(\Delta ABC\), AE là đường cao của \(\Delta ABD\). Chứng minh rằng diện tích \(\Delta ABH\) gấp 4 lần diện tích \(\Delta ADE\).
Phương pháp giải :

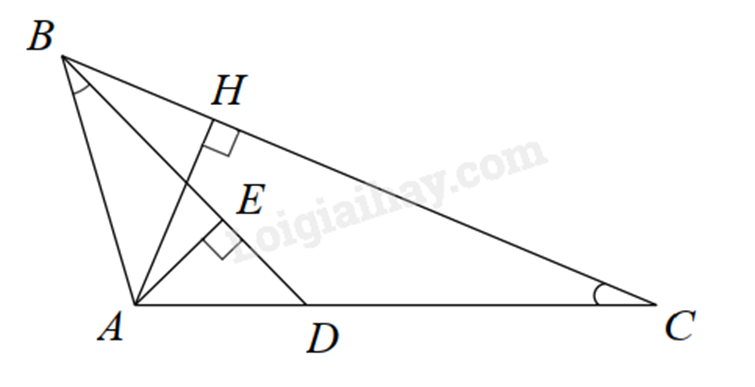
a) Chứng minh $\Delta ABD\backsim \Delta ACB$ theo trường hợp góc – góc.

b) Từ $\Delta ABD\backsim \Delta ACB$ suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{B^2} = AC.AD\), từ đó ta tính AD và DC.

c) Chứng minh $\Delta ADE\backsim \Delta ABH$ theo trường hợp góc – góc suy ra tỉ số đồng dạng giữa các cặp cạnh tương ứng để chứng minh.

Sử dụng công thức tính diện tích tam giác vuông chứng minh.

Lời giải chi tiết :

a) Xét \(\Delta ABD\) và \(\Delta ACB\) có:

\(\widehat {ABD} = \widehat {ACB}\) (gt)

\(\widehat {BAC}\) chung

Suy ra $\Delta ABD\backsim \Delta ACB$ (g.g). (đpcm)

b) Vì $\Delta ABD\backsim \Delta ACB$ (cmt) suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) nên \(A{B^2} = AC.AD\).

Suy ra \({2^2} = 4.AD\) hay \(AD = 1\left( {cm} \right)\).

Suy ra \(CD = AC - AD = 4 - 1 = 3\left( {cm} \right)\)

c) Do $\Delta ABD\backsim \Delta ACB$ suy ra \(\widehat {ADE} = \widehat {ABC}\).

Xét \(\Delta AED\) và \(\Delta AHB\) có:

\(\widehat E = \widehat H = {90^0}\)

\(\widehat {ADE} = \widehat {ABC}\)(cmt)

Suy ra $\Delta ADE\backsim \Delta ABH\left( g.g \right)$ suy ra \(\frac{{AE}}{{AH}} = \frac{{DE}}{{BH}} = \frac{{AD}}{{AB}} = \frac{1}{2}\).

Do đó \(BH = 2DE;AH = 2AE\).

Từ đó suy ra \({S_{\Delta ABH}} = \frac{1}{2}BH.AH = \frac{1}{2}\left( {2DE} \right)\left( {2AE} \right) = 4.\frac{1}{2}DE.AE = 4{S_{\Delta ADE}}\) (đpcm).

Câu 4 :

Giải bài toán bằng cách lập phương trình: (Bài toán cổ Ấn Độ - của nhà toán học Ấn Độ Sridokhara)

Một phần năm đàn ong đậu trên hoa táo, một phần ba đậu trên hoa cúc, số ong đậu trên hoa hồng bằng ba lần hiệu số ong đậu trên hoa táo và hoa cúc. Còn lại một con ong đậu trên hoa mai. Hỏi đàn ong có bao nhiêu con?
Phương pháp giải :

Giải bài toán bằng cách lập phương trình.

Gọi số con ong của đàn ong là x (con) (\(x > 1,x \in N*\))

Lập phương trình dựa vào đề bài

Giải phương trình và kiểm tra nghiệm.

Lời giải chi tiết :

Gọi số con ong của đàn ong là x (con) (\(x > 1,x \in N*\))

Số ong đậu trên hoa táo là \(\frac{1}{5}x\).

Số ong đậu trên hoa cúc là \(\frac{1}{3}x\).

Số ong đậu trên hoa hồng là: \(3\left( {\frac{1}{3}x - \frac{1}{5}x} \right) = 3.\frac{2}{{15}}x = \frac{6}{{15}}x\)

Còn lại một con ong đậu trên hoa mai nên ta có phương trình.

\(x - \frac{1}{5}x - \frac{1}{3}x - \frac{6}{{15}}x = 1\)

Giải phương trình ta được \(x = 15\) (TM)

Vậy đàn ong có 15 con.

Câu 5 :

Giải phương trình \(\frac{{x - 15}}{{17}} + \frac{{x - 36}}{{16}} + \frac{{x - 58}}{{14}} + \frac{{x - 76}}{{12}} = 14\).
Phương pháp giải :

Trừ các 2 vế cho 14 theo cách sau:

\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)

Rút gọn vế trái để giải phương trình.

Lời giải chi tiết :

Trừ các 2 vế cho 14 ta được:

\(\left( {\frac{{x - 15}}{{17}} - 5} \right) + \left( {\frac{{x - 36}}{{16}} - 4} \right) + \left( {\frac{{x - 58}}{{14}} - 3} \right) + \left( {\frac{{x - 76}}{{12}} - 2} \right) = 0\)

\(\begin{array}{l}\frac{{x - 100}}{{17}} + \frac{{x - 100}}{{16}} + \frac{{x - 100}}{{14}} + \frac{{x - 100}}{{12}} = 0\\\left( {x - 100} \right)\left( {\frac{1}{{17}} + \frac{1}{{16}} + \frac{1}{{14}} + \frac{1}{{12}}} \right) = 0\\x - 100 = 0\\x = 100\end{array}\)

Vậy \(x = 100\)

 

Bài liên quan
close