Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Biểu thức thích hợp của đẳng thức \({x^2} + ... + 4{y^2} = {\left( {x + 2y} \right)^2}\) là:
Câu 2 :
Kết quả của phép tính \({72^2} + {22^2} - 44.72\) là:
Câu 3 :
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 15cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Câu 4 :
Tam giác có độ dài ba cạnh trong trường hợp nào sau đây là tam giác vuông?
Câu 6 :
Cho hàm số \(y = f\left( x \right) = \frac{1}{3}x - 1\). Giá trị của \(f\left( { - 3} \right)\) là:
Câu 7 :
Hình chóp tam giác đều có:
Câu 8 :
Xác định các hệ số của \(x\), hệ số tự do của hàm số bậc nhất \(y = - \frac{1}{2}x + 7\).
Câu 9 :
Cho hình chóp tam giác đều có diện tích đáy là \(18c{m^2}\) và chiều cao là \(5cm\). Thể tích của hình chóp tam giác đều là:
Câu 10 :
Kết quả của phép tính \(\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\) là:
Câu 11 :
Mẹ Lan đưa cho Lan 210 000 đồng lên siêu thị gần nhà mua xoài. Biết rằng giá 1 kg xoài là 50 000 đồng. Hãy tính số tiền \(y\) (đồng) còn lại khi mua \(x\) kg xoài và cho biết \(y\) có phải là hàm số của \(x\) hay không?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Biểu thức thích hợp của đẳng thức \({x^2} + ... + 4{y^2} = {\left( {x + 2y} \right)^2}\) là:
Đáp án : B Phương pháp giải :
Sử dụng hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Lời giải chi tiết :
Ta có: \({\left( {x + 2y} \right)^2} = {x^2} + 2.x.2y + 4{y^2} = {x^2} + 4xy + 4{y^2}\) nên biểu thức còn thiếu là \(4xy\). Đáp án B
Câu 2 :
Kết quả của phép tính \({72^2} + {22^2} - 44.72\) là:
Đáp án : C Phương pháp giải :
Sử dụng hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}{72^2} + {22^2} - 44.72\\ = {72^2} - 2.22.72 + {22^2}\\ = {\left( {72 - 22} \right)^2}\\ = {50^2} = 2500\end{array}\) Đáp án C
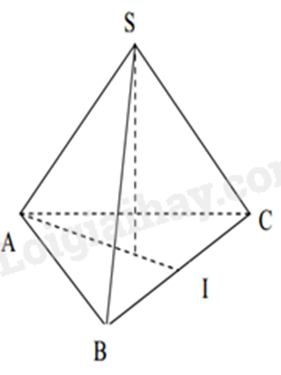
Câu 3 :
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 15cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
Đáp án : B Phương pháp giải :
Diện tích xung quanh của hình chóp tứ giác đều bằng nửa chu vi đáy nhân chiều cao. Lời giải chi tiết :
Diện tích xung quanh của hình chóp tứ giác đều đó là: \({S_{xq}} = \frac{1}{2}.\left( {8.4} \right).15 = 240\left( {c{m^2}} \right)\) Đáp án B
Câu 4 :
Tam giác có độ dài ba cạnh trong trường hợp nào sau đây là tam giác vuông?
Đáp án : D Phương pháp giải :
Áp dụng định lí Pythagore đảo: nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trong tam giác thì tam giác là tam giác vuông. Lời giải chi tiết :
\({9^2} + {6^2} = 81 + 36 = 117 \ne 100 = {10^2}\) nên 10cm, 6cm, 9cm không phải độ dài ba cạnh của một tam giác vuông. \({3^2} + {4^2} = 9 + 16 = 25 \ne 36 = {6^2}\) nên 3 cm, 4 cm, 6 cm không phải độ dài ba cạnh của một tam giác vuông. \({6^2} + {8^2} = 36 + 64 = 100 \ne 121 = {11^2}\) nên 11cm, 6cm, 8cm không phải độ dài ba cạnh của một tam giác vuông. \({12^2} + {35^2} = 144 + 1225 = 1369 = {37^2}\) nên 12cm, 35cm, 37cm là độ dài ba cạnh của một tam giác vuông. Đáp án D
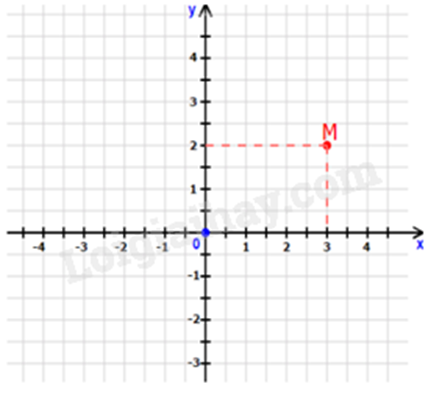
Đáp án : A Phương pháp giải :
Quan sát mặt phẳng tọa độ, xác định tọa độ điểm \(M\left( {{x_M};{y_M}} \right)\). Lời giải chi tiết :
Tọa độ điểm M trên mặt phẳng tọa độ là \(M\left( {3;2} \right)\). Đáp án A
Câu 6 :
Cho hàm số \(y = f\left( x \right) = \frac{1}{3}x - 1\). Giá trị của \(f\left( { - 3} \right)\) là:
Đáp án : B Phương pháp giải :
Thay \(x = - 3\) vào hàm số \(y = f\left( x \right)\) để tính giá trị. Lời giải chi tiết :
Giá trị của \(f\left( { - 3} \right)\) là: \(y = f\left( { - 3} \right) = \frac{1}{3}.\left( { - 3} \right) - 1 = - 1 - 1 = - 2\). Đáp án B
Câu 7 :
Hình chóp tam giác đều có:
Đáp án : D Phương pháp giải :
Dựa vào đặc điểm của hình chóp tam giác đều.
Lời giải chi tiết :
Hình chóp tam giác đều có 4 mặt (3 mặt bên, 1 mặt đáy) và 6 cạnh. Đáp án D
Câu 8 :
Xác định các hệ số của \(x\), hệ số tự do của hàm số bậc nhất \(y = - \frac{1}{2}x + 7\).
Đáp án : B Phương pháp giải :
Hàm số bậc nhất \(y = ax + b\) có hệ số của \(x\) là \(a\) và hệ số tự do là \(b\). Lời giải chi tiết :
Hàm số bậc nhất \(y = - \frac{1}{2}x + 7\) có hệ số của \(x\) là \( - \frac{1}{2}\) và hệ số tự do là \(7\). Đáp án B
Câu 9 :
Cho hình chóp tam giác đều có diện tích đáy là \(18c{m^2}\) và chiều cao là \(5cm\). Thể tích của hình chóp tam giác đều là:
Đáp án : C Phương pháp giải :
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) diện tích đáy nhân chiều cao: V = \(\frac{1}{3}\)Sđáy.h. Lời giải chi tiết :
Thể tích của hình chóp tam giác đều là: \(V = \frac{1}{3}.18.5 = 30\left( {c{m^3}} \right)\). Đáp án C
Câu 10 :
Kết quả của phép tính \(\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\) là:
Đáp án : C Phương pháp giải :
Áp dụng quy tắc chia đa thức cho đơn thức: ta chia lần lượt các hạng tử của đa thức cho đơn thức. Lời giải chi tiết :
Ta có: \(\begin{array}{l}\left( {8{x^9}{y^2} - 6{x^6}{y^3} + {x^3}{y^4}} \right):2{x^3}{y^2}\\ = 8{x^9}{y^2}:2{x^3}{y^2} - 6{x^6}{y^3}:2{x^3}{y^2} + {x^3}{y^4}:2{x^3}{y^2}\\ = 4{x^6} - 3{x^3}y + \frac{1}{2}{y^2}\end{array}\) Đáp án C
Câu 11 :
Mẹ Lan đưa cho Lan 210 000 đồng lên siêu thị gần nhà mua xoài. Biết rằng giá 1 kg xoài là 50 000 đồng. Hãy tính số tiền \(y\) (đồng) còn lại khi mua \(x\) kg xoài và cho biết \(y\) có phải là hàm số của \(x\) hay không?
Đáp án : A Phương pháp giải :
Biểu diễn số tiền \(y\) theo \(x\) dựa vào đề bài. Xác định xem \(y\) có phải là hàm số của \(x\) hay không Lời giải chi tiết :
Số tiền bạn Lan mua \(x\) kg xoài là: \(50\,000.x\) (đồng) Số tiền \(y\) còn lại khi mua \(x\) kg xoài là: \(y = 210\,000 - 50\,000x\). Khi đó \(y\) là hàm số của \(x\). Đáp án A
Đáp án : B Phương pháp giải :
Dựa vào dấu hiệu nhận biết hình thang cân. Lời giải chi tiết :
Hình thang có hai đường chéo bằng nhau là hình thang cân. Đáp án B
II. Tự luận
Phương pháp giải :
Áp dụng phương pháp sử dụng hằng đẳng thức để phân tích đa thức thành nhân tử. a) Sử dụng hằng đẳng thức hiệu hai bình phương. b) Sử dụng hằng đẳng thức bình phương của một hiệu, sau đó sử dụng hằng đẳng thức hiệu hai bình phương. Lời giải chi tiết :
a) \({x^2} - 9 = \left( {x - 3} \right)\left( {x + 3} \right)\) b) \({x^2} - 4x + 4 - {y^2}\) \(\begin{array}{l} = \left( {{x^2} - 4x + 4} \right) - {y^2}\\ = {\left( {x - 2} \right)^2} - {y^2}\\ = \left( {x - 2 - y} \right)\left( {x - 2 + y} \right)\end{array}\) Phương pháp giải :
a) Thay \(x = 2\) vào A để tính giá trị. b) Quy đồng mẫu để rút gọn biểu thức B. c) Tính \(P = A.B\), Sử dụng kiến thức về ước và bội, dấu hiệu chia hết để biện luận giá trị biểu thức là số nguyên. Lời giải chi tiết :
a) Thay \(x = 2\) (thỏa mãn điều kiện) vào A, ta được: \(A = \frac{{2.2 - 3}}{{2 - 1}} = \frac{1}{1} = 1\). b) Ta có: \(\begin{array}{l}B = \frac{x}{{x - 1}} + \frac{3}{{x + 1}} - \frac{{6x - 4}}{{{x^2} - 1}}\\ = \frac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \frac{{3\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} - \frac{{6x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + x + 3x - 3 - 6x + 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} + \left( {x + 3x - 6x} \right) + \left( { - 3 + 4} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{x^2} - 2x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\\ = \frac{{x - 1}}{{x + 1}}\end{array}\) Vậy \(B = \frac{{x - 1}}{{x + 1}}\). c) Ta có: \(\begin{array}{l}P = A.B = \frac{{2x - 3}}{{x - 1}}.\frac{{x - 1}}{{x + 1}} = \frac{{2x - 3}}{{x + 1}}\\ = \frac{{2x + 2 - 5}}{{x + 1}} = \frac{{2\left( {x + 1} \right) - 5}}{{x + 1}} = 2 - \frac{5}{{x + 1}}\end{array}\) Để P nguyên thì \(2 - \frac{5}{{x + 1}}\) nguyên, suy ra \(\frac{5}{{x + 1}}\) nguyên. \(\frac{5}{{x + 1}}\) nguyên khi \(5 \vdots \left( {x + 1} \right)\) hay \(\left( {x + 1} \right) \in \) Ư(5) = \(\left\{ { \pm 1; \pm 5} \right\}\). Ta có bảng giá trị sau:
Vì \(x\) là số nguyên dương nên \(x = 4\) thỏa mãn. Vậy biểu thức \(P = A.B\) nhận giá trị là số nguyên khi \(x = 4\). Phương pháp giải :
a) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ. b) Áp dụng công thức tính thời gian hoàn thành = tổng số sản phẩm làm được : số sản phẩm làm được trong 1 giờ. Thời gian hoàn thành sớm hơn dự kiến = thời gian dự kiến – thời gian hoàn thành thực tế. Lời giải chi tiết :
a) Biểu thức biểu thị thời gian dự kiến người công nhân đó hoàn thành kế hoạch là: \(\frac{{120}}{x}\) (giờ) b) Trong 2 giờ công nhân sản xuất với năng suất dự kiến, người công nhân làm được: \(2x\) (sản phẩm). Khi đó số sản phẩm còn lại là \(120 - 2x\) (sản phẩm) Sau khi tăng năng suất thì mỗi giờ công nhân sản xuất được: \(x + 3\) sản phẩm. Người đó sản xuất \(120 - 2x\) trong thời gian là: \(\frac{{120 - 2x}}{{x + 3}}\) (giờ) Biểu thức biểu thị thời gian thực tế công nhân đó hoàn thành số sản phẩm là: \(2 + \frac{{120 - 2x}}{{x + 3}}\) (giờ) Vậy biểu thức biểu thị thời gian công nhân đó hoàn thành kế hoạch sớm hơn thời gian dự kiến là: \(\begin{array}{l}\frac{{120}}{x} - \left( {2 + \frac{{120 - 2x}}{{x + 3}}} \right)\\ = \frac{{120}}{x} - 2 - \frac{{120 - 2x}}{{x + 3}}\\ = \frac{{120\left( {x + 3} \right) - 2x\left( {x + 3} \right) - x\left( {120 - 2x} \right)}}{{x\left( {x + 3} \right)}}\\ = \frac{{120x + 360 - 2{x^2} - 6x - 120x + 2{x^2}}}{{x\left( {x + 3} \right)}}\\ = \frac{{360 - 6x}}{{x\left( {x + 3} \right)}}\end{array}\) Phương pháp giải :
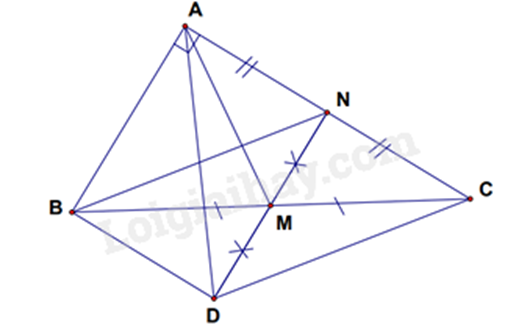
a) Chứng minh BDCN có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành. b) Chứng minh ABDN là hình chữ nhật nên hai đường chéo AD và BN bằng nhau. c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền để tính BC. Áp dụng định lí Pythagore để tính AB. Tính diện tích tam giác vuông bằng \(\frac{1}{2}\) tích hai cạnh góc vuông. Lời giải chi tiết :
a) Xét tứ giác BNCD có: M là giao điểm của BC và DN M là trung điểm của BC (gt) M là trung điểm của ND (gt) Suy ra BNCD là hình bình hành. b) Vì tứ giác BNCD là hình bình hành nên BD // CN, BD = CN. Mà AN = NC (vì N là trung điểm của AC) nên BD // AN; BD = AN. Xét tứ giác ABDN có: BD // AN; BD = AN Suy ra ABDN là hình bình hành. Mà \(\widehat {BAN} = 90^\circ \) nên ABDN là hình chữ nhật. Suy ra AD = BN c) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AN là đường trung tuyến ứng với cạnh huyền nên \(AM = \frac{1}{2}BC\), suy ra \(BC = 2AM = 2.5 = 10\left( {cm} \right)\). Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có: \(A{B^2} = B{C^2} - A{C^2} = {10^2} - {8^2} = 100 - 64 = 36\) suy ra \(AB = \sqrt {36} = 6\left( {cm} \right)\). Vậy diện tích tam giác ABC là: \({S_{\Delta ABC}} = \frac{1}{2}.AB.AC = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\) Phương pháp giải :
Biến đổi đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\) bằng cách nhân hai vế với 2. Sử dụng hằng đẳng thức bình phương của một tổng, bình phương của một hiệu để giải tìm x, y. Thay vào M để tính giá trị của M. Lời giải chi tiết :
Nhân hai vế của đẳng thức \(\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1 = 0\) với 2, ta được: \(\begin{array}{l}2\left( {\frac{1}{2}{x^2} + 2{y^2} - x + 2y + 1} \right) = 0\\{x^2} + 4{y^2} - 2x + 4y + 2 = 0\\\left( {{x^2} - 2x + 1} \right) + \left( {4{y^2} + 4y + 1} \right) = 0\\{\left( {x - 1} \right)^2} + {\left( {2y + 1} \right)^2} = 0\end{array}\) Vì \({\left( {x - 1} \right)^2} \ge 0\) với mọi x, \({\left( {2y + 1} \right)^2} \ge 0\) với mọi y. Để \({\left( {x - 1} \right)^2} + {\left( {2y + 1} \right)^2} = 0\) thì \(x - 1 = 0\) và \(2y + 1 = 0\), suy ra \(x = 1\) và \(y = \frac{{ - 1}}{2}\). Thay vào M, ta được: \(\begin{array}{l}M = {\left[ {1 + 2.\left( {\frac{{ - 1}}{2}} \right)} \right]^{2022}} + {\left( {1 - 2} \right)^{2023}} + {\left( { - \frac{1}{2} + \frac{3}{2}} \right)^{2024}}\\ = {\left( {1 - 1} \right)^{2022}} + {\left( { - 1} \right)^{2023}} + {1^{2024}}\\ = 0 - 1 + 1 = 0\end{array}\)
|

























Danh sách bình luận