Đề thi học kì 1 Toán 8 - Đề số 2 - Cánh diềuTổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức $2{{x}^{4}}y-4{{y}^{5}}+5{{x}^{4}}y-7{{y}^{5}}+{{x}^{2}}{{y}^{2}}-2{{x}^{4}}y$ ta được:Đề bài
I. Trắc nghiệm
Câu 1 :
Thu gọn đa thức \(2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\) ta được:
Câu 2 :
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức nào?
Câu 3 :
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \) b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\) c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\) 1. \(\frac{{x - y}}{{x + y}}\) 2. \(\frac{{ - 3}}{{x - y}}\) 3. x2 + 4x + 4
Câu 4 :
Hình thang cân là hình thang
Câu 5 :
Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì thì AEDF là chữ nhật?
Câu 6 :
Cho tam giác ABC vuông tại A có AB = \(\frac{1}{2}\)BC, đường trung tuyến AM. Tam giác ABM là tam giác gì?
Câu 7 :
Cho hình chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm như hình bên dưới, hình nào là hình khai triển của hình chóp tam giác đều đã cho?
Câu 8 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
Câu 9 :
Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình thoi có độ dài là:
Câu 10 :
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
Câu 11 :
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
Câu 12 :
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (kg) thanh long ruột đỏ loại I là :
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Thu gọn đa thức \(2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\) ta được:
Đáp án : D Phương pháp giải :
Sử dụng quy tắc tính với đa thức. Lời giải chi tiết :
Ta có: \(\begin{array}{l}2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\\ = \left( {2{x^4}y + 5{x^4}y - 2{x^4}y} \right) + \left( { - 4{y^5} - 7{y^5}} \right) + {x^2}{y^2}\\ = 5{x^4}y - 11{y^5} + {x^2}{y^2}\end{array}\)
Câu 2 :
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức nào?
Đáp án : D Phương pháp giải :
Dựa vào quy tắc chia đa thức cho đơn thức. Đa thức chia hết cho một đơn thức nếu các hạng tử của đa thức đó chia hết cho đơn thức. Vì vậy bậc của các biến đơn thức phải không lớn hơn bậc của các biến trong đa thức. Lời giải chi tiết :
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) là đa thức biến x với bậc nhỏ nhất của biến x là 2 nên A, B, C không thỏa mãn. (4xy có biến y; 6x3 có bậc của x là 3; x5 có bậc của x là 5). Vậy đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức 4x2.
Câu 3 :
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng. a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \) b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\) c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\) 1. \(\frac{{x - y}}{{x + y}}\) 2. \(\frac{{ - 3}}{{x - y}}\) 3. x2 + 4x + 4 Đáp án
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \) 3. x2 + 4x + 4 b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\) 1. \(\frac{{x - y}}{{x + y}}\) c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\) 2. \(\frac{{ - 3}}{{x - y}}\) Phương pháp giải :
Sử dụng kiến thức về phân thức đại số. Lời giải chi tiết :
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \frac{{{{\left( {x + 2} \right)}^3}}}{{x + 2}} = {\left( {x + 2} \right)^2} = {x^2} + 4x + 4\) nên a – 3. b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\) là: \(1:\frac{{x + y}}{{x - y}} = \frac{{x - y}}{{x + y}}\) nên b – 1. c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\) là: \( - \left( {\frac{3}{{x - y}}} \right) = \frac{{ - 3}}{{x - y}}\) nên c – 2. Đáp án: a – 3; b – 1; c – 2.
Câu 4 :
Hình thang cân là hình thang
Đáp án : D Phương pháp giải :
Sử dụng khái niệm hình thang cân. Lời giải chi tiết :
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Câu 5 :
Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì thì AEDF là chữ nhật?
Đáp án : B Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình vuông. Lời giải chi tiết :
Vì DE // AF; DF // AE (gt) => AEDF là hình bình hành. Để hình bình hành AEDF là hình chữ nhật thì \(\widehat A = {90^0}\) hay tam giác ABC vuông tại A.
Câu 6 :
Cho tam giác ABC vuông tại A có AB = \(\frac{1}{2}\)BC, đường trung tuyến AM. Tam giác ABM là tam giác gì?
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông. Lời giải chi tiết :
Ta có tam giác ABC vuông tại A, AM là đường trung tuyến nên AM = \(\frac{1}{2}\)BC = BM = MC. Mà AB = \(\frac{1}{2}\)BC (gt) => AM = AB = BM hay tam giác ABM đều.
Câu 7 :
Cho hình chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm như hình bên dưới, hình nào là hình khai triển của hình chóp tam giác đều đã cho?
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hình chóp tam giác đều. Lời giải chi tiết :
Hình khai triển của chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm là hình b.
Câu 8 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
Đáp án : A Phương pháp giải :
Dựa vào công thức tính thể tích hình chóp tứ giác. Lời giải chi tiết :
Thể tích hình chóp S.ABCD là: \(V = \frac{1}{3}{S_d}.h = \frac{1}{3}{3^2}.2 = 6\left( {c{m^3}} \right)\).
Câu 9 :
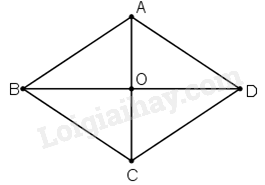
Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình thoi có độ dài là:
Đáp án : B Phương pháp giải :
Sử dụng định lí Pythagore để tính. Lời giải chi tiết :
Xét hình thoi ABCD có AC = 8cm; BD = 10cm nên AO = 4 cm và OD = 5cm. Áp dụng định lí Pythagore vào tam giác vuông OAD, ta có: \(AD = \sqrt {O{A^2} + O{D^2}} = \sqrt {{4^2} + {5^2}} = \sqrt {41} \left( {cm} \right)\)
Câu 10 :
Cho hàm số \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\) .
Đáp án : C Phương pháp giải :
Thay x = -5; x = 5 vào hàm số. Tính \(f\left( { - 5} \right) + f\left( 5 \right)\). Lời giải chi tiết :
Ta có: \(\begin{array}{l}f\left( { - 5} \right) = {\left( { - 5} \right)^2} = 25\\f\left( 5 \right) = {5^2} = 25\\ \Rightarrow f\left( { - 5} \right) + f\left( 5 \right) = 25 + 25 = 50\end{array}\)
Câu 11 :
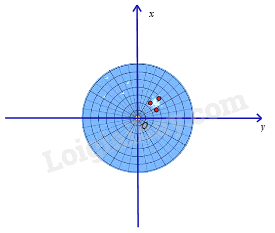
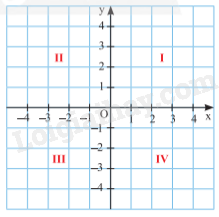
Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về các góc phần tư.
Lời giải chi tiết :
Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ I.
Câu 12 :
Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (kg) thanh long ruột đỏ loại I là :
Đáp án : C Phương pháp giải :
Biểu thị y theo x. Lời giải chi tiết :
Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng nên giá bán x (kg) thanh long là: 32 000.x (đồng). Vậy ta có công thức biểu thị là y = 32 000x.
Đáp án : D Phương pháp giải :
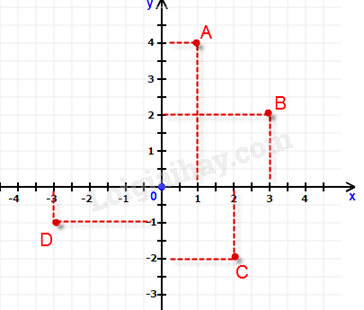
Quan sát hình vẽ để xác định tọa độ các điểm. Lời giải chi tiết :
Hình chiếu của điểm A trên trục hoành là 1, trên trục tung là 4 nên tọa độ điểm A là A(1; 4). => A đúng. Hình chiếu của điểm B trên trục hoành là 3, trên trục tung là 2 nên tọa độ điểm B là B(3; 2). => B đúng. Hình chiếu của điểm C trên trục hoành là 2, trên trục tung là -2 nên tọa độ điểm C là C(2;-2). => C đúng. Hình chiếu của điểm D trên trục hoành là -3, trên trục tung là -1 nên tọa độ điểm D là C(-3;-1). => D sai.
II. Tự luận
Phương pháp giải :
a) Kiểm tra điều kiện của mẫu thức. b) Rút gọn biểu thức A. c) Thay x = 10 để tính giá trị biểu thức. d) Để biểu thức A nguyên thì mẫu thức phải là ước của tử thức. Lời giải chi tiết :
a) Điều kiện xác định của biểu thức A là: \(\left\{ \begin{array}{l}x + 4 \ne 0\\x - 4 \ne 0\\{x^2} - 16 \ne 0\end{array} \right. \\ suy \; ra \left\{ \begin{array}{l}x \ne - 4\\x \ne 4\end{array} \right.\) Vậy điều kiện xác định của biểu thức A là \(x \ne \pm 4\). b) Ta có: \(\begin{array}{l}A = \frac{1}{{x + 4}} + \frac{x}{{x - 4}} + \frac{{24 - {x^2}}}{{{x^2} - 16}}\\ = \frac{{x - 4}}{{\left( {x + 4} \right)\left( {x - 4} \right)}} + \frac{{x\left( {x + 4} \right)}}{{\left( {x + 4} \right)\left( {x - 4} \right)}} + \frac{{24 - {x^2}}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{x - 4 + {x^2} + 4x + 24 - {x^2}}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{5x + 20}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{5\left( {x + 4} \right)}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{5}{{x - 4}}\end{array}\) c) Tại x = 10 (thỏa mãn điều kiện xác định), ta được: \(A = \frac{5}{{10 - 4}} = \frac{5}{6}\). d) Biểu thức A nguyên thì \( \frac{5}{{x - 4}}\) nguyên. \(\frac{5}{{x - 4}}\) nguyên khi và chỉ khi \(\left( {x - 4} \right) \in Ư\left( 5 \right) = \left\{ { \pm 1; \pm 5} \right\}\). Ta có bảng giá trị sau:
Vậy các số nguyên x để giá trị của biểu thức A là số nguyên là 3; 5; -1; 9. Phương pháp giải :
Dựa vào các phép tính với đa thức, các hằng đẳng thức để rút gọn A. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}A = \left( {x + 5} \right)\left( {x + 1} \right) + \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) - x\left( {{x^2} + x - 2} \right)\\ = \left( {{x^2} + 5x + x + 5} \right) + \left( {{x^3} - {2^3}} \right) - \left( {{x^3} + {x^2} - 2x} \right)\\ = {x^2} + 6x + 5 + {x^3} - 8 - {x^3} - {x^2} + 2x\\ = \left( {{x^3} - {x^3}} \right) + \left( {{x^2} - {x^2}} \right) + \left( {6x + 2x} \right) + \left( {5 - 8} \right)\\ = 8x - 3\end{array}\) b) 742 + 242 – 48.74 = 742 + 242 – 2.24.74 = (74 – 24)2 = 502 = 2 500. Phương pháp giải :
Dựa vào biểu đồ để trả lời câu hỏi. Lời giải chi tiết :
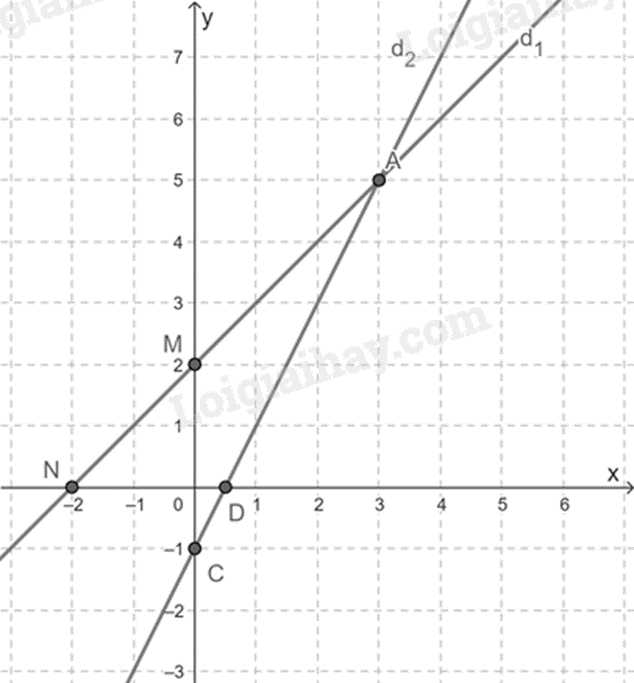
a) Vẽ đồ thị: * y = 2x - 1: Cho \(x = 0 \Rightarrow y = - 1\) có C(0; -1) Cho \(y = 0 \Rightarrow x = \frac{1}{2}\) có D(\(\frac{1}{2};0\)) Đường thẳng CD là đồ thị hàm số y = 2x – 1. * y = x + 2: Cho \(x = 0 \Rightarrow y = 2\) có M(0; 2) Cho \(y = 0 \Rightarrow x = - 2\) có N(-2; 0) Đường thẳng MN là đồ thị hàm số y = x + 2 Ta được đường thẳng \({d_1};{d_2}\) .
b) Tìm tọa độ của điểm A: Ta có phương trình hoành độ giao điểm: 2x – 1 = x + 2 \( \Leftrightarrow \) 2x – x = 2 + 1 \( \Leftrightarrow \) x = 3. Với x = 3; y = 2.3 – 1 = 5 => A(3; 5). Vậy tọa độ của điểm A(3; 5). c) Vì đồ thị hàm số \({d_3}\) song song với \({d_1}\) nên a = 2 và b \( \ne \) -1. => \({d_3}\): y = 2x + b. Vì đồ thị hàm số \({d_3}\) cắt đường thẳng \({d_2}\) tại B có hoành độ bằng -1 nên tung độ của điểm B là y = -1 + 2 = 1. => B(-1;1) . Vì B thuộc đồ thị hàm số \({d_3}\) nên thay tọa độ của điểm B vào hàm số y = 2x + b, ta được: 1 = 2.(-1) + b => b = 3 (thỏa mãn). => Hàm số cần tìm là y = 2x + 3. Phương pháp giải :
1. Dựa vào định lí Pythagore để tính. 2. a) Tứ giác AKCM là hình chữ nhật. b) Chứng minh AKMB có hai cạnh đối song song và bằng nhau. c) AKCM là hình vuông thì các cạnh phải bằng nhau. Lời giải chi tiết :
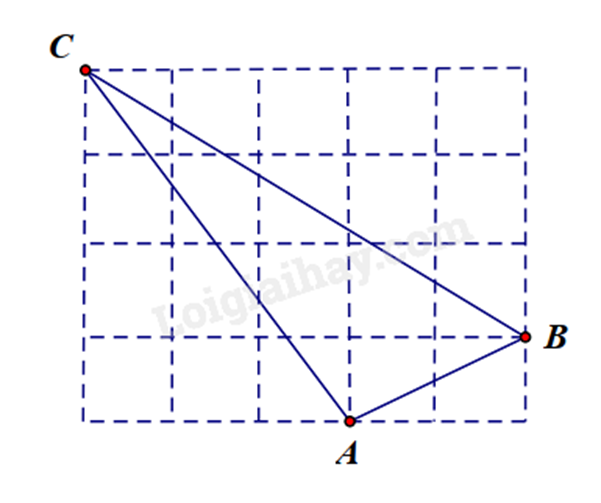
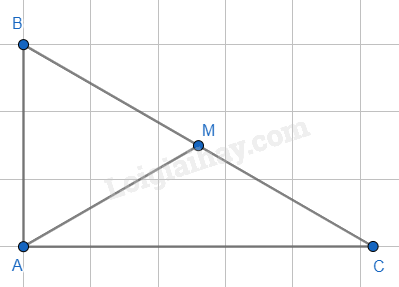
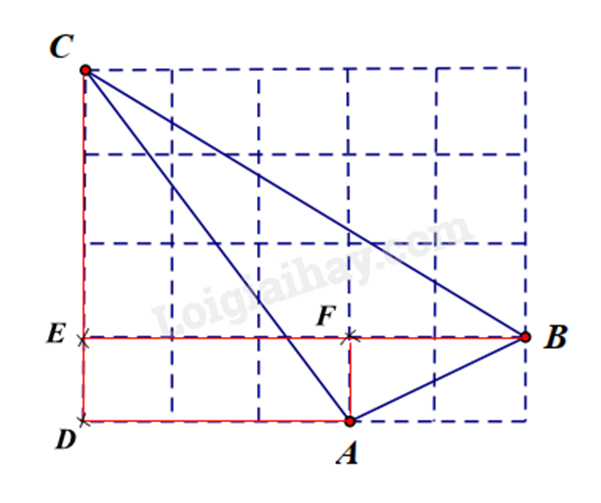
1.
Gọi các điểm D, E và F như trên hình vẽ. Khi đó ta có các tam giác vuông ACD vuông tại D; BCE vuông tại E và ABF vuông tại F. Tam giác ACD có AD = 3cm; CD = 4cm. Áp dụng định lí Pythagore vào tam giác ADC, ta có: \(\begin{array}{l}A{C^2} = A{D^2} + C{D^2} = {3^2} + {4^2} = 25\\ \Rightarrow AC = 5cm\end{array}\) Tam giác BCE có BE = 5cm; CE = 3cm. Áp dụng định lí Pythagore vào tam giác BCE, ta có: \(\begin{array}{l}B{C^2} = B{E^2} + C{E^2} = {5^2} + {3^2} = 34\\ \Rightarrow BC = \sqrt {34} cm\end{array}\) Tam giác ABF có AF = 1cm; BF = 2cm. Áp dụng định lí Pythagore vào tam giác ABF, ta có: \(\begin{array}{l}A{B^2} = A{F^2} + F{B^2} = {1^2} + {2^2} = 5\\ \Rightarrow AB = \sqrt 5 cm\end{array}\) 2.
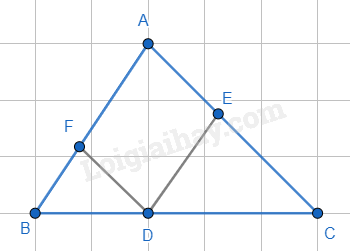
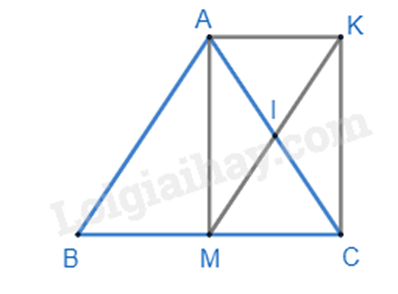
a) Xét tứ giác AKCM có: I là trung điểm của AC; I là trung điểm của KM (vì M đối xứng với K qua I) => AKCM là hình bình hành. Xét tam giác ABC cân tại A có M là trung điểm của BC nên AM là đường trung tuyến đồng thời là đường cao của tam giác ABC. => \(\widehat {AMC} = {90^0}\). Hình bình hành AKCM có \(\widehat {AMC} = {90^0}\) nên là hình chữ nhật. b) Ta có AKCM là hình chữ nhật nên AK // CM và AK = CM. Mà BM = CM nên BM = AK và BM // AK. => Tứ giác AKMB là hình bình hành. c) Để AKCM là hình chữ nhật thì AM = MC = \(\frac{1}{2}\) Mà AM là đường trung tuyến của tam giác ABC nên khi đó AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC hay tam giác ABC vuông tại A. Phương pháp giải :
Sử dụng hằng đẳng thức để biến đổi biểu thức. Lời giải chi tiết :
\(\begin{array}{l}A = - {x^2} + \frac{2}{3}x - 1\\ = - \left( {{x^2} - 2x.\frac{1}{3} + \frac{1}{9} - \frac{1}{9} + 1} \right)\\ = - \left[ {{x^2} - 2x.\frac{1}{3} + {{\left( {\frac{1}{3}} \right)}^2} + \frac{8}{9}} \right]\\ = - \left[ {{{\left( {x - \frac{1}{3}} \right)}^2} + \frac{8}{9}} \right] = - {\left( {x - \frac{1}{3}} \right)^2} - \frac{8}{9}\end{array}\) Ta có \( - {\left( {x - \frac{1}{3}} \right)^2} \le 0\) nên \( - {\left( {x - \frac{1}{3}} \right)^2} - \frac{8}{9} < 0\) với mọi x. Vậy A < 0 hay luôn luôn âm với mọi giá trị x.
|
























Danh sách bình luận