Đề thi giữa kì 2 Toán 8 - Đề số 1 - Cánh diềuPhần trắc nghiệm (3 điểm) Câu 1: (149308) Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau:Đề bài
I. Trắc nghiệm
Câu 1 :
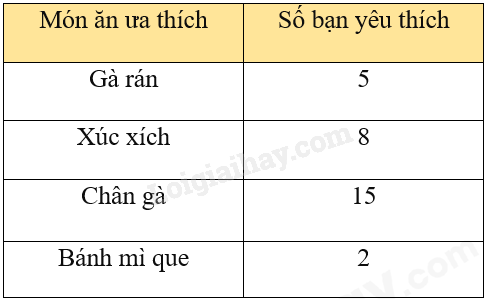
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :
Dữ liệu định lượng (số liệu) trong bảng là :
Câu 2 :
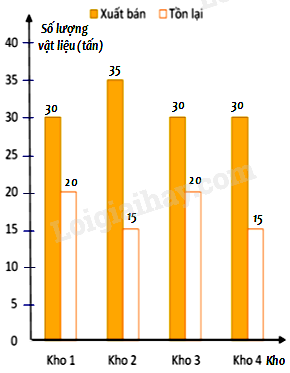
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?
Câu 3 :
Số ô tô có được của 4 xã trong một huyện năm 2022 được thống kê trong bảng sau:
Xã có nhiều ô tô nhất trong năm 2022 chiếm bao nhiêu % tổng 4 xã?
Câu 4 :
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 3” là thẻ
Câu 5 :
Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa, 7 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt ngửa xuất hiện” là:
Câu 6 :
Lớp 8C có 40 học sinh trong đó có 16 nữ. Lớp phó lao động chọn một bạn để trực nhật trong một buổi học. Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp” là
Câu 7 :
Cho AB = 16cm. CD = 3dm. Tỉ số \(\frac{{AB}}{{CD}}\) là:
Câu 10 :
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
Câu 11 :
Có bao nhiêu đường trung bình trong một tam giác?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Các món ăn yêu thích của học sinh lớp 8A ghi lại trong bảng sau :
Dữ liệu định lượng (số liệu) trong bảng là :
Đáp án : B Phương pháp giải :
Dựa vào phân loại dữ liệu: Dữ liệu được chia thành hai loại: Dữ liệu định tính (dữ liệu không phải số) và dữ liệu định lượng (số liệu). Lời giải chi tiết :
Dữ liệu định lượng (số liệu) trong bảng trên là dữ liệu Số bạn yêu thích : 5; 8; 15; 2.
Câu 2 :
Một công ty kinh doanh vật liệu xây dựng có bốn kho hàng có 50 tấn hàng. Kế toán của công ty lập biểu đồ cột kép ở hình bên biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong mỗi kho sau tuần lễ kinh doanh đầu tiên. Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép đó. Theo em, kế toán đã ghi nhầm số liệu ở kho nào ?
Đáp án : D Phương pháp giải :
Kiểm tra xem dữ liệu trong biểu đồ có cột nào chưa chính xác. Lời giải chi tiết :
Vì mỗi kho hàng đều có 50 tấn hàng nên tổng số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại phải bằng 50 tấn. Mà cột kho 4, số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại là: 30 + 15 = 45 (tấn) nên số liệu ở kho 4 không đúng.
Câu 3 :
Số ô tô có được của 4 xã trong một huyện năm 2022 được thống kê trong bảng sau:
Xã có nhiều ô tô nhất trong năm 2022 chiếm bao nhiêu % tổng 4 xã?
Đáp án : A Phương pháp giải :
Tính số ô tô của 4 xã, xã có ô tô nhiều nhất. Tính số phần trăm số ô tô của xã D so với số ô tô của tổng 4 xã. Lời giải chi tiết :
Xã có nhiều ô tô nhất năm 2022 là xã D (20 ô tô) Tổng số ô tô của 4 xã là: 15 + 10 + 15 + 20 = 60 (ô tô) Số ô tô của xã D chiếm số phần trăm tổng 4 xã là: \(\frac{{20}}{{60}} = \frac{1}{3} \approx 33,3\% \).
Câu 4 :
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 3” là thẻ
Đáp án : A Phương pháp giải :
Liệt kê các thẻ có số ghi trên thẻ chia hết cho 3. Lời giải chi tiết :
Trong 4 tấm thẻ chỉ có thẻ ghi số 3 là kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 3”.
Câu 5 :
Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa, 7 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt ngửa xuất hiện” là:
Đáp án : A Phương pháp giải :
Xác suất thực nghiệm của biến cố “Mặt ngửa xuất hiện” bằng tỉ số giữa số lần xuất hiện mặt ngửa với tổng số lần tung. Lời giải chi tiết :
Xác suất thực nghiệm của biến cố “Mặt ngửa xuất hiện” là: \(\frac{{13}}{{20}}\).
Câu 6 :
Lớp 8C có 40 học sinh trong đó có 16 nữ. Lớp phó lao động chọn một bạn để trực nhật trong một buổi học. Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp” là
Đáp án : A Phương pháp giải :
Tính số học sinh nam trong lớp Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp” bẳng tỉ số giữa số bạn nam trong lớp với tổng số học sinh. Lời giải chi tiết :
Số học sinh nam trong lớp là: 40 – 16 = 24 (học sinh). Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp” là \(\frac{{24}}{{40}} = 0,6\).
Câu 7 :
Cho AB = 16cm. CD = 3dm. Tỉ số \(\frac{{AB}}{{CD}}\) là:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tỉ số giữa hai đoạn thẳng. Lời giải chi tiết :
Đổi 3dm = 30cm. Tỉ số \(\frac{{AB}}{{CD}} = \frac{{16}}{{30}} = \frac{8}{{15}}\).
Đáp án : C Phương pháp giải :
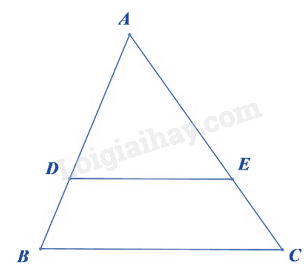
Dựa vào định lí Thales đảo trong tam giác. Lời giải chi tiết :
Theo định lí đảo trong tam giác, nếu \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}} \Rightarrow DE//BC\).
Đáp án : A Phương pháp giải :
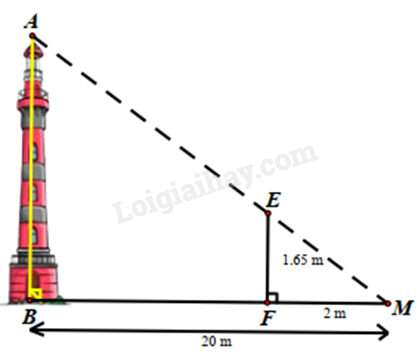
Dựa vào hệ quả của định lí Thales để tính AB. Lời giải chi tiết :
Vì EF // AB nên \(\frac{{AB}}{{EF}} = \frac{{BM}}{{MF}}\)\( \Rightarrow AB = \frac{{BM.EF}}{{MF}} = \frac{{20.1,65}}{2} = 16,5\left( m \right)\)
Câu 10 :
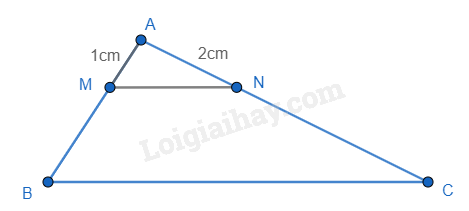
Cho tam giác ABC, vẽ MN//BC sao cho AN =\(\frac{1}{2}\)AB, M \( \in \) AB, N \( \in \) AC. Biết AN = 2cm, AM = 1cm, thì AC bằng:
Đáp án : C Phương pháp giải :
Áp dụng định lí Thalès để tính BC. Lời giải chi tiết :
Vì AN = \(\frac{1}{2}\)AB nên AB = 2.AN = 2.2 = 4(cm). Ta có MN // BC. Áp dụng định lí Thales, ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Leftrightarrow \frac{1}{4} = \frac{2}{{AC}} \Leftrightarrow AC = 4.2 = 8\) (cm). Vậy AC = 8cm.
Câu 11 :
Có bao nhiêu đường trung bình trong một tam giác?
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đường trung bình. Lời giải chi tiết :
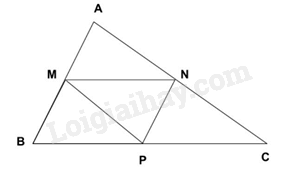
Xét tam giác ABC bất kì. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
MN là đường trung bình của tam giác ABC. NP là đường trung bình của tam giác ABC. MP là đường trung bình của tam giác ABC. Vậy có 3 đường trung bình trong một tam giác.
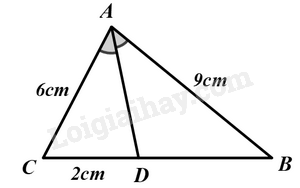
Đáp án : D Phương pháp giải :
Sử dụng tính chất của đường phân giác trong tam giác. Lời giải chi tiết :
Ta có AD là tia phân giác của góc A nên \(\frac{{AB}}{{BD}} = \frac{{AC}}{{CD}} \Leftrightarrow \frac{9}{{BD}} = \frac{6}{2} = 3\) \( \Rightarrow BD = \frac{9}{3} = 3\)(cm)
II. Tự luận
Phương pháp giải :
Liệt kê các kết quả thuận lợi cho biến cố. Xác xuất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho tổng số kết quả có thể. Lời giải chi tiết :
Số kết quả có thể xảy ra khi rút ngẫu nhiên một tấm thẻ từ trong hộp là 10 kết quả. a) Số kết quả thuận lợi cho biến cố A: “Rút được tấm thẻ ghi số là số nhỏ hơn 15” là 4 kết quả (11; 12; 13; 14) Xác suất của biến cố A: “Rút được tấm thẻ ghi số là số nhỏ hơn 15” là: \(P\left( A \right) = \frac{4}{{10}} = \frac{2}{5}\). b) Số kết quả thuận lợi cho biến cố B: “Rút được tấm thẻ ghi số là bội của 3” là 3 kết quả (12; 15; 18) Xác suất của biến cố B: “Rút được tấm thẻ ghi số là bội của 3” là: \(P\left( B \right) = \frac{3}{{10}}\). c) Số kết quả thuận lợi cho biến cố C: “Rút được tấm thẻ ghi số nguyên tố” là 4 kết quả (11; 13; 17; 19) Xác suất của biến cố C: “Rút được tấm thẻ ghi số nguyên tố” là: \(P\left( C \right) = \frac{4}{{10}} = \frac{2}{5}\). Phương pháp giải :
a) Dựa vào dữ liệu đề bài cho để điền vào bảng. b) Điền số tương ứng vào biểu đồ. Lời giải chi tiết :
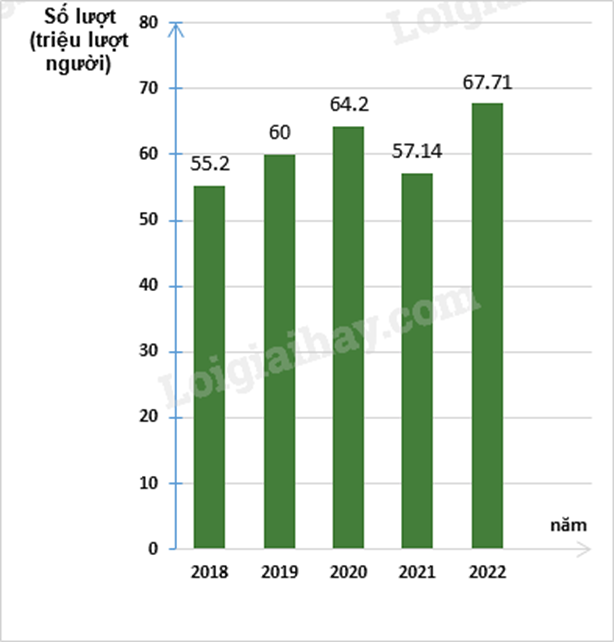
a) Ta có bảng thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm:
b) Biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên là: Phương pháp giải :
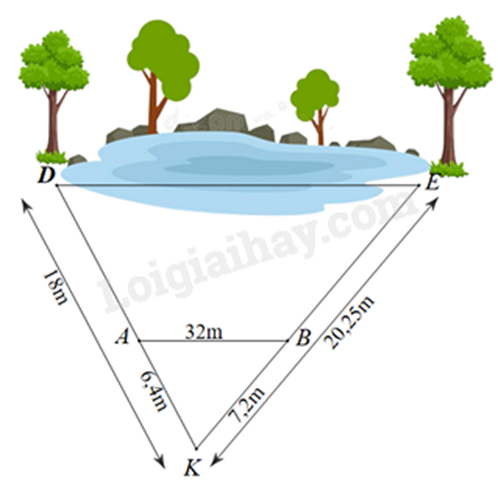
a) Dựa vào tỉ số hai đoạn thẳng để chứng minh. b) Dựa vào định lí Thales đảo để chứng minh. c) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa AB và DE để tính DE. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}\frac{{KB}}{{KE}} = \frac{{7,2}}{{20,25}} = \frac{{16}}{{45}}\\\frac{{KA}}{{KD}} = \frac{{6,4}}{{18}} = \frac{{16}}{{45}}\end{array}\) suy ra \( \frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (đpcm) b) Vì \(\frac{{KB}}{{KE}} = \frac{{KA}}{{KD}}\) (cmt) nên AB // DE (Định lí Thales đảo trong tam giác) c) Vì AB // DE nên ta có: \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{KA}}{{KD}} = \frac{{16}}{{45}}\\\frac{{32}}{{DE}} = \frac{{16}}{{45}}\\ DE = 32:\frac{{16}}{{45}} = 90\left( m \right)\end{array}\) Vậy khoảng cách giữa D và E là 90m. Phương pháp giải :
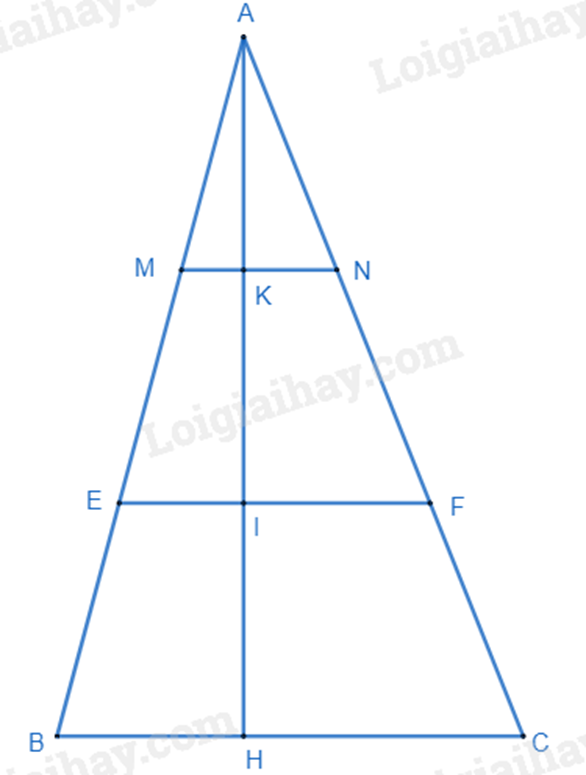
a) Áp dụng hệ quả của định lí Thales để suy ra tỉ số giữa MN, EF với BC. b) Tính độ dài AH qua công thức tính diện tích tam giác. Từ đó suy ra AK. Chứng minh MNFE là hình thang, KI là đường cao của hình thang MNFE. Sử dụng công thức tính diện tích hình thang. Lời giải chi tiết :
a) Theo bài ra ta có \(AK = KI = IH\)\( \Rightarrow \frac{{AK}}{{AH}} = \frac{1}{3};\frac{{AI}}{{AH}} = \frac{2}{3}\). Áp dụng hệ quả của định lí Thales vào tam giác ABH có MK // BH và EI // BH \( \Rightarrow \frac{{MK}}{{BH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{EI}}{{BH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (1) Áp dụng hệ quả của định lí Thales vào tam giác ACH có NK // CH và FI // CH \( \Rightarrow \frac{{NK}}{{CH}} = \frac{{AK}}{{AH}} = \frac{1}{3}\); \(\frac{{FI}}{{CH}} = \frac{{AI}}{{AH}} = \frac{2}{3}\) (2) Từ (1) và (2), áp dụng dãy tỉ số bằng nhau ta có: \(\frac{{MK}}{{BH}} = \frac{{NK}}{{CH}} = \frac{{MK + NK}}{{BH + CH}} = \frac{{MN}}{{BC}} = \frac{1}{3}\)\( \Rightarrow MN = \frac{1}{3}BC = \frac{{20}}{3}\left( {cm} \right)\) \(\frac{{EI}}{{BH}} = \frac{{FI}}{{CH}} = \frac{{EI + FI}}{{BH + CH}} = \frac{{EF}}{{BC}} = \frac{2}{3}\)\( \Rightarrow EF = \frac{2}{3}BC = \frac{2}{3}.20 = \frac{{40}}{3}\left( {cm} \right)\) b) Diện tích tam giác ABC là \(300c{m^2}\) \(\begin{array}{l} \Rightarrow \frac{1}{2}AH.BC = 300\\\frac{1}{2}AH.20 = 300\\ \Rightarrow AH = 300:\frac{{20}}{2} = 30\left( {cm} \right)\end{array}\) Ta có: \(\frac{{AK}}{{AH}} = \frac{1}{3} \Rightarrow AK = \frac{1}{3}AH = \frac{1}{3}.30 = 10\left( {cm} \right)\) \( \Rightarrow \) KI = AK = 10 cm. Vì MN và EF cùng song song với BC nên MNFE là hình thang. Vì \(AH \bot BC \Rightarrow AH \bot MN\) và \(AH \bot EF\) \( \Rightarrow KI\) là đường cao của hình thang MNFE \(\left( {K \in MN;I \in EF} \right)\). Diện tích hình thang MNFE là: \({S_{MNFE}} = \frac{1}{2}\left( {MN + EF} \right).KI = \frac{1}{2}.\left( {\frac{{20}}{3} + \frac{{40}}{3}} \right).10 = 100\left( {c{m^2}} \right)\) Vậy \({S_{MNFE}} = 100c{m^2}\). Phương pháp giải :
Tính số học sinh nam. Xác suất thực nghiệm của biến cố “Gặp một học sinh nam của lớp” bẳng tỉ số học sinh nam trên tổng số học sinh của lớp. Lời giải chi tiết :
Số học sinh nam của lớp là: \(60\% .40 = 24\) (học sinh). Xác suất thực nghiệm của biến cố “Gặp một học sinh nam của lớp” là: \(\frac{{24}}{{40}} = \frac{3}{5}\).
|















 b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.
b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.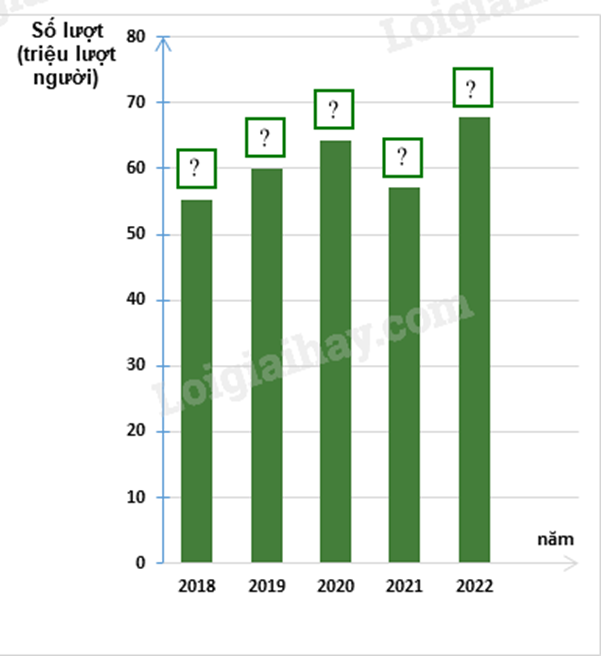








Danh sách bình luận