Đề thi học kì 1 Toán 7 - Đề số 14 - Kết nối tri thứcI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.Đề bài
I. Trắc nghiệm
Câu 2 :
Cho các số \(\frac{2}{{ - 5}};\,\frac{{ - 3}}{{ - 4}} ;\,\frac{5}{7};\,\sqrt 2 ;\,\frac{{ - 9}}{{11}}\). Các số hữu tỉ dương là:
Câu 3 :
Cho biểu thức \({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2}\). Kết quả phép tính ở dạng lũy thừa là:
Câu 4 :
Cho 2 số thực a và b với \(a > 0\) và \(b < 0\). Giá trị tuyệt đối của tích a.b là:
Câu 5 :
Khi thực hiện phép tính \(\sqrt {{3^2} + {4^2}} \). Biến đổi đúng là:
Câu 6 :
Cho các số: \(\frac{2}{3};\,\frac{{ - 3}}{5};\,\frac{7}{{20}};\,\frac{5}{{22}};\,\frac{1}{{ - 8}};\,\frac{\pi }{2}\). Các số viết được dưới dạng số thập phân hữu hạn là:
Câu 7 :
Làm tròn số 75647 với độ chính xác \(d = 50\). Kết quả là:
Câu 9 :
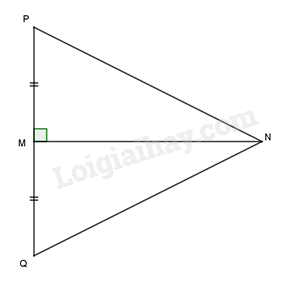
Cho \(\Delta MNP\) và \(\Delta MNQ\) có \(MP = MQ\), \(\widehat {PMN} = \widehat {QMN} = 90^\circ \). Cần bổ sung thêm điều kiện nào để hai tam giác bằng nhau?
Câu 10 :
Cho \(\Delta ABC\) có \(\widehat A = 70^\circ ;\widehat B = 55^\circ \). Ta có
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Đáp án : C Phương pháp giải :
Dựa vào cách biểu diễn số hữu tỉ trên trục số. Lời giải chi tiết :
Điểm A nằm bên trái số 0 nên A là số hữu tỉ âm. Ta thấy từ -1 đến 0 được chia làm 3 phần bằng nhau nên mẫu số bằng 3. Điểm A chiếm hai phần về phía chiều âm trục số nên tử số bằng -2. Vậy số hữu tỉ A = \( - \frac{2}{3}\)
Câu 2 :
Cho các số \(\frac{2}{{ - 5}};\,\frac{{ - 3}}{{ - 4}} ;\,\frac{5}{7};\,\sqrt 2 ;\,\frac{{ - 9}}{{11}}\). Các số hữu tỉ dương là:
Đáp án : D Phương pháp giải :
Số hữu tỉ dương là số lớn hơn 0. Lời giải chi tiết :
Ta có: \(\begin{array}{l}\frac{2}{{ - 5}} = \frac{{ - 2}}{5} < 0\\\frac{{ - 3}}{{ - 4}} = \frac{3}{4} > 0\\\frac{5}{7} > 0\end{array}\) \(\sqrt 2 \) không phải là số hữu tỉ. \(\frac{{ - 9}}{{11}} < 0\) Vậy chỉ có \(\frac{{ - 3}}{{ - 4}};\frac{5}{7}\) là số hữu tỉ dương.
Câu 3 :
Cho biểu thức \({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2}\). Kết quả phép tính ở dạng lũy thừa là:
Đáp án : A Phương pháp giải :
Biến đổi biểu thức về phép chia hai lũy thừa cùng cơ số. Lời giải chi tiết :
Ta có: \({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2} = {\left( {\frac{{ - 2}}{3}} \right)^6}:{\left[ {{{\left( {\frac{{ - 2}}{3}} \right)}^2}} \right]^2} = {\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{{ - 2}}{3}} \right)^4} = {\left( {\frac{{ - 2}}{3}} \right)^{6 - 4}} = {\left( {\frac{{ - 2}}{3}} \right)^2} = {\left( {\frac{2}{3}} \right)^2}\).
Câu 4 :
Cho 2 số thực a và b với \(a > 0\) và \(b < 0\). Giá trị tuyệt đối của tích a.b là:
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa giá trị tuyệt đối của một số: \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\). Lời giải chi tiết :
Vì a > 0 và b < 0 nên tích a.b < 0. Khi đó giá trị tuyệt đối của tích a.b là: \(\left| {ab} \right| = - \left( {ab} \right) = - ab\).
Câu 5 :
Khi thực hiện phép tính \(\sqrt {{3^2} + {4^2}} \). Biến đổi đúng là:
Đáp án : A Phương pháp giải :
Tính phép tính trong căn bậc hai. Lời giải chi tiết :
Ta có: \(\sqrt {{3^2} + {4^2}} = \sqrt {9 + 16} = \sqrt {25} \).
Câu 6 :
Cho các số: \(\frac{2}{3};\,\frac{{ - 3}}{5};\,\frac{7}{{20}};\,\frac{5}{{22}};\,\frac{1}{{ - 8}};\,\frac{\pi }{2}\). Các số viết được dưới dạng số thập phân hữu hạn là:
Đáp án : C Phương pháp giải :
Các phân số tối giản với mẫu số dương mà mẫu chỉ có ước nguyên tố là 2 và 5 đều viết được dưới dạng số thập phân hữu hạn. Lời giải chi tiết :
Trong các số hữu tỉ trên, chỉ có \(\frac{{ - 3}}{5};\frac{7}{{20}};\frac{1}{{ - 8}}\) có mẫu số chỉ có ước nguyên tố là 2 và 5 nên các số này là số thập phân hữu hạn. Đặc biệt, số \(\frac{\pi }{2}\) có mẫu số bằng 2 nhưng tử số là số thập phân vô hạn không tuần hoàn nên \(\frac{\pi }{2}\) không phải là số thập phân hữu hạn.
Câu 7 :
Làm tròn số 75647 với độ chính xác \(d = 50\). Kết quả là:
Đáp án : C Phương pháp giải :
Dựa vào cách làm tròn số với độ chính xác cho trước. Lời giải chi tiết :
Làm tròn số 75647 với độ chính xác 50 tức là làm tròn số 75647 đến hàng trăm. Số 75647 đến hàng trăm làm tròn đến hàng trăm ta được số 75 600.
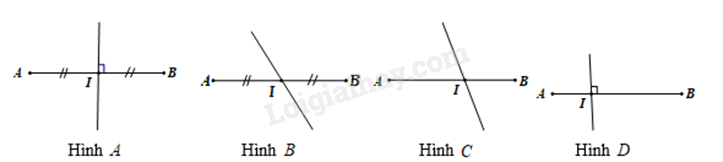
Đáp án : A Phương pháp giải :
Dựa vào khái niệm đường trung trực của một đoạn thẳng. Lời giải chi tiết :
Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Câu 9 :
Cho \(\Delta MNP\) và \(\Delta MNQ\) có \(MP = MQ\), \(\widehat {PMN} = \widehat {QMN} = 90^\circ \). Cần bổ sung thêm điều kiện nào để hai tam giác bằng nhau?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết hai tam giác vuông bằng nhau. Lời giải chi tiết :
Hai \(\Delta MNP\) và \(\Delta MNQ\) có \(MP = MQ\), \(\widehat {PMN} = \widehat {QMN} = 90^\circ \) và cạnh \(MN\) chung nên \(\Delta MNP = \Delta MNQ\) (hai cạnh góc vuông) Do vậy không cần bổ sung điều kiện.
Câu 10 :
Cho \(\Delta ABC\) có \(\widehat A = 70^\circ ;\widehat B = 55^\circ \). Ta có
Đáp án : A Phương pháp giải :
Dựa vào định lí tổng ba góc trong một tam giác bằng 1800 và dấu hiệu nhận biết một tam giác cân. Lời giải chi tiết :
Số đo góc C là: \(\widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {70^0} - {55^0} = {55^0}\). Vì tam giác ABC có \(\widehat B = \widehat C = {55^0}\) nên tam giác ABC cân tại A.
Đáp án : B Phương pháp giải :
Dựa vào dấu hiệu nhận biết tia phân giác Lời giải chi tiết :
Ta có tia AF nằm AB và Ax, \(\widehat {BAF} = \widehat {FAx}\) nên AF là tia phân giác của góc BAx.
Đáp án : D Phương pháp giải :
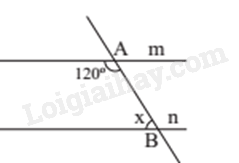
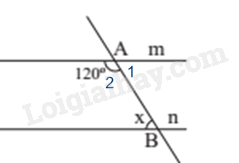
Dựa vào tính chất hai góc kề bù và hai góc so le trong của hai đường thẳng song song. Lời giải chi tiết :
Ta có góc A1 và góc A2 là hai góc kề bù nên số đo góc A1 là: \({180^0} - \widehat {{A_2}} = {180^0} - {120^0} = {60^0}\). Vì m // n nên \(\widehat {{A_1}} = x = {60^0}\) (hai góc so le trong)
II. Tự luận
Phương pháp giải :
- Sử dụng tính chất của phép nhân. - Sử dụng định nghĩa giá trị tuyệt đối của một số: \(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\). Lời giải chi tiết :
a) \(\frac{{ - 7}}{5}.\left( {\frac{{15}}{{14}} + \frac{5}{7}} \right) + \left| {\frac{{ - 7}}{2}} \right|\) \(\begin{array}{l} = \frac{{ - 7}}{5}.\frac{{15}}{{14}} + \left( {\frac{{ - 7}}{5}} \right).\frac{5}{7} + \frac{7}{2}\\ = \frac{{ - 3}}{2} + \left( { - 1} \right) + \frac{7}{2} = \left( {\frac{{ - 3}}{2} + \frac{7}{2}} \right) - 1 = 2 - 1 = 1\end{array}\) b) \(\frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {{{\left( {\frac{3}{5}} \right)}^2} - \frac{{\sqrt {25} }}{{18}} + \frac{{19}}{{11}}} \right]\) \(\begin{array}{l} = \frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {\frac{9}{{25}} - \frac{5}{{18}} + \frac{{19}}{{11}}} \right]\\ = \frac{1}{{13}} - \frac{5}{{18}} - \frac{1}{{13}} + \frac{9}{{25}} - \frac{9}{{25}} + \frac{5}{{18}} + \frac{{19}}{{11}}\\ = \left( {\frac{1}{{13}} - \frac{1}{{13}}} \right) + \left( {\frac{5}{{18}} - \frac{5}{{18}}} \right) + \left( {\frac{9}{{25}} - \frac{9}{{25}}} \right) + \frac{{19}}{{11}}\\ = \frac{{19}}{{11}}\end{array}\) Phương pháp giải :
Tính số tiền lãi ông Newton nhận được khi hết thời hạn một năm. Tính lãi suất ngân hàng. Lời giải chi tiết :
Số tiền lãi ông Newton nhận được khi hết thời hạn một năm là: \(534 - 500 = 34\)(triệu đồng) Lãi suất ngân hàng là: \(\frac{{34}}{{500}}.100\% = 6,8\% \) Phương pháp giải :
Tính tổng số điểm của lớp 7A. Tính tổng số học sinh lớp 7A. Điểm thi trung bình của lớp 7A bằng tổng số điểm chia cho tổng số học sinh. Lời giải chi tiết :
Tổng điểm lớp 7A: \(S = 4.1 + 5.2 + 6.5 + 7.6 + 8.7 + 9.10 + 10.4 = 272\) Số học sinh lớp 7A: \(N = 1 + 2 + 5 + 6 + 7 + 10 + 4 = 35\) Điểm trung bình môn Toán của lớp 7A là: \(\overline X = \frac{S}{N} = \frac{{272}}{{35}} \approx 7,8\) Phương pháp giải :
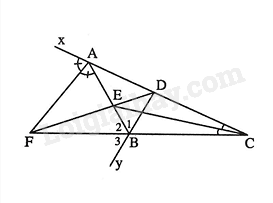
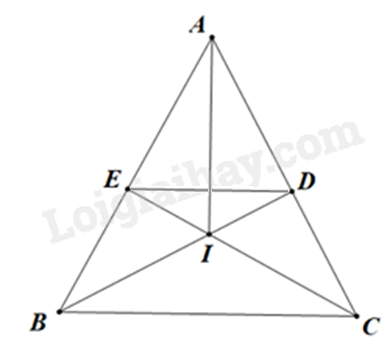
a) Chứng minh AD = AE nên tam giác ADE cân. b) Chứng minh \(\widehat {AED} = \widehat {ABC}\) (hai góc đồng vị) nên DE // BC. c) Chứng minh tam giác BIC cân tại I nên IB = IC. d) Chứng minh A và I cùng thuộc đường trung trực của BC nên \(AI \bot BC\). Lời giải chi tiết :
a) Xét \(\Delta ADB\)và \(\Delta AEC\), có: \(\widehat A\): chung \(AB = AC\)(vì \(\Delta ABC\)cân tại \(A\)) \(\widehat {ADB} = \widehat {AEC} = 90^\circ \)(vì \(BD \bot AC\)tại \(D\), \(CE \bot AB\) tại \(E\)) Suy ra \(\Delta ADB = \Delta ACE\)(cạnh huyền-góc nhọn). Suy ra\(AD = AE\)(2 cạnh tương ứng). Vậy \(\Delta ADE\)cân tại \(A\). b) Vì \(\Delta ABC\)cân tại \(A\) (gt) Ta có: \(\widehat {ABC} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}\) (1) Lại có: \(\Delta AED\) cân tại \(A\) (câu a) Nên \(\widehat {AED} = \frac{{{{180}^{\rm{o}}} - \widehat A}}{2}\) (2) Từ (1) và (2) \( \Rightarrow \widehat {AED} = \widehat {ABC}\) Mà \(\widehat {AED}\) và \(\widehat {ABC}\) ở vị trí đồng vị. Vậy \(DE//BC\). c) Có tia \(BD\) nằm giữa hai tia \(BA,BC\). Suy ra \(\widehat {ABD} + \widehat {DBC} = \widehat {ABC}\) Suy ra \(\widehat {DBC} = \widehat {ABC} - \widehat {ABD}\) Tương tự, có: \(\widehat {ECB} = \widehat {ACB} - \widehat {ACE}\) Mà \(\widehat {ABC} = \widehat {ACB}\) (do \(\Delta ABC\)cân tại \(A\)) \(\widehat {ADB} = \widehat {ACE}\) (vì \(\Delta ADB = \Delta AEC\)) Suy ra \(\widehat {DBC} = \widehat {ECB}\) Vậy \(\Delta IBC\) cân tại \(I\). Suy ra \(IB = IC\) d) Có: \(AB = AC\) (vì \(\Delta ABC\)cân tại \(A\)) Do đó\(A\) thuộc đường trung trực của \(BC\) Lại có: \(IB = IC\)(câu c) Suy ra \(I\) thuộc đường trung trực của \(BC\) Suy ra \(AI\) là đường trung trực của \(BC\) Suy ra \(AI \bot BC\). Phương pháp giải :
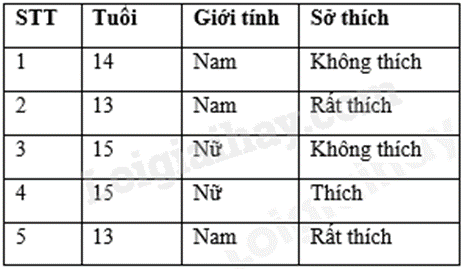
Dữ liệu định tính là dữ liệu không phải là số. Dữ liệu định lượng là dữ liệu số. Độ tuổi trung bình bằng tổng số tuổi chia cho số lượng người. Lời giải chi tiết :
- Dữ liệu định tính: Giới tính, sở thích. - Dữ liệu định lượng: Tuổi. - Độ tuổi trung bình: \(\frac{{14 + 13.2 + 15.2}}{5} = 14\) tuổi
|

























Danh sách bình luận