Đề thi học kì 1 Toán 7 - Đề số 11 - Kết nối tri thứcI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.Đề bài
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Khẳng định nào sau đây sai:
Câu 2 :
Số đối của \(\frac{5}{6}\) là:
Câu 3 :
Căn bậc hai số học của 196 là:
Câu 4 :
Số nào là số vô tỉ trong các số sau:
Câu 5 :
Cho \(\widehat {{\rm{xOy}}} = {70^0}\)và tia Ot là tia phân giác của \(\widehat {{\rm{xOy}}}\). Số đo \(\widehat {{\rm{xOt}}}\) bằng:
Câu 6 :
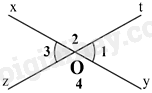
Cho hình vẽ bên, biết \({\widehat {\rm{O}}_1} = {60^0}\). Số đo \({\widehat {\rm{O}}_3}\) là:
Câu 7 :
Đường trung trực của một đoạn thẳng là
Câu 8 :
Cho hai tam giác \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat B = \widehat P\), \(BC = PN\). Cần thêm điều kiện nào để \(\Delta ABC = \Delta MPN\) theo trường hợp góc – cạnh – góc
Câu 9 :
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu định lượng?
Câu 10 :
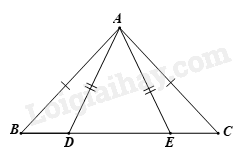
Cho hình vẽ sau có \(\widehat B = {48^O},\widehat {AED} = {65^O}\). Số đo \(\widehat {BAD}\) bằng
Câu 11 :
Kết quả tìm hiểu về sở thích chơi game của một số học sinh trong một trường THCS được ghi bởi bảng thống kê sau. Hãy cho biết nhiều học sinh lựa chọn loại nào nhất?
Câu 12 :
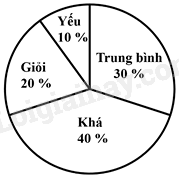
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) xếp loại học lực giữa kì I của học sinh lớp 7A. Hỏi học sinh đạt loại gì là nhiều nhất?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Khẳng định nào sau đây sai:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về số hữu tỉ. Lời giải chi tiết :
+) \(0,\left( {001} \right) = \frac{1}{{999}} \in \mathbb{Q}\) nên A đúng. +) \(\frac{7}{{33}} \in \mathbb{Q}\) nên B đúng. +) \( - {\rm{ }}2\frac{3}{5} = - \frac{{13}}{5} \in \mathbb{Q}\) nên C đúng. +) \(\sqrt 8 \) là số vô tỉ \( \Rightarrow \sqrt 8 \notin \mathbb{Q}\) nên D sai.
Câu 2 :
Số đối của \(\frac{5}{6}\) là:
Đáp án : D Phương pháp giải :
Dựa vào khái niệm số đối. Lời giải chi tiết :
Số đối của \(\frac{5}{6}\) là \( - \frac{5}{6}\).
Câu 3 :
Căn bậc hai số học của 196 là:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của 196 là \(\sqrt {196} = 14\).
Câu 4 :
Số nào là số vô tỉ trong các số sau:
Đáp án : C Phương pháp giải :
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn. Lời giải chi tiết :
Ta có: \(\sqrt {\frac{1}{9}} = \frac{1}{3};0 = \frac{0}{1}\). Các số \(\frac{5}{{11}};\sqrt {\frac{1}{9}} ;0\) là số hữu tỉ nên không phải là số vô tỉ. Vậy chỉ có \(\sqrt {12} \) là số vô tỉ.
Câu 5 :
Cho \(\widehat {{\rm{xOy}}} = {70^0}\)và tia Ot là tia phân giác của \(\widehat {{\rm{xOy}}}\). Số đo \(\widehat {{\rm{xOt}}}\) bằng:
Đáp án : A Phương pháp giải :
Dựa vào kiến thức về tia phân giác. Lời giải chi tiết :
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.70^0} = {35^0}\).
Câu 6 :
Cho hình vẽ bên, biết \({\widehat {\rm{O}}_1} = {60^0}\). Số đo \({\widehat {\rm{O}}_3}\) là:
Đáp án : C Phương pháp giải :
Góc \({O_1}\) và góc \({O_3}\) là hai góc đối đỉnh nên \(\widehat {{O_1}} = \widehat {{O_3}}\). Lời giải chi tiết :
Vì góc \({O_1}\) và góc \({O_3}\) là hai góc đối đỉnh nên \(\widehat {{O_1}} = \widehat {{O_3}}\). Mà \(\widehat {{O_1}} = {60^0}\) nên \(\widehat {{O_3}} = {60^0}\).
Câu 7 :
Đường trung trực của một đoạn thẳng là
Đáp án : D Phương pháp giải :
Dựa vào khái niệm đường trung trực của một đoạn thẳng. Lời giải chi tiết :
Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng ấy tại trung điểm của nó
Câu 8 :
Cho hai tam giác \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat B = \widehat P\), \(BC = PN\). Cần thêm điều kiện nào để \(\Delta ABC = \Delta MPN\) theo trường hợp góc – cạnh – góc
Đáp án : B Phương pháp giải :
Dựa vào trường hợp bằng nhau góc – cạnh – góc. Lời giải chi tiết :
Để \(\Delta ABC = \Delta MPN\) theo trường hợp góc – cạnh – góc mà đã có \(\widehat B = \widehat P\), \(BC = PN\) thì \(\widehat C = \widehat N\).
Câu 9 :
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu định lượng?
Đáp án : B Phương pháp giải :
Dựa vào phân loại dữ liệu: Dữ liệu được chia thành hai loại: dữ liệu định tính và dữ liệu định lượng. Lời giải chi tiết :
Trong các dữ liệu trên, chỉ có dữ liệu quốc tích của các học sinh trong trường quốc tế không phải là dữ liệu định lượng.
Câu 10 :
Cho hình vẽ sau có \(\widehat B = {48^O},\widehat {AED} = {65^O}\). Số đo \(\widehat {BAD}\) bằng
Đáp án : D Phương pháp giải :
Dựa vào tính chất tam giác cân, định lí tổng 3 góc trong một tam giác và tính chất của hai góc kề bù. Lời giải chi tiết :
Xét tam giác ADE có \(AD = AE\) nên tam giác ADE cân tại A suy ra \(\widehat {ADE} = \widehat {AED} = {65^0}\). Vì góc ADB và góc ADE là hai góc kề bù nên \(\widehat {ADB} + \widehat {ADE} = {180^0}\) suy ra \(\widehat {ADB} = {180^0} - {65^0} = {115^0}\). Xét tam giác ABD, ta có: \(\widehat {BAD} + \widehat {ADB} + \widehat B = {180^0}\) (tổng 3 góc trong một tam giác). \( \Rightarrow \widehat {BAD} = {180^0} - \widehat B - \widehat {ADB} = {180^0} - {48^0} - {115^0} = {17^0}\).
Câu 11 :
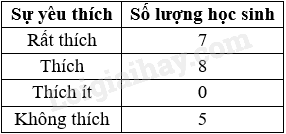
Kết quả tìm hiểu về sở thích chơi game của một số học sinh trong một trường THCS được ghi bởi bảng thống kê sau. Hãy cho biết nhiều học sinh lựa chọn loại nào nhất?
Đáp án : A Phương pháp giải :
Quan sát bảng thống kê, lập bảng số liệu biểu thị sở thích chơi game của các học sinh đó theo số lượng để biết học sinh lựa chọn loại nào nhiều nhất. Lời giải chi tiết :
Ta có bảng số liệu sở thích chơi game của các học sinh theo số lượng như sau:
Quan sát bảng số liệu trên, ta thấy học sinh lựa chọn “Thích” có số lượng nhiều nhất.
Câu 12 :
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) xếp loại học lực giữa kì I của học sinh lớp 7A. Hỏi học sinh đạt loại gì là nhiều nhất?
Đáp án : B Phương pháp giải :
Quan sát biểu đồ để xác định. Lời giải chi tiết :
Quan sát biểu đồ trên, ta thấy số học sinh khá chiếm tỉ lệ nhiều nhất (40%).
II. Tự luận
Phương pháp giải :
Sử dụng các quy tắc thực hiện phép tính. Lời giải chi tiết :
a) \({\left( {\frac{2}{3} - 1} \right)^2} - \frac{3}{5}:\frac{9}{{10}} + {1^{2022}}\) \(\begin{array}{l} = {\left( {\frac{2}{3} - \frac{3}{3}} \right)^2} - \frac{3}{5} \cdot \frac{{10}}{9} + 1\\ = {\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{2}{3} + 1\\{\rm{ = }}\frac{1}{9} - \frac{6}{9} + \frac{9}{9}\\ = \frac{4}{9}\end{array}\) b) \(\frac{8}{7} \cdot \left| {\frac{{ - 3}}{5}} \right| + \frac{8}{7} \cdot \sqrt {\frac{4}{{25}}} - \frac{{\sqrt 9 }}{4}\) \(\begin{array}{l} = \frac{8}{7} \cdot \frac{3}{5} + \frac{8}{7} \cdot \frac{2}{5} - \frac{3}{4}\\ = \frac{8}{7} \cdot \left( {\frac{3}{5} + \frac{2}{5}} \right) - \frac{3}{4} = \frac{8}{7} \cdot 1 - \frac{3}{4}\\ = \frac{{32}}{{28}} - \frac{{21}}{{28}} = \frac{{11}}{{28}}\end{array}\) Phương pháp giải :
a) Dựa vào quy tắc chuyển vế để tìm x. b) Chia hai trường hợp: \(\frac{1}{2} - x = \frac{4}{5}\) hoặc \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\). Lời giải chi tiết :
a) \(x + 0,75 = \frac{2}{3}\) \(\begin{array}{l}x + \frac{3}{4} = \frac{2}{3}\\x = \frac{2}{3} - \frac{3}{4}\\x = \frac{{ - 1}}{{12}}\end{array}\) Vậy \(x = \frac{{ - 1}}{{12}}\). b) \(\left| {\frac{1}{2} - x} \right| = \frac{4}{5}\) thì \(\frac{1}{2} - x = \frac{4}{5}\) hoặc \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\). TH1. \(\frac{1}{2} - x = \frac{4}{5}\) \(\begin{array}{l}x = \frac{1}{2} - \frac{4}{5}\\x = \frac{{ - 3}}{{10}}\end{array}\) TH2. \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\) \(\begin{array}{l}x = \frac{1}{2} + \frac{4}{5}\\x = \frac{{13}}{{10}}\end{array}\) Vậy \(x \in \left\{ {\frac{{ - 3}}{{10}};\frac{{13}}{{10}}} \right\}\). Phương pháp giải :
Dựa vào cách làm tròn số với độ chính xác cho trước. Lời giải chi tiết :
Ta có: 331 698 \( \approx \) 332 000. Vậy diện tích nước Việt Nam được làm tròn đến hàng nghìn là khoảng 332 000 km2. Phương pháp giải :
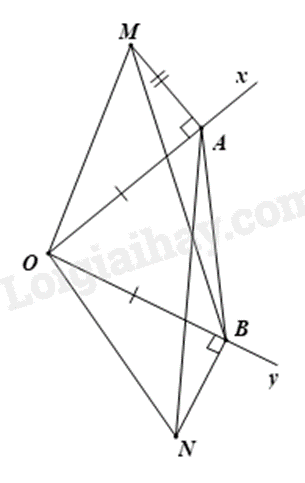
a. \(\Delta OMA = \Delta ONB\left( {c - g - c} \right)\) b. Theo a suy ra \(\widehat {AOM}\)=\(\widehat {BON}\) Suy ra \(\widehat {AOM}\)+\(\widehat {AOB}\)=\(\widehat {AOB}\)+\(\widehat {BON}\) Suy ra \(\widehat {AON\,}\)=\(\widehat {BOM}\) Chứng minh \(\Delta OMB = \Delta ONA\left( {c - g - c} \right)\) Suy ra \(\widehat {OMB}\)=\(\widehat {ONA}\) Lời giải chi tiết :
a. \(\Delta OMA = \Delta ONB\left( {c - g - c} \right)\) b. Theo a suy ra \(\widehat {AOM}\)=\(\widehat {BON}\) Suy ra \(\widehat {AOM}\)+\(\widehat {AOB}\)=\(\widehat {AOB}\)+\(\widehat {BON}\) Suy ra \(\widehat {AON\,}\)=\(\widehat {BOM}\) Chứng minh \(\Delta OMB = \Delta ONA\left( {c - g - c} \right)\) Suy ra \(\widehat {OMB}\)=\(\widehat {ONA}\) Phương pháp giải :
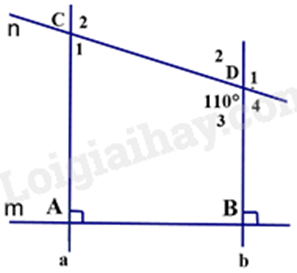
a) Chứng minh a và b cùng vuông góc với m nên song song với nhau. b) Dựa vào kiến thức về hai góc đối, hai đường thẳng song song để tính số đo \({\widehat {\rm{D}}_1}\) và \(\widehat {{\rm{ ACD}}}\). Lời giải chi tiết :
a) Vì \(m \bot a;m \bot b\) (gt) nên a // b (đpcm). b) Ta có: \(\widehat {{D_1}} = \widehat {{D_3}} = {110^0}\) (hai góc đối đỉnh). Ta có: a // b (cmt) suy ra:\({\rm{ }}{\widehat {\rm{C}}_2} = {\widehat {\rm{D}}_3} = {110^0}\)(2 góc so le trong) Ta có:\({\rm{ }}{\widehat {\rm{C}}_2} + {\widehat {\rm{C}}_1} = {180^0}\) (2 góc kề bù) \(\begin{array}{l}{110^0} + {\widehat {\rm{C}}_1} = {180^0}\\{\widehat {\rm{C}}_1} = {180^0} - {110^0} = {70^0}\end{array}\) Vậy \(\widehat {{D_1}} = {110^0};\widehat {{C_1}} = {70^0}\).
|














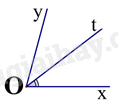










Danh sách bình luận