Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các số sau, số nào không phải là số hữu tỉ?
Câu 2 :
Khẳng định nào dưới đây sai?
Câu 3 :
Khẳng định nào dưới đây sai?
Câu 6 :
Đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B như hình vẽ. Khi đó kết luận nào sau đây là không đúng.
Câu 7 :
Giá trị của biểu thức \(P = \sqrt {100 - 36} + \sqrt {81} \) là:
Câu 9 :
Kết quả \({\left( { - \frac{2}{5}} \right)^3}\) là
Câu 10 :
Cho \(\widehat {xOy} = 80^\circ \), \(Ot\) là tia phân giác của \(\widehat {xOy}\). Số đo \(\widehat {xOt}\) bằng?
Câu 11 :
So sánh hai số hữu tỉ \( - 0,2\) và \(\frac{{ - 2}}{5}\)
Câu 12 :
Kết quả của phép tính \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2}\) là
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Trong các số sau, số nào không phải là số hữu tỉ?
Đáp án : B Phương pháp giải :
Số hữu tỉ là các số viết được dưới dạng \(\frac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) Lời giải chi tiết :
Số \(\sqrt {15} \) không phải là số hữu tỉ. Đáp án B.
Câu 2 :
Khẳng định nào dưới đây sai?
Đáp án : C Phương pháp giải :
Số đối của số hữu tỉ a là – a. Lời giải chi tiết :
Ta có: \( - \left( { - 5} \right) = 5\). Mà số đối của 5 là -5 nên đáp án C sai. Đáp án C.
Câu 3 :
Khẳng định nào dưới đây sai?
Đáp án : C Phương pháp giải :
Dựa vào khái niệm căn bậc hai số học: Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho \({x^2} = a\). Lời giải chi tiết :
Căn bậc hai số học của một số a là \(\sqrt a \) nên: + Căn bậc hai số học của 25 là \(\sqrt {25} = 5\). + Căn bậc hai số học của 0 là 0. + Căn bậc hai số học của 16 là \(\sqrt {16} = 4\) nên C sai. + Căn bậc hai số học của 3 là \(\sqrt 3 \). Đáp án C.
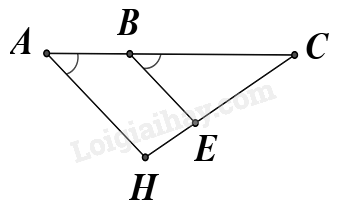
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Lời giải chi tiết :
Cặp góc \(\widehat {BAH}\) và \(\widehat {CBE}\) là một cặp góc đồng vị. Đáp án D.
Đáp án : D Phương pháp giải :
Chỉ có một đường thẳng song song với đường thẳng đó. Lời giải chi tiết :
Tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó. Đáp án D.
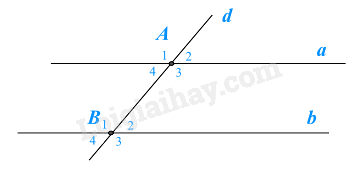
Câu 6 :
Đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B như hình vẽ. Khi đó kết luận nào sau đây là không đúng.
Đáp án : A Phương pháp giải :
Sử dụng tính chất của hai đường thẳng song song, tính chất hai góc kề bù. Lời giải chi tiết :
Vì đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc đồng vị) nên B đúng. Khi đó \(\widehat {{A_1}} + \widehat {{B_4}} = \widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \) (vì \(\widehat {{B_1}}\) và \(\widehat {{B_4}}\) là hai góc kề bù) nên D đúng. \(\widehat {{A_1}} = \widehat {{A_3}}\) vì là hai góc đối đỉnh nên C đúng. Do đó đáp án A sai. Đáp án A.
Câu 7 :
Giá trị của biểu thức \(P = \sqrt {100 - 36} + \sqrt {81} \) là:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức căn bậc hai của một số. Lời giải chi tiết :
\(P = \sqrt {100 - 36} + \sqrt {81} = \sqrt {64} + \sqrt {81} = 8 + 9 = 17\). Đáp án C.
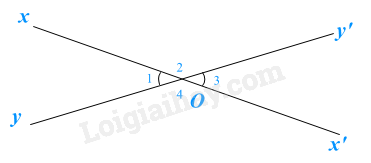
Đáp án : D Phương pháp giải :
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Lời giải chi tiết :
Trong hình trên có hai cặp góc đối đỉnh là \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\); \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). Đáp án D.
Câu 9 :
Kết quả \({\left( { - \frac{2}{5}} \right)^3}\) là
Đáp án : C Phương pháp giải :
Sử dụng \({\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}\). Lời giải chi tiết :
\({\left( { - \frac{2}{5}} \right)^3} = - {\left( {\frac{2}{5}} \right)^3} = \frac{{{2^3}}}{{{5^3}}} = - \frac{8}{{125}}\). Đáp án C.
Câu 10 :
Cho \(\widehat {xOy} = 80^\circ \), \(Ot\) là tia phân giác của \(\widehat {xOy}\). Số đo \(\widehat {xOt}\) bằng?
Đáp án : D Phương pháp giải :
Sử dụng tính chất tia phân giác của một góc. Lời giải chi tiết :
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.80^\circ = 40^\circ \) Đáp án D.
Câu 11 :
So sánh hai số hữu tỉ \( - 0,2\) và \(\frac{{ - 2}}{5}\)
Đáp án : C Phương pháp giải :
Đưa hai số về phân số và thực hiện so sánh. Lời giải chi tiết :
Ta có: \( - 0,2 = \frac{{ - 2}}{{10}} = \frac{{ - 1}}{5}\). Vì \(\frac{{ - 1}}{5} > \frac{{ - 2}}{5}\) nên \( - 0,2 > \frac{{ - 2}}{5}\). Đáp án C.
Câu 12 :
Kết quả của phép tính \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2}\) là
Đáp án : C Phương pháp giải :
Thực hiện lần lượt phép tính. Lời giải chi tiết :
Ta có: \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2} = \left( {\frac{{11}}{{12}}.\frac{{16}}{{33}}} \right).\frac{3}{2} = \frac{4}{9}.\frac{3}{2} = \frac{2}{3}\). Đáp án C.
II. Tự luận
Phương pháp giải :
a), b) Sử dụng quy tắc tính với số hữu tỉ. c) Sử dụng quy tắc nhân, chia lũy thừa cùng cơ số. Lời giải chi tiết :
a) \(0,2 + \frac{3}{5}:\frac{{ - 3}}{2}\) \(\begin{array}{l} = \frac{1}{5} + \frac{3}{5}.\frac{{ - 2}}{3}\\ = \frac{1}{5} + \frac{{ - 2}}{5}\\ = \frac{{ - 1}}{5}\end{array}\) b) \(\frac{4}{5}.\frac{3}{{13}} + 0,8.\frac{{10}}{{13}} - \frac{7}{5}\) \(\begin{array}{l} = \frac{4}{5}.\frac{3}{{13}} + \frac{4}{5}.\frac{{10}}{{13}} - \frac{7}{5}\\ = \frac{4}{5}\left( {\frac{3}{{13}} + \frac{{10}}{{13}}} \right) - \frac{7}{5}\\ = \frac{4}{5} - \frac{7}{5}\\ = \frac{{ - 3}}{5}\end{array}\) c) \(\frac{{{3^8}{{.3}^{18}}}}{{{{27}^5}{{.9}^6}}}\)\( = \frac{{{3^8}{{.3}^{18}}}}{{{{\left( {{3^3}} \right)}^5}{{.3}^{12}}}} = \frac{{{3^{26}}}}{{{3^{27}}}} = \frac{1}{3}\) Phương pháp giải :
a), b) Sử dụng quy tắc tính với số hữu tỉ. c) Sử dụng quy tắc nhân, chia lũy thừa cùng cơ số. Lời giải chi tiết :
a) $\frac{4}{5}-x=\frac{3}{4}$ $ x=\frac{4}{5}-\frac{3}{4} $ $x=\frac{1}{20} $ Vậy $x=\frac{1}{20}$. b) $\frac{5}{6}+\frac{1}{10}:x=\frac{4}{5}$ $ \frac{1}{10}:x=\frac{4}{5}-\frac{5}{6} $ $\frac{1}{10}:x=\frac{-1}{30}$ $ x=\frac{1}{10}:\frac{-1}{30} $ $ x=-3 $ Vậy $x=-3$ c) ${{\left( \frac{3}{5}-x \right)}^{2}}=\frac{9}{25}$ ${{\left( \frac{3}{5}-x \right)}^{2}}={{\left( \frac{3}{5} \right)}^{2}}$ TH1: $\frac{3}{5}-x=\frac{3}{5}$ $ x=\frac{3}{5}-\frac{3}{5} $ $x=0 $ TH2: $\frac{3}{5}-x=-\frac{3}{5}$ $ x=\frac{3}{5}-\left( -\frac{3}{5} \right) $ $ x=\frac{6}{5} $ Vậy $x=0$; $x=\frac{6}{5}$. Phương pháp giải :
Tính khối lượng gạo cửa hàng bán trong ngày thứ nhất, ngày thứ hai, ngày thứ ba. Từ đó tính tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất. Lời giải chi tiết :
Khối lượng gạo cửa hàng bán trong ngày thứ nhất là: \(\frac{3}{8}.160 = 60\left( {kg} \right)\) Khối lượng gạo cửa hàng bán trong ngày thứ hai là: \(\frac{1}{4}\left( {160 - 60} \right) = 25\left( {kg} \right)\) Khối lượng gạo cửa hàng bán trong ngày thứ ba là: \(160 - 60 - 25 = 75\left( {kg} \right)\) Tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất là: \(\frac{{75}}{{60}} = \frac{5}{4}\). Vậy tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất là \(\frac{5}{4}\). Phương pháp giải :
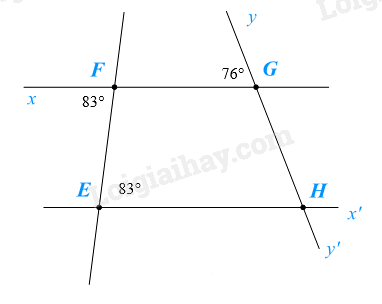
a) Dựa vào dấu hiệu nhận biết hai đường thẳng song song. b) Dựa vào tính chất của hai đường thẳng song song, hai góc đối đỉnh. Lời giải chi tiết :
a) Ta có: \(\widehat {xFE} = 83^\circ \), \(\widehat {FEH} = 83^\circ \) nên \(\widehat {xFE} = \widehat {FEH}\). Mà hai góc này là hai góc so le trong nên \(FG//EH\). b) Ta có: \(FG//EH\) nên \(\widehat {FGy} = \widehat {EHG}\) (hai góc đồng vị) Suy ra \(\widehat {EHG} = 76^\circ \). Ta có: \(\widehat {x'Hy'} = \widehat {EHG} = 76^\circ \) (hai góc đối đỉnh) Vậy \(\widehat {x'Hy'} = 76^\circ \). Phương pháp giải :
Nhân cả hai vế của A với 3. Tính 2A. Suy ra giá trị của A, so sánh với \(\frac{1}{2}\). Lời giải chi tiết :
Ta có: \(3A = 3.\left( {\frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}}} \right) = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2021}}}} + \frac{1}{{{3^{2022}}}}\) Suy ra \(\begin{array}{l}3A - A = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2021}}}} + \frac{1}{{{3^{2022}}}} - \left( {\frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}}} \right)\\2A = 1 - \frac{1}{{{3^{2023}}}}\end{array}\) Do đó \(A = \frac{1}{2}\left( {1 - \frac{1}{{{3^{2023}}}}} \right)\). Mà \(1 - \frac{1}{{{3^{2023}}}} < 1\) nên \(A = \frac{1}{2}\left( {1 - \frac{1}{{{3^{2023}}}}} \right) < \frac{1}{2}.1 = \frac{1}{2}\) hay \(A < \frac{1}{2}\).
|
























Danh sách bình luận