Đề thi học kì 2 Toán 7 - Đề số 9

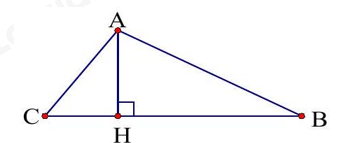
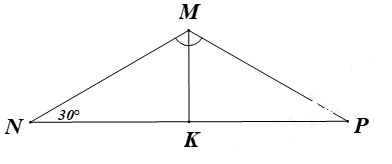
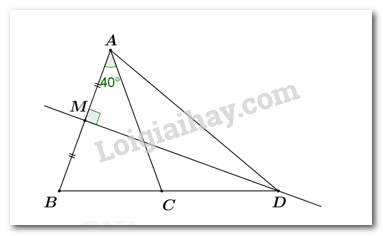
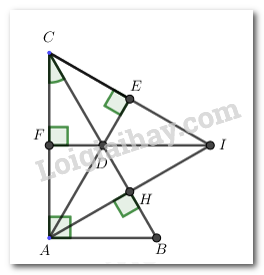
Đề bài

I. TRẮC NGHIỆM (2 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Đa thức \(M = 2{x^5} + {x^4} + 1 - {x^3} + 3{x^2} - 2{x^5} - {x^4}\) có bậc là

     A. 3.                                   B. 2.                                   C. 4.                                   D. 5.

Câu 2: Cho hình vẽ bên. Biết rằng \({\rm{AB}} > {\rm{AC}},{\rm{AH}} \bot {\rm{BC}}\). Kết luận nào sau đây đúng?

     A. \({\rm{HB}} > {\rm{AB}}\).                                         B. \({\rm{AC}} < {\rm{HC}}\).           C. \({\rm{HB}} < {\rm{HC}}\).                             D. \({\rm{HB}} > {\rm{HC}}\).

Câu 3: Cho \(\Delta MNP\) có MK là tia phân giác góc M, \(\hat N = \hat P = 30^\circ \). Khi đó số đo của \(\widehat {MKN}\) là:

     A. \({30^\circ }\).              B. \({60^\circ }\).              C. \({90^\circ }\).              D. \({120^\circ }\).

Câu 4: Trong tam giác \({\rm{ABC}}\). Kết luận nào sau đây đúng ?

     A. \({\rm{BC}} + {\rm{AC}} < {\rm{AB}}\).                        B. \({\rm{BC}} - {\rm{AC}} > {\rm{AB}}\).     C. \({\rm{BC}} + {\rm{AC}} > {\rm{AB}}\).                        D. \({\rm{BC}} - {\rm{AC}} = {\rm{AB}}\).

Câu 5: Đa thức \({\rm{g}}\left( {\rm{x}} \right) = {{\rm{x}}^2} + x - 2\) có một nghiệm là

     A. \(x = 2\).                         B. \(x = 0\).                         C. \(x = 3\).                         D. \(x = 1\).

Câu 6: Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là B = {1; 2; 3; … ; 29;30}. Tính xác suất để kết quả rút ra là một thẻ có số chia hết cho 3

     A. 6                                    B. 30                                  C. \(\dfrac{1}{2}\)               D. \(\dfrac{1}{3}\)

Câu 7: Cho \(P(x) = {x^2} - 6x + a\) . Tìm \(a\)  để \(P\left( x \right)\) nhận \( - 1\)  là nghiệm.

     A. \(a = 1\)                          B. \(a = {\rm{\;}} - 7\)                                                     C. \(a = 7\)                      D. \(a = 6\)

Câu 8: Cho tam giác ABC cân tại A có \(\angle A = {40^0}\), đường trung trực của AB cắt BC tại D. Tính \(\angle CAD\).

     A. 30⁰.                               B. 45⁰.                               C. 60⁰.                               D. 40⁰.

PHẦN 2. TỰ LUẬN (8 điểm)

Câu 1: (2 điểm) Cho hai đa thức \({\rm{A}}\left( {\rm{x}} \right) = 2{{\rm{x}}^2} - {\rm{x}} + 3\) và \({\rm{B}}\left( {\rm{x}} \right) = {x^4}{\rm{ \; +  \;2}}{{\rm{x}}^2} + {\rm{x}} - 1\).

a) Tính giá trị của A(x) và B(x) tại  \(x = 2; x = {\rm{ \;}} - 1\).

b) Tính N(x); M(x) biết              \({\rm{N}}\left( {\rm{x}} \right) = {\rm{A}}\left( {\rm{x}} \right) + {\rm{B}}\left( {\rm{x}} \right)\); \(A\left( x \right) + M\left( x \right) = B\left( x \right)\).

c) Chứng tỏ đa thức \(N\left( x \right)\) không có nghiệm.

Câu 2: Chia đa thức A cho B sau đó xác định thương và dư trong phép chia.

a) \(A = 2{x^4} - 4{x^3} + 6{x^2} + 3x;\)\(B = 2x\)

b) \(A = 2{x^4} - 3{x^3} - 3{x^2} + 6x - 2\);\(B = {x^2} - 2\)

Câu 3: (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao AH. Trên đoạn HC lấy điểm \(D\) sao cho \(HD = HB.\)

a) Chứng minh \(\Delta AHB = \Delta AHD\).

b) Chứng minh \(\Delta ABD\) là tam giác đều.

c) Từ \(C\) kẻ CE vuông góc với đường thẳng AD\(\left( {E \in AD} \right)\). Chứng minh \(DE = HB\).

d) Từ \(D\) kẻ DF vuông góc với AC\((\)F thuộc AC\(),\) I là giao điểm của CE và AH. Chứng minh ba điểm \(I, D, F\) thẳng hàng.

Câu 4: (0,5 điểm) Cho các số thực \(a,b,c,x,y,z \ne 0\) thoả mãn \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\).

Chứng minh rằng: \(\dfrac{{{x^2} + {y^2} + {z^2}}}{{{{\left( {ax + by + cz} \right)}^2}}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}}\).

Lời giải

I. Trắc nghiệm

Câu 1.

Phương pháp:

Rút gọn rồi xác định bậc của đa thức.

Cách giải:

\(M = {x^5} + {x^4} + 1 - {x^3} + 3{x^2} - {x^5} - {x^4} = {\rm{ \;}} - {x^3} + 3{x^2} + 1\).

Bậc của đa thức là 3.

Chọn A.

Câu 2.

Phương pháp:

Đoạn thẳng nào lớn hơn thì hình chiếu sẽ lớn hơn.

Cách giải:

Vì AB > AC \( \Rightarrow \) HB > CH

Chọn D.

Câu 3.

Phương pháp:

Tính chất tổng 3 góc của một tam giác và tính chất tia phân giác của góc.

Cách giải:

Ta có: \(\widehat {NMP} = {180^\circ }{\rm{ \;}} - \hat N - \hat P = {180^\circ }{\rm{ \;}} - {30^\circ }{\rm{ \;}} - {30^\circ }{\rm{ \;}} = {120^\circ }\)

Vì MK là phân giác của góc NMP nên \(\widehat {NMK} = \dfrac{{\widehat {NMP}}}{2} = \dfrac{{{{120}^\circ }}}{2} = {60^\circ }\)\( \Rightarrow \widehat {MKN} = {180^\circ }{\rm{ \;}} - {30^\circ }{\rm{ \;}} - {60^\circ }{\rm{ \;}} = {90^\circ }\).  

Chọn C.

Câu 4

Phương pháp:

Đựa vào bất đẳng thức tam giác, tổng 2 cạnh của một tam giác luôn lớn hơn cạnh thứ ba.

Cách giải:

Đáp án đúng \({\rm{BC}} + {\rm{AC}} > {\rm{AB}}\).

Chọn C.

Câu 5.

Phương pháp:

Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì ta nói a (hoặc x = a ) là một nghiệm của đa thức đó.

Cách giải:

Thay các giá trị của x vào đa thức ta có:

\({\rm{g}}\left( 2 \right) = {2^2} + 2 - 2 = 4\)

\({\rm{g}}\left( 0 \right) = {0^2} + 0 - 2 = {\rm{ \;}} - 2\)

\({\rm{g}}\left( 3 \right) = {3^2} + 3 - 2 = 7\)

\({\rm{g}}\left( 1 \right) = {1^2} + 1 - 2 = 0\)

Vậy \(x = 1\) là nghiệm của đa thức.

Chọn D.

Câu 6

Phương pháp:

Tìm các số chia hết cho 3 từ 0 đến 30.

Cách giải:

Các số chia hết cho 3 từ tập B = {1; 2; 3; … ; 29; 30} là 3,6,9,12,15,18,21,24,27,30

=> có tất cả 10 số chia hết cho 3

Vậy xác suất để thẻ rút ra là số chia hết cho 3 là \(\dfrac{{10}}{{30}} = \dfrac{1}{3}\).

Chọn D.

Câu 7

Phương pháp:

\(P\left( x \right)\) nhận \( - 1\)  là nghiệm nên \(P\left( { - 1} \right) = 0,\) từ đó ta tìm được a.

Cách giải:

\(P\left( x \right)\) nhận \( - 1\)  là nghiệm nên \(P\left( { - 1} \right) = 0,\)

\( \Rightarrow {( - 1)^2} - 6.( - 1) + a = 0 \Rightarrow 1 + 6 + a = 0\)

\( \Rightarrow 7 + a = 0   \Rightarrow a = {\rm{\;}} - 7\)

 Vậy \(P\left( x \right)\) nhận \( - 1\)  là nghiệm thì \(a = {\rm{\;}} - 7\).

Chọn B.

Câu 8.

Phương pháp:

Sử dụng tính chất đường trung trực của đoạn thẳng: Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Chứng minh hai tam giác bằng nhau.

Cộng, trừ góc.

Cách giải:

Gọi M là trung điểm của AB.

Vì D thuộc trung trực của đoạn thẳng AB nên DA = DB (tính chất đường trung trực của đoạn thẳng).

Xét \(\Delta AMD\) và \(\Delta BMD\) có:

MA = MB (do M là trung điểm của AB).

MD chung

DA = DB (cmt)

\( \Rightarrow \Delta AMD = \Delta BMD \left( {c.c.c} \right)\)

\( \Rightarrow \angle MAD = \angle MBD\) (hai góc tương ứng).

Tam giác ABC cân tại A nên \(\angle MBD = \angle ACB = \dfrac{{{{180}^0} - \angle BAC}}{2} = \dfrac{{{{180}^0} - {{40}^0}}}{2} = {70^0}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \angle MAD = {{70}^0}}\\{ \Rightarrow \angle MAC + \angle CAD = {{70}^0}}\\{ \Rightarrow {{40}^0} + \angle CAD = {{70}^0}}\\{ \Rightarrow \angle CAD = {{30}^0}}\end{array}\)

Chọn A.

II. Tự luận

Bài 1:

Phương pháp:

a) Thay lần lượt \(x = 2; x = {\rm{ \;}} - 1\) vào đa thức để tính giá trị;

b) Sử dụng các quy tắc cộng, trừ đa thức;

c) Chứng minh không có giá trị của x đê đa thức nhận giá trị bằng 0.

Cách giải:

a) \({\rm{A}}\left( 2 \right) = 2.{\left( 2 \right)^2} - 2 + 3 = 8 - 2 + 3 = 9\);\({\rm{A}}\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} - \left( { - 1} \right) + 3 = 6\)

\({\rm{B}}\left( 2 \right) = {2^4}{\rm{ \; +  \;2}}.{{\rm{2}}^2} + 2 - 1 = 32 + 8 + 2 - 1 = 41\);\({\rm{B}}\left( { - 1} \right) = {\left( { - 1} \right)^4}{\rm{ \; +  \;2}}.{\left( { - 1} \right)^2} + \left( { - 1} \right) - 1 = 1 + 2 - 1 - 1 = 1\).

b\({\rm{N}}\left( {\rm{x}} \right) = {\rm{A}}\left( {\rm{x}} \right) + {\rm{B}}\left( {\rm{x}} \right) = 2{{\rm{x}}^2} - {\rm{x}} + 3 + {x^4}{\rm{ \; +  \;2}}{{\rm{x}}^2} + {\rm{x}} - 1 = {x^4} + \left( {2{x^2} + 2{x^2}} \right) + \left( {x - x} \right) + \left( {3 - 1} \right) = {x^4} + 4{x^2} + 2\).

\(A\left( x \right) + M\left( x \right) = B\left( x \right) \Rightarrow M\left( x \right) = B\left( x \right) - A\left( x \right) = {x^4}{\rm{ \; +  \;2}}{{\rm{x}}^2} + {\rm{x}} - 1 - \left( {2{{\rm{x}}^2} - {\rm{x}} + 3} \right)\).

\(\begin{array}{*{20}{l}}{M\left( x \right) = {x^4}{\rm{ \; +  \;2}}{{\rm{x}}^2} + {\rm{x}} - 1 - 2{{\rm{x}}^2}{\rm{ +  \;x \; -  \;3}}}\\{M\left( x \right) = {x^4} + 2x - 4}\end{array}\)

Vậy \(N\left( x \right) = {x^4} + 4{x^2} + 2\);\(M\left( x \right) = {x^4} + 2x - 4\).

c) Ta có \(N\left( x \right) = {x^4} + 4{x^2} + 2\) mà \({x^4} + 4{x^2} \ge 0 \Rightarrow {x^4} + 4{x^2} + 2 > 0\) với mọi x.

Vậy N(x) không có nghiệm.

Câu 2:

Phương pháp:

Sử dụng cách chia đa thức cho đa thức.

Cách giải:

a) \(A:B = \left( {2{x^4} - 4{x^3} + 6{x^2} + 3x} \right):2x = {x^3} - 2{x^2} + 3x + \dfrac{3}{2}\)

Thương của phép chia là \({x^3} - 2{x^2} + 3x + \dfrac{3}{2}\) dư 0.

b)

Thương của phép chia là \(2{x^2} - 3x + 1\) dư 0.

Câu 3:

Phương pháp:

a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.

b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.

c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).

d) Chứng minh \(FD//AB\) rồi sau đó chứng minh \(DI//AB\), suy ra \(I, D, F\) là ba điểm thẳng hàng.

Cách giải:

a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có:  

\(HD = HB\) (gt)

\(AH chung\)

\(\angle AHB = \angle AHD = {90^0}\)

\( \Rightarrow \)\(\Delta AHB = \Delta AHD\) (c.g.c)

b) \(\Delta ABC\) vuông tại \(A\),

có \(\angle C = {30^0} \Rightarrow \angle B = {90^0} - {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác).

Vì \(\Delta AHB = \Delta AHD\) (cmt)

\( \Rightarrow AB = AD\) (hai cạnh tương ứng).

\( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\)

Do đó: \(\Delta ABD\)là tam giác đều.

c) Vì \(\Delta ABD\)là tam giác đều (cmt)

\( \Rightarrow \angle DAB = {60^0}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow \angle CAD = {{90}^0} - \angle DAB}\\{   = {{90}^0} - {{60}^0}}\\{   = {{30}^0}}\end{array}\)

Xét \(\Delta ACD\) có \(\angle ACD = \angle CAD = {30^0}\).

\( \Rightarrow \Delta ACD\) cân tại D.

\( \Rightarrow CD = AD\)

Xét \(\Delta DEC\) và \(\Delta DHA\) có:

\(CD = AD \left( {cmt} \right)\)

\(\angle E = \angle H = {90^0}\)

\(\angle CDE = \angle ADH\) (đối đỉnh)

\( \Rightarrow \Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn).

\( \Rightarrow DE = DH\) (hai cạnh tương ứng).

Mà \(DH = DB\) (giả thiết)

\( \Rightarrow DE = DB\).

d) Từ \(D\) kẻ DF vuông góc với AC\((\)F thuộc AC\(),\) I là giao điểm của CE và AH. Chứng minh ba điểm \(I, D, F\) thẳng hàng.

Ta có:

\(\begin{array}{*{20}{l}}{DF \bot AC \left( {gt} \right)}\\{AB \bot AC\left( {gt} \right)}\\{ \Rightarrow DF//AB \left( 1 \right)}\end{array}\)

Ta lại có:

\(\angle FDC = \angle HDI\) (đối đỉnh)

Mà \(\angle FDC = {90^0} - \angle C = {90^0} - {30^0} = {60^0}\)

\( \Rightarrow \angle FDC = \angle HDI = {60^0}\)

Mà \(\angle B = {60^0}\)

\( \Rightarrow \angle B = \angle DHI\)

Mà hai góc này ở vị trí so le trong

Do đó: \(DI//AB\)  (2)

Từ (1) và (2), suy ra: \(\angle I,D,B\) là ba điểm thẳng hàng.

Câu 4:

Phương pháp:

Đặt \(\dfrac{a}{b} = \dfrac{c}{d} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = kb}\\{c = kd}\end{array}} \right.\). Sau đó thay vào từng vế của đẳng thức cần chứng minh, ta được cùng một biểu thức, suy ra điều phải chứng minh.

Cách giải:

Đặt \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = ka}\\{y = kb}\\{z = kc}\end{array}} \right.\)

Thay \(x = ka;y = kb;z = kc\) vào đẳng thức, ta được:

\(VT = \dfrac{{{{\left( {ka} \right)}^2} + {{\left( {kb} \right)}^2} + {{\left( {kc} \right)}^2}}}{{{{\left( {a.ka + b.kb + c.kc} \right)}^2}}} = \dfrac{{{k^2}{a^2} + {k^2}{b^2} + {k^2}{c^2}}}{{{{\left( {k{a^2} + k{b^2} + k{c^2}} \right)}^2}}} = \dfrac{{{k^2}\left( {{a^2} + {b^2} + {c^2}} \right)}}{{{k^2}{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}} = VP\)

\( \Rightarrow \dfrac{{{x^2} + {y^2} + {c^2}}}{{{{\left( {ax + by + cz} \right)}^2}}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}}\) (đpcm)

.