Đề thi học kì 1 Toán 7 - Đề số 9 - Kết nối tri thứcTải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
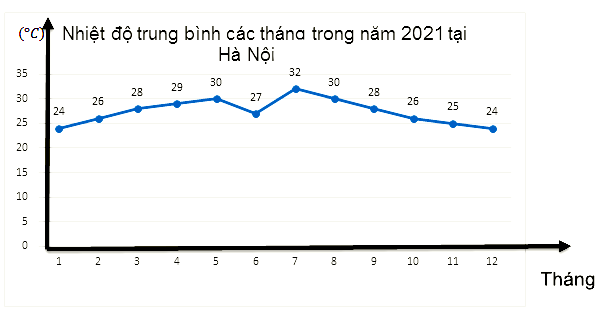
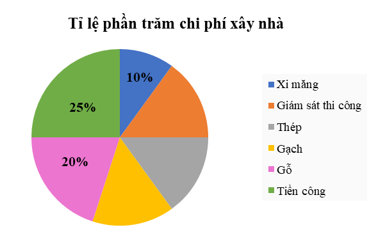
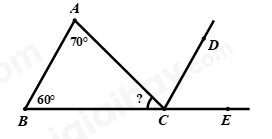
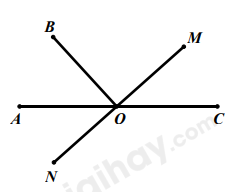
Đề bài Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1: Kết quả của phép tính: \(\left( {1 + 1\dfrac{1}{2}} \right):\dfrac{{ - 7}}{4}\) là: A. \(\dfrac{{20}}{{ - 7}}\) B. \(\dfrac{{10}}{{ - 7}}\) C. \(\dfrac{{ - 5}}{{ - 14}}\) D. \(\dfrac{5}{{ - 7}}\) Câu 2: Tìm \(x\), biết: \(x + \left( {\dfrac{1}{4}x - 2,5} \right) = \dfrac{{ - 11}}{{20}}\) A. \(x = \dfrac{{39}}{{25}}\) B. \(x = \dfrac{{19}}{{20}}\) C. \(x = \dfrac{{17}}{{20}}\) D. \(x = \dfrac{{11}}{{25}}\) Câu 3: Kết quả của biểu thức: \(2,8 + 3.\left| { - \dfrac{{13}}{3}} \right| + 0,2.\left| 6 \right| + 5.\left| {10} \right|\) là: A. \(41\) B. \(53\) C. \(47\) D. \(67\) Câu 4: Thứ tự tăng dần của các số: \(\sqrt {\dfrac{1}{{16}}} \,;\,4\dfrac{1}{7}\,;\,1,\left( 3 \right)\,;\,\sqrt {81} \,;\, - \sqrt {25} \,;\, - 12,1\) là: A. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 5\,\,;\,\, - 12,1\) B. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 12,1\,\,;\,\, - 5\) C. \( - 12,1\,\,;\,\, - 5\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \) D. \( - 5\,\,;\,\, - 12,1\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \) Câu 5: Cho biểu đồ sau: Tính nhiệt độ trung bình cả năm 2021. A. 27 B. 27,4 C. 28 D. 28,4 Câu 6: Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau: Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau. A. \(15\% \) B. \(12\% \) C. \(20\% \) D. \(45\% \) Câu 7: Cho hai góc kề bù \(AOB\) và \(BOC\). Tia \(OM\) nằm giữa hai tia \(OB\) và \(OC\). Tia \(ON\) là tia đối của tia \(OM\). Khi đó cặp góc đối đỉnh là cặp góc nào trong các góc sau đây? A. \(\angle BOM\) và \(\angle CON\) B. \(\angle AOB\) và \(\angle AON\) C. \(\angle AOM\) và \(\angle CON\) D. \(\angle COM\) và \(\angle CON\) Câu 8: Cho hình vẽ bên dưới. Biết \(AB//CD\)\(,\angle A = {70^0},\angle B = {60^0}.\) Tính số đo của góc \(ACB?\)
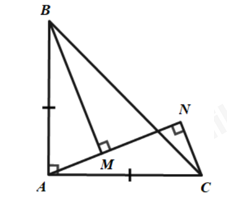
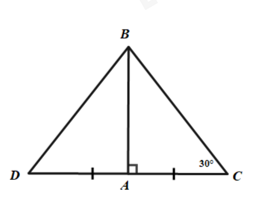
A. \(\angle ACB = {70^0}\) B. \(\angle ACB = {60^0}\) C. \(\angle ACB = {130^0}\) D. \(\angle ACB = {50^0}\) Câu 9: Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = AC\). Qua \(A\) kẻ đường thẳng \(d\) cắt \(BC\). Vẽ \(BM,CN\) vuông góc với \(d\) với \(M,N \in d\). Chọn đáp án sai: A. \(AM = CN\) B. \(BM = AN\) C. \(\angle ABM = \angle ACN\) D. \(\angle ABM = \angle CAN\) Câu 10: Tam giác \(ABC\) vuông tại \(A\) có \(\angle C = 30^\circ \). Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = AC\). Tính số đo \(\angle BDA\)? A. \(70^\circ \) B. \(30^\circ \) C. \(90^\circ \) D. \(60^\circ \)
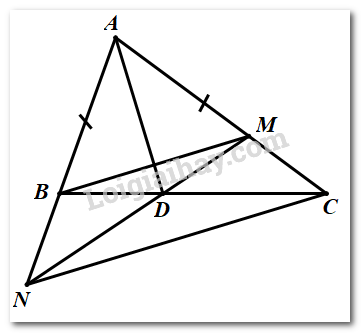
Phần II. Tự luận (7 điểm): Bài 1: (1,5 điểm) Thực hiện phép tính: a) \(\left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\) b) \(3.\sqrt {\dfrac{1}{9}} + 1,5.\sqrt {225} \) c) \(\left( { - 1,5} \right) + 2.\left| {2\dfrac{1}{2}} \right| - 6.\left| {\dfrac{{ - 16}}{3}} \right| + 5.\left| { - 0,3} \right|\) Bài 2: (1,5 điểm) Tìm \(x\), biết: a) \(x:\left( { - \dfrac{3}{5}} \right) = 1\dfrac{1}{4}\) b) \({\left( {0,9} \right)^9}:x = - {\left( {0,9} \right)^7}\) c) \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \) Bài 3: (3,5 điểm) Cho tam giác \(ABC\) có \(AB < AC\). Tia phân goác của các góc \(BAC\) cắt \(BC\) tại \(D\). Trên cạnh \(AC\) lấy điểm \(M\) sao cho \(AM = AB.\) a) Chứng minh \(\Delta ABD = \Delta AMD\) b) Chứng minh \(DB = DM\) và \(\angle ABD = \angle AMD\). c) Kéo dài \(AB\) và \(MD\) cắt nhau ở \(N\). Chứng minh \(\Delta BDN = \Delta MDC\). d) Chứng minh \(AD\) vuông góc với \(BM\) và \(BM\) song song với \(NC\). Bài 4: (0,5 điểm) Với a,b là số thực dương thoả mãn \(ab + a + b = 1\). Chứng minh rằng: \(\sqrt {2\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)} = 2\left( {a + b} \right)\) Lời giải Phần I: Trắc nghiệm:
Câu 1: Phương pháp: Đổi hỗn số về phân số Thực hiện phép cộng, phép chia số hữu tỉ. Cách giải: \(\left( {1 + 1\dfrac{1}{2}} \right):\dfrac{{ - 7}}{4} = \left( {1 + \dfrac{3}{2}} \right).\dfrac{4}{{ - 7}} = \left( {\dfrac{2}{2} + \dfrac{3}{2}} \right).\dfrac{4}{{ - 7}} = \dfrac{5}{2}.\dfrac{4}{{ - 7}} = \dfrac{{10}}{{ - 7}}\) Chọn B. Câu 2: Phương pháp: Vận dụng quy tắc chuyển vế tìm \(x\). Cách giải: \(x + \left( {\dfrac{1}{4}x - 2,5} \right) = \dfrac{{ - 11}}{{20}}\) \(\begin{array}{l}x + \dfrac{1}{4}x - \dfrac{{50}}{{20}} = \dfrac{{ - 11}}{{20}}\\\left( {1 + \dfrac{1}{4}} \right).x = \dfrac{{ - 11}}{{20}} + \dfrac{{50}}{{20}}\\\left( {\dfrac{4}{4} + \dfrac{1}{4}} \right).x = \dfrac{{39}}{{20}}\\\dfrac{5}{4}.x = \dfrac{{39}}{{20}}\\x = \dfrac{{39}}{{20}}:\dfrac{5}{4}\\x = \dfrac{{39}}{{20}}.\dfrac{4}{5}\\x = \dfrac{{39}}{{25}}\end{array}\) Vậy \(x = \dfrac{{39}}{{25}}\) Chọn A. Câu 3: Phương pháp: Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải: \(2,8 + 3.\left| { - \dfrac{{13}}{3}} \right| + 0,2.\left| 6 \right| + 5.\left| {10} \right|\) \(\begin{array}{l} = 2,8 + 3.\left[ { - \left( { - \dfrac{{13}}{3}} \right)} \right] + 0,2.6 + 5.10\\ = 2,8 + 3.\dfrac{{13}}{3} + 1,2 + 50\\ = 2,8 + 13 + 1,2 + 50\\ = 67\end{array}\) Chọn D. Câu 4: Phương pháp: Tính các căn bậc hai của một số, đổi từ số thập phân vô hạn tuần hoàn sang phân số. So sánh các phân số có cùng mẫu dương. Từ đó sắp xếp được các số theo thứ tự tăng dần. Cách giải: Ta có: \(\begin{array}{l}\sqrt {\dfrac{1}{{16}}} = \dfrac{1}{4} = \dfrac{{21}}{{84}};\\4\dfrac{1}{7} = \dfrac{{29}}{7} = \dfrac{{348}}{{84}};\\1,\left( 3 \right) = 1 + 3.0,1 = 1 + 3.\dfrac{1}{9} = 1 + \dfrac{1}{3} = \dfrac{3}{3} + \dfrac{1}{3} = \dfrac{4}{3} = \dfrac{{112}}{{84}};\\\sqrt {81} = 9 = \dfrac{{756}}{{84}};\\ - \sqrt {25} = - 5;\,\\ - 12,1.\end{array}\) Vì \(5 < 12,1\) nên \( - 5 > - 12,1\) Vì \(21 < 112 < 348 < 756\) nên \(\dfrac{{21}}{{84}} < \dfrac{{112}}{{84}} < \dfrac{{348}}{{84}} < \dfrac{{756}}{{84}}\) suy ra \(\sqrt {\dfrac{1}{{16}}} < 1,\left( 3 \right) < 4\dfrac{1}{7} < \sqrt {81} \) Thứ tự tăng dần của các số được sắp xếp là: \( - 12,1\,\,;\,\, - 5\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \). Chọn C. Câu 5: Phương pháp: Tính nhiệt độ trung bình cho 12 tháng từ tháng 1 đến tháng 12. Cách giải: Nhiệt độ trung bình năm 2021 là (24 + 26 + 28 + 29 + 30 + 27 + 32 + 30 + 28 + 26 + 25 + 24): 12 = 27,42 Chọn B. Câu 6: Phương pháp: Gọi tỉ lệ phần trăm chi phí gạch là \(x\% \) (điều kiện: \(x > 0\)) Từ hình quạt tròn biểu diễn 100%, từ đó tìm được \(x\) Cách giải: Gọi tỉ lệ phần trăm chi phí gạch là \(x\% \) (điều kiện: \(x > 0\)) Vì chi phí giám sát thi công, thép, gạch bằng nhau nên tỉ lệ phần trăm của chi phí giám sát thi công, thép là \(x\% \) Ta có: \(\begin{array}{l}x + x + x + 20\% + 25\% + 10\% = 100\% \\3x + 55\% = 100\% \\3x = 100\% - 55\% \\3x = 45\% \\x = 45\% :3\\x = 15\% \end{array}\) Vậy chi phí trả tiền gạch chiếm \(15\% \). Chọn A. Câu 7: Phương pháp: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Cách giải:
\(\angle AOB\) và \(\angle BOC\) là hai góc kề bù nên \(OA\) và \(OC\) là hai tia đối nhau Lại có: \(ON\) là tia đối của tia \(OM\) Do đó, \(\angle AOM\) và \(\angle CON\) là hai góc đối đỉnh. Chọn C. Câu 8: Phương pháp: Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc ở vị trí so le trong bằng nhau; hai góc ở vị trí đồng vị bằng nhau. Hai góc kề bù có tổng số đo góc bằng \({180^0}\). Cách giải: Vì \(AB//CD\) nên ta có: \(\angle BAC = \angle ACD = {70^0}\) (hai góc so le trong) \(\angle ABC = \angle DCE = {60^0}\) (hai góc đồng vị) Ta có: \(\angle ACD\) và \(\angle DCE\) là hai góc kề nhau nên \(\angle ACE = \angle ACD + \angle DCE = {70^0} + {60^0} = {130^0}\) Ta có: \(\angle ACB\) và \(\angle ACE\) là hai góc kề bù nên \(\angle ACB + \angle ACE = {180^0}\) \(\begin{array}{l} \Rightarrow \angle ACB + {130^0} = {180^0}\\ \Rightarrow \angle ACB = {180^0} - {130^0} = {50^0}\end{array}\) Vậy \(\angle ACB = {50^0}\) Chọn D. Câu 9: Phương pháp: Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau. Cách giải:
Vì \(\Delta ABC\) vuông tại \(A\) nên \(\angle BAC = \angle BAM + \angle CAM = 90^\circ \) \( \Rightarrow \angle BAM = 90^\circ - \angle CAM\) Và \(\Delta ANC\) vuông tại \(N\) nên \(\angle ACN + \angle CAM = 90^\circ \) (hai góc phụ nhau) \( \Rightarrow \angle ACN = 90^\circ - \angle CAM\) Do đó \(\angle BAM = \angle ACN\) Xét \(\Delta BAM\) và \(\Delta ACN\) có: \(\angle BMA = \angle ANC = 90^\circ \) \(\angle BAM = \angle ACN\) (cmt) \(AB = AC\) (gt) Nên \(\Delta BAM = \Delta ACN\) (cạnh huyền – góc nhọn). Suy ra: \(MA = NC\) (hai cạnh tương ứng) nên A đúng \(BM = AN\) (hai cạnh tương ứng) nên B đúng \(\angle ABM = \angle CAN\) (hai góc tương ứng) nên D đúng Chọn C. Câu 10: Phương pháp: + Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó. + Tam giác cân có 2 cạnh bên bằng nhau và 2 góc kề cạnh đáy bằng nhau. Cách giải: Vì \(AB \bot DC\) và \(AD = AC\) nên \(AB\) là đường trung trực của \(DC\) \( \Rightarrow BD = BC\) Suy ra \(\Delta DBC\) cân tại \(B\) \( \Rightarrow \angle BDA = \angle C = 30^\circ \) Chọn B.
Phần II. Tự luận: Bài 1: Phương pháp: a) Vận dụng tính chất kết hợp của phép nhân và phép cộng tính hợp lí. b) Tính lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\) Thực hiện các phép toán với các số hữu tỉ. c) Tính căn bậc hai. Thực hiện các phép toán với các số hữu tỉ. d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Thực hiện các phép toán với các số hữu tỉ. Cách giải: a) \(\left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\) \(\begin{array}{l} = \left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right).\dfrac{4}{5} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right).\dfrac{4}{5}\\ = \left( { - \dfrac{1}{5} + \dfrac{3}{7} + \dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right).\dfrac{4}{5}\\ = \left[ {\left( { - \dfrac{1}{5} + \dfrac{{ - 4}}{5}} \right) + \left( {\dfrac{3}{7} + \dfrac{4}{7}} \right)} \right].\dfrac{4}{5}\\ = \left( {\dfrac{{ - 5}}{5} + \dfrac{7}{7}} \right).\dfrac{4}{5}\\ = \left( { - 1 + 1} \right).\dfrac{4}{5}\\ = 0.\dfrac{4}{5} = 0\end{array}\) b) \(3.\sqrt {\dfrac{1}{9}} + 1,5.\sqrt {225} \) \(\begin{array}{l} = 3.\dfrac{1}{3} + \dfrac{3}{2}.15\\ = 1 + \dfrac{{45}}{2}\\ = \dfrac{2}{2} + \dfrac{{45}}{2}\\ = \dfrac{{47}}{2}\end{array}\) c) \(\left( { - 1,5} \right) + 2.\left| {2\dfrac{1}{2}} \right| - 6.\left| {\dfrac{{ - 16}}{3}} \right| + 5.\left| { - 0,3} \right|\) \(\begin{array}{l} = - 1,5 + 2.2\dfrac{1}{2} - 6.\left[ { - \left( {\dfrac{{ - 16}}{3}} \right)} \right] + 5.\left[ { - \left( { - 0,3} \right)} \right]\\ = - 1,5 + 2.\dfrac{5}{2} - 6.\dfrac{{16}}{3} + 5.0,3\\ = - 1,5 + 5 - 32 + 1,5\\ = \left( { - 1,5 + 1,5} \right) + \left( {5 - 32} \right)\\ = 0 + \left( { - 27} \right)\\ = - 27\end{array}\) Bài 2: Phương pháp: a) Thực hiện phép nhân hai số hữu tỉ, tìm \(x\). b) Thực hiện phép chia hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\) c) Tính căn bậc hai Vận dụng quy tắc chuyển vế tìm \(x\) d) \(\left| x \right| = a\) Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\) Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\) Cách giải: a) \(x:\left( { - \dfrac{3}{5}} \right) = 1\dfrac{1}{4}\) \(\begin{array}{l}x:\left( { - \dfrac{3}{5}} \right) = \dfrac{5}{4}\\x = \dfrac{5}{4}.\left( { - \dfrac{3}{5}} \right)\\x = \dfrac{{ - 3}}{4}\end{array}\) Vậy \(x = \dfrac{{ - 3}}{4}\) b) \({\left( {0,9} \right)^9}:x = - {\left( {0,9} \right)^7}\) \(\begin{array}{l}x = {\left( {0,9} \right)^9}:\left[ { - {{\left( {0,9} \right)}^7}} \right]\\x = - \left[ {{{\left( {0,9} \right)}^9}:{{\left( {0,9} \right)}^7}} \right]\\x = - {\left( {0,9} \right)^{9 - 7}}\\x = - {\left( {0,9} \right)^2}\\x = - 0,81\end{array}\) Vậy \(x = - 0,81\) c) \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \) Vì \(5 < 7\) nên \(\sqrt 5 < \sqrt 7 \) do đó, \(\sqrt 5 - \sqrt 7 < 0\) Vì \(\left| {x - 12} \right| \ge 0\) với mọi số thực \(x\) mà \(\sqrt 5 - \sqrt 7 < 0\) nên không có giá trị nào của \(x\) thỏa mãn \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \). Vậy \(x \in \emptyset \)
Bài 3: Phương pháp: a) Vận dụng kiến thức về hai tam giác bằng nhau: chứng minh \(\Delta ABD = \Delta AMD\left( {c.g.c} \right)\) b) Từ chứng minh a có \(\Delta ABD = \Delta AMD\left( {c.g.c} \right)\)suy ra được điều phải chứng minh của đề bài c) Vận dụng kiến thức về 2 góc bù nhau, suy ra \(\angle NBD = \angle CMD\) Vận dụng kiến thức về hai tam giác bằng nhau: chứng minh \(\Delta BND = \Delta MCD\left( {g.c.g} \right)\) d) Vận dụng tính chất của tam giác cân: đường phân giác trong tam giác cân cũng là đường cao của tam giác đó. Cụ thể chứng minh \(AD\) là đường cao của tam giác cân \(ABM \Rightarrow AD \bot BM\,\,\,\left( 1 \right)\). Chứng minh tương tự \(AD\) cũng là đường cao của tam giác cân \(ANC \Rightarrow AD \bot NC\,\,\left( 2 \right)\) Từ (1) và (2), suy ra \(BM//NC\) (quan hệ từ vuông góc đến song song) Cách giải:
a) Vì \(AD\) là tia phân giác của \(\angle BAC\) nên \(\angle BAD = \angle DAC\) Xét \(\Delta ABD\) và \(\Delta AMD\) có: \(\left. \begin{array}{l}AB = AM\\\angle BAD = \angle DAM\\AD\,chung\end{array} \right\} \Rightarrow \Delta ABD = \Delta AMD\left( {c.g.c} \right)\) b) Vì \(\Delta ABD = \Delta AMD\left( {cmt} \right) \Rightarrow \left\{ \begin{array}{l}AM = AB\\\angle ABD = \angle AMD\end{array} \right.\)(2 cạnh tương ứng và 2 góc tương ứng của hai tam giác bằng nhau) c) Ta có: \(\angle NBD + \angle ABD = {180^0}\) (2 góc kề bù) \(\angle CMD + \angle AMD = {180^0}\) (2 góc kề bù) Mà \(\angle ABD = \angle AMD\left( {cmt} \right)\) Suy ra \(\angle NBD = \angle CMD\) Xét \(\Delta BND\) và \(\Delta MCD\) có: \(\left. \begin{array}{l}\angle NBD = \angle CMD\left( {cmt} \right)\\BD = MD\left( {cmt} \right)\\\angle BDN = \angle MDC\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array} \right\} \Rightarrow \Delta BND = \Delta MCD\left( {g.c.g} \right)\) d) Xét \(\Delta ABM\) có \(AB = AM\left( {gt} \right)\) nên \(\Delta ABM\) cân tại \(A\). Lại có \(AD\) là phân giác của \(\angle BAM\) Suy ra \(AD\) là đường cao của \(\Delta ABM\) \( \Rightarrow AD \bot BM\,\,\,\left( 1 \right)\) Vì \(\Delta BND = \Delta MCD\left( {cmt} \right) \Rightarrow NB = CM\) (2 cạnh tương ứng) Lại có: \(B \in AN \Rightarrow AB + BN = AN\) \(M \in AC \Rightarrow AM + MC = AC\) Mà \(AB = AM;NB = CM\) Suy ra \(AN = AC\) Xét \(\Delta ANC\) có \(AN = AC\left( {cmt} \right)\) nên \(\Delta ANC\) cân tại \(A\). Lại có \(AD\) là đường phân giác \(\angle NAC\) Suy ra \(AD\) là đường cao của \(\Delta ANC\) \( \Rightarrow AD \bot NC\,\,\,\left( 2 \right)\) Từ (1) và (2), suy ra \(BM//NC\) (quan hệ từ vuông góc đến song song) (đpcm) Bài 4 Phương pháp: Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia, ta phải đổi dấu số hạng đó. Cách giải: Ta có: \(ab + a + b = 1 \Rightarrow ab = 1 - a - b\) \(\begin{array}{*{20}{l}}{ \Rightarrow {{\left( {ab} \right)}^2} = {{\left( {1 - a - b} \right)}^2} = \left( {1 - a - b} \right)\left( {1 - a - b} \right)}\\{\quad \quad \;\;\quad {\rm{ \;}} = 1 - a - b - a + {a^2} + ab - b + ab + {b^2}}\\{\quad \quad \quad \;\; = 1 + {a^2} + {b^2} + 2ab - 2a - 2b}\end{array}\) Lại có: \(\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right) = 1 + {a^2} + {b^2} + {a^2}{b^2}\) \(\begin{array}{*{20}{l}}{ = 1 + {a^2} + {b^2} + {{\left( {ab} \right)}^2}}\\{ = 1 + {a^2} + {b^2} + {{\left( {1 - a - b} \right)}^2}}\\{ = 1 + {a^2} + {b^2} + 1 + {a^2} + {b^2} + 2ab - 2a - 2b}\\{ = 2 + 2{a^2} + 2{b^2} + 2ab - 2a - 2b}\\{ = 2\left( {1 + {a^2} + {b^2} + ab - a - b} \right)}\\{ = 2\left( {{a^2} + {b^2} + 2ab} \right)}\\{ = 2{{\left( {a + b} \right)}^2}}\end{array}\) \( \Rightarrow \sqrt {2.\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)} {\rm{ \;}} = \sqrt {2.2{{\left( {a + b} \right)}^2}} {\rm{ \;}} = \sqrt {4{{\left( {a + b} \right)}^2}} {\rm{ \;}} = 2\left( {a + b} \right)\) (đpcm)
|




















Danh sách bình luận