Đề thi học kì 2 Toán 7 - Đề số 11 - Kết nối tri thứcTổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Phần trắc nghiệm (3 điểm) Em hãy chọn phương án trả lời đúng Câu 1: Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố: A. Chắc chắn B. Không thể C. Ngẫu nhiên D. Không chắc chắnĐề bài
I. Trắc nghiệm
Câu 1 :
Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố:
Câu 2 :
Chọn ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:
Câu 3 :
Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2. Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
Câu 4 :
Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
Câu 5 :
Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
Câu 6 :
Hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Câu 7 :
Cho ΔABC có: \(\widehat A = 3{5^0}\). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của \(\widehat {ACB} \). Số đo các góc \(\widehat {ABC}; \widehat {ACB} \)là:
Câu 9 :
Số đỉnh của hình hộp chữ nhật là:
Câu 10 :
Các mặt bên của hình lăng trụ đứng là:
Câu 11 :
Hãy chọn câu sai. Hình hộp chữ nhật ABCD. A'B'C'D' có:
Câu 12 :
Hình hộp chữ nhật có ba kích thước lần lượt là: a, 2a, \(\frac{a}{2}\) thể tích của hình hộp chữ nhật đó là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố:
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về biến cố. Lời giải chi tiết :
Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố ngẫu nhiên. Đáp án C.
Câu 2 :
Chọn ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:
Đáp án : A Phương pháp giải :
Xác định khả năng xuất hiện của biến cố. Lời giải chi tiết :
Trong 4 số trên, không có số nào chia hết cho 5. Do đó xác suất để chọn được số chia hết cho 5 là 0. Đáp án A.
Câu 3 :
Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2. Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
Đáp án : B Phương pháp giải :
Sử dụng quy tắc cộng hai đa thức Lời giải chi tiết :
h(x) = f(x) + g(x) = (5x4 + x3 – x2 + 1) + (–5x4 – x2 + 2) = 5x4 + x3 – x2 + 1 – 5x4 – x2 + 2 = (5x4 – 5x4) + x3 + (- x2 – x2) + (1 + 2) = x3 – 2x2 + 3 Bậc của h(x) là 3. Đáp án B.
Câu 4 :
Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về đa thức một biến. Lời giải chi tiết :
6x3 + 5x4 – 8x6 – 3x2 + 4 = - 8x6 + 5x4 + 6x3 – 3x2 + 4 Đáp án D.
Câu 5 :
Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
Đáp án : C Phương pháp giải :
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác. Lời giải chi tiết :
Vì AC > BC > AB nên \(\widehat B > \widehat A > \widehat C\) hay \(\widehat C < \widehat A < \widehat B\). Đáp án C.
Câu 6 :
Hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Đáp án : C Phương pháp giải :
Dựa vào kiến thức về đường xiên. Lời giải chi tiết :
"Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn". Đáp án C.
Câu 7 :
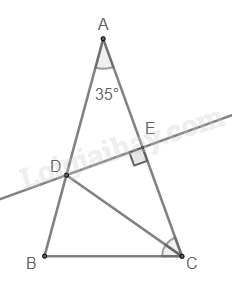
Cho ΔABC có: \(\widehat A = 3{5^0}\). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của \(\widehat {ACB} \). Số đo các góc \(\widehat {ABC}; \widehat {ACB} \)là:
Đáp án : C Phương pháp giải :
Dựa vào đặc điểm của đường trung trực. Sử dụng định lí tổng ba góc của một tam giác bằng \({180^0}\) Lời giải chi tiết :
Đường trung trực của AC đi qua điểm D nên tam giác ADC cân tại D. Do đó \(\widehat {DAC} = \widehat {DCA} = {35^0}\). Mà CD là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {ACB} = 2\widehat {DCA} = {2.35^0} = {70^0}\) Từ đó suy ra: \(\begin{array}{l}\widehat {ABC} = {180^0} - \widehat {BAC} - \widehat {BCA}\\ = {180^0} - {35^0} - {70^0} = {75^0}\end{array}\) Vậy \(\widehat {ABC} = 7{5^0}; \widehat {ACB} = 7{0^0}\). Đáp án C.
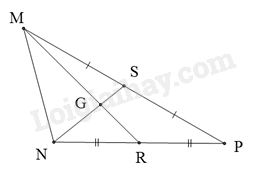
Đáp án : A Phương pháp giải :
Chứng minh MR là đường trung tuyến nên G là trọng tâm của tam giác để tính MR. Lời giải chi tiết :
Vì S là trung điểm của MP và R là trung điểm của NP nên MR và NS là hai đường trung tuyến của tam giác MNP. MR và NS cắt nhau tại G nên G là trọng tâm của tam giác MNP. Do đó \(MG = \frac{2}{3}MR\) suy ra \(MR = MG:\frac{2}{3} = 3:\frac{2}{3} = \frac{9}{2} = 4,5\left( {cm} \right)\) Đáp án A.
Câu 9 :
Số đỉnh của hình hộp chữ nhật là:
Đáp án : B Phương pháp giải :
Dựa vào đặc điểm của hình hộp chữ nhật. Lời giải chi tiết :
Hình hộp chữ nhật có 8 đỉnh. Đáp án B.
Câu 10 :
Các mặt bên của hình lăng trụ đứng là:
Đáp án : C Phương pháp giải :
Dựa vào đặc điểm của hình lăng trụ đứng. Lời giải chi tiết :
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật. Đáp án C.
Câu 11 :
Hãy chọn câu sai. Hình hộp chữ nhật ABCD. A'B'C'D' có:
Đáp án : A Phương pháp giải :
Dựa vào đặc điểm của hình hộp chữ nhật. Lời giải chi tiết :
Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh. Đáp án A.
Câu 12 :
Hình hộp chữ nhật có ba kích thước lần lượt là: a, 2a, \(\frac{a}{2}\) thể tích của hình hộp chữ nhật đó là:
Đáp án : D Phương pháp giải :
Dựa vào công thức tính thể tích hình hộp chữ nhật. Lời giải chi tiết :
Thể tích của hình hộp chữ nhật đó là: \(V = a.2a.\frac{a}{2} = {a^3}\). Đáp án D.
II. Tự luận
Phương pháp giải :
Dựa vào kiến thức về tỉ lệ thức: + Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\). + Nếu \(ad = bc\) (với \(a,b,c,d \ne 0\)) thì ta có các tỉ lệ thức: \(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{b}{a} = \frac{d}{c};\frac{c}{a} = \frac{d}{b}\). Lời giải chi tiết :
a) \(x:27 = -2:3,6\) \(\begin{array}{l}\frac{x}{{27}} = \frac{{- 5}}{9}\\x = \frac{{- 5.27}}{9}\\x = -15\end{array}\) Vậy \(x = -15\). b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\) \(\begin{array}{l}{\left( {2x + 1} \right)^2} = 81\\{\left( {2x + 1} \right)^2} = {9^2}\\\left[ \begin{array}{l}2x + 1 = 9\\2x + 1 = -9\end{array} \right.\\\left[ \begin{array}{l}2x = 8\\2x = -10\end{array} \right.\\\left[ \begin{array}{l}x = 4\\x = -5\end{array} \right.\end{array}\) Vậy \(x = 4\) hoặc \(x = - 5\). Phương pháp giải :
a) Sử dụng quy tắc thu gọn đa thức một biến. b) Chứng minh Q(x) không thể bằng 0. Lời giải chi tiết :
a) \(\begin{array}{l}Q(x) = - 3{x^4} + 4{x^3} + 2{x^2} + \frac{2}{3} - 3x - 2{x^4} - 4{x^3} + 8{x^4} + 1 + 3x\\ = \left( { - 3{x^4} - 2{x^4} + 8{x^4}} \right) + \left( {4{x^3} - 4{x^3}} \right) + 2{x^2} + \left( {3x - 3x} \right) + \left( {\frac{2}{3} + 1} \right)\\ = 3{x^4} + 2{x^2} + \frac{5}{3}\end{array}\) b) Ta có: \(\begin{array}{l}{x^4} \ge 0{\rm{ }}\forall x \Rightarrow 3{x^4} \ge 0{\rm{ }}\forall x\\{x^2} \ge 0{\rm{ }}\forall x \Rightarrow 2{x^2} \ge 0{\rm{ }}\forall x\\ \Rightarrow Q(x) = 3{x^4} + 2{x^2} + \frac{5}{3} \ge \frac{5}{3}{\rm{ }}\forall x\end{array}\) Vậy \(Q\left( x \right)\) không có nghiệm Phương pháp giải :
Kiểm tra khả năng xảy ra của biến cố. Lời giải chi tiết :
a) Không có số nào chia hết cho 5 nên xác suất để chọn được số chia hết cho 5 là 0. b) Cả 4 số đều là số có hai chữ số nên xác suất để chọn được số có hai chữ số là 1. c) Có hai số (11; 13) là số nguyên tố nên xác suất để chọn được số nguyên tố là \(\frac{2}{4} = \frac{1}{2}\). d) Có một số (12) chia hết cho 6 nên xác suất để chọn được số chia hết cho 6 là \(\frac{1}{4}\). Phương pháp giải :
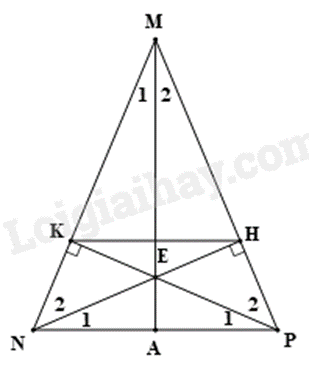
a) Chứng minh \(\Delta NHP = \Delta PKN\) theo trường hợp cạnh huyền – góc nhọn. b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta ENP\) cân. c) Chứng minh MK = MH. Chứng minh \(\Delta MEK = \Delta MEH\) (cạnh huyền – cạnh góc vuông) suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\). Do đó ME là đường phân giác của góc NMP. Lời giải chi tiết :
a) Xét \(\Delta NHP\) và \(\Delta PKN\) vuông tại H và K có: \(\widehat {NPH} = \widehat {PNK}\) (vì \(\Delta MNP\) cân tại M) \(NP\) chung Suy ra \(\Delta NHP = \Delta PKN\) (cạnh huyền – góc nhọn) (đpcm) b) Vì \(\Delta NHP = \Delta PKN\)nên \(\widehat {{N_1}} = \widehat {{P_1}}\). Do đó \(\Delta ENP\) cân tại E (đpcm) c) Ta có: \(MK = MN - NK\) (vì K thuộc MN) \(MH = MP - HP\) (vì H thuộc MP) Mà \(MN = MP\) (vì \(\Delta MNP\) cân tại M) \(NK = PH\) (vì \(\Delta NHP = \Delta PKN\)) suy ra \(MK = MH\). Xét \(\Delta MEK\) và \(\Delta MEH\) vuông tại K và H có: ME là cạnh chung MK = MH (cmt) Suy ra \(\Delta MEK = \Delta MEH\) (ch – cgv) Suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\) suy ra ME là tia phân giác của góc NMP (đpcm) Phương pháp giải :
Thay x = 1 vào đa thức P(x) để giải thích. Lời giải chi tiết :
Thay x = 1 vào đa thức P(x), ta có: P(1) = a.12 + b.1 + c = a + b + c Mà a + b + c = 0 Do đó, P(1) = 0. Như vậy x = 1 là một nghiệm của P(x) Phương pháp giải :
Tính diện tích phải sơn của một mặt tăng thêm. Gọi độ dài của chiếc hộp ban đầu là x. Sử dụng công thức tính diện tích hình vuông để viết biểu thức tìm x. Lời giải chi tiết :
Diện tích phải sơn một mặt của hình hộp tăng thêm là: 216: 6 = 36 (cm2) Gọi độ dài cạnh của hình hộp lập phương là x (cm) (x > 0) Diện tích phải sơn một mặt của hình hộp tăng thêm: \(\begin{array}{l}{\left( {x + 2} \right)^2} - {x^2} = 36\\{x^2} + 4x + 4 - {x^2} = 36\\4x + 4 = 36\\4x = 32\\x = 8\end{array}\) Vậy độ dài cạnh của chiếc hộp lập phương bằng 8 cm.
|
